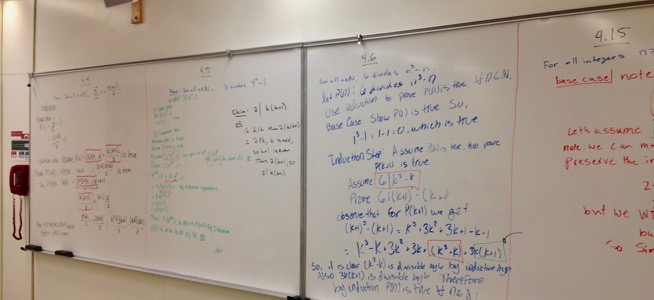| Week 15 |
|---|
|
[12.08.17] - Friday
A little introduction to cardinality.
|
|
Homework: Writing Assignment #12.
|
|
[12.06.17] - Wednesday
Lectured on the rest of inverse functions.
|
|
Homework: Keep working on Writing Assignment #12.
|
|
[12.04.17] - Monday
Great day with great discussions.
|
What we covered:
- At the board: 7.20, 7.23(a,b,c), 7.25, 7.26
|
|
Homework: Start working on Writing Assignment #12. Next time I will lecture on inverse functions and start on cardinality.
|
| Week 14 |
|---|
|
[12.01.17] - Friday
Best. Day. Ever. Tons of good conversation that culminated with a question, a conjecture, and a proof. And that, is what math is all about! Extra special thanks to HF and NH!!
|
What we covered:
- At the board: 7.8, 7.16(e,f), 7.19(a,c), Additional Problem #1
|
Homework 36 (Due Next Time):
- To turn in:
- Proofs/solutions (or your best efforts) for: 7.20, 7.21, 7.23, 7.25, 7.26
|
|
[11.29.17] - Wednesday
More one-to-one and onto
|
What we covered:
- At the board: 7.13(c,d), 7.16(c,d)
|
Homework 35 (Due Next Time):
- To turn in:
- Proofs/solutions (or your best efforts) for: 7.19 and Additional Problem #1: find a bijection from $[1,3]$ to $[2,10]$, where $[1,3]$ and $[2,10]$ are intervals of real numbers.
- Redo and turn in problems from last time: 7.8, 7.13(c,d), 7.15(a,b), 7.16(c,d,e,f).
- Hint:
- on the additional problem, your function should be something you can graph—think of lines.
|
|
[11.27.17] - Monday
Functions: one-to-one and onto
|
What we covered:
- At the board: 7.7, 7.13(a)(b), 7.15(c)(d), 7.16(a)(b)
|
Homework 34 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 7.8, 7.13(c,d), 7.15(a,b), 7.16(c,d,e,f).
- Clarification:
- in Exercise 7.16, make sure to either prove or provide a counterexample to support your answer. If you need to prove a property, please make it a formal (but perhaps short) proof.
|
| Week 13 |
|---|
|
[11.22.17] - Wednesday
Exam 2. Finished. Happy Thanksgiving!
|
Homework 33 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 7.7, 7.13(a)(b), 7.15(c)(d), 7.16(a)(b).
- Clarification:
- in Exercise 7.16, make sure to either prove or provide a counterexample to support your answer. If you need to prove a property, please make it a formal (but perhaps short) proof.
|
|
[11.20.17] - Monday
Functions
|
|
What we covered:
|
|
Exam 2 on Wednesday:
|
| Week 12 |
|---|
|
[11.17.17] - Friday
Even more modular arithmetic and divisibility by $3$.
|
What we covered:
- At the board: 6.80(a), 6.82, 6.83, 6.84
|
Homework 32 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 7.3, 7.5.
- Review: Also bring any questions you have about the material that will be on the exam. Concrete problems (from our notes or from the review sheet) are usually the best.
|
|
[11.15.17] - Wednesday
More modular Arithmetic.
|
What we covered:
- At the board: 6.70, 6.71, 6.72, 6.78, 6.79
|
Homework 31 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 6.80(a), 6.82, 6.83.
- Clarification: The point of 6.80 is that Definition 6.78 only tells you how to add or multiply two elements of $\mathbb{Z}/m\mathbb{Z}$ at a time. Now you want to add or multiply several at at time. Try using induction.
|
|
[11.13.17] - Monday
Modular Arithmetic.
|
What we covered:
- At the board: 6.52, 6.63, 6.64, 6.66, 6.69
|
Homework 30 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 6.70, 6.71, 6.72, 6.78. (You need to download the notes for Chapter 6 again to get the section on modular arithmetic.)
- Hint: On 6.78, first practice multiplying in $\mathbb{Z}/6\mathbb{Z}$. For example, $[2]_6\cdot [5]_6 = [10]_6$. Also, $[10]_6 = [4]_6$ since $10-4$ is divisible by $6$. Thus, $[2]_6\cdot [5]_6 = [4]_6$. Similarly, $[5]_6\cdot [5]_6 = [1]_6$; do you see why?
|
| Week 11 |
|---|
|
[11.08.17] - Wednesday
Partitions.
|
What we covered:
- At the board: 6.40(b), 6.44(g), 6.48, 6.49, 6.50
|
Homework 29 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 6.52, 6.63, 6.64, 6.66, 6.69. (You need to download the notes for Chapter 6 again to get the section on modular arithmetic.)
- Hint: On 6.64, translate what you want to prove into the language of divisibility, and then try to make use of the results you proved in Chapter 2.
|
|
[11.06.17] - Monday
Even more equivalence relations.
|
What we covered:
- At the board: I lectured over parts of 6.37, 6.41, 6.44, and 6.39
|
Homework 28 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 6.40(b), 6.44 - only part (g) of 6.32, 6.48, 6.49, 6.50.
- Hint: In Theorem 6.40(b), you want to prove an "or" statement. A typical way to prove "$P$ or $Q$" is as follows: if $Q$ is true, then the statement "$P$ or $Q$" is automatically true, so we may assume that $Q$ is false and then use that to show that $P$ is true. Thus, you may assume that $[x]\cap[y] \neq \emptyset$ and use that to prove that $[x]=[y]$. Now, if $[x]\cap[y] \neq \emptyset$, then there exists some $c\in A$ such that $c \in [x]$ and $c \in [y]$. What does that tell you? (Theorem 6.39 may be helpful.)
|
| Week 10 |
|---|
|
[11.03.17] - Friday
More Equivalence Relations.
|
What we covered:
- At the board: parts of parts of 6.37, 6.38, parts of 6.39
|
Homework 27 (Due Next Time):
- To turn in: Nothing!
- Reading: please (re)read from 6.33 through 6.44. You are high encouraged to work on 6.39, 6.40, and 6.44. I will use most of Monday's class to review these problems and introduce section 6.3.
|
|
[11.01.17] - Wednesday
Equivalence Relations.
|
What we covered:
- At the board: parts of 6.27, 6.30, parts of 6.32, parts of 6.37
|
Homework 26 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 6.36, 6.37, 6.38, 6.39.
- Clarification:
- Please redo 6.37 even if you completed it before. Also a hint: the answer to "How many different sets of relatives are there?" is a number between 1 and 10.
- I will only grade your effort on 6.39, so please give it your all.
|
|
[10.30.17] - Monday
Relations.
|
What we covered:
- At the board: 6.20, 6.25, 6.26, parts of 6.27
|
Homework 25 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 6.30, 6.32, 6.37. Also, you may redo Homework 24 (or just turn in what you had from last time)
- Hint:
- Read the directions for Exercise 6.32; make sure to use (and reference) your answers to 6.27.
|
| Week 9 |
|---|
|
[10.27.17] - Friday
Irrationality of $\sqrt{p}$ and relations.
|
What we covered:
- At the board: 5.17, 6.8, 6.9, 6.13, 6.19
|
Homework 24 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 6.20, 6.25, 6.26, 6.27
- Hint:
- Read and reread Definition 6.23. Does Example 6.24 make sense?
- Here are more details Example 6.24(a). You know $1 \lt 2$ but $2 \nless 1$, so this example proves (via a counterexample) that $\lt$ is not symmetric. You also know that $1 \nless 1$, so $\lt$ is not reflexive. However, it is true that for all $x,y,z\in \mathbb{R}$, if $x\lt y$ and $y\lt z$ then $x \lt z$; this proves that $\lt$ is transitive.
|
|
[10.25.17] - Wednesday
Irrationality of $\sqrt{2}$ and the Well-Ordering Property.
|
|
What we covered:
|
Homework 23 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 5.17, 6.8, 6.9, 6.13, 6.19
- Clarification:
- In proving Theorem 5.17, you are free to use theorems from section 5.1, even if we didn't prove them. Theorem 5.12 will probably be useful.
- For 6.13, you want to imagine the sets lying in $\mathbb{R} \times \mathbb{R}$, where the first coordinate is the $x$-coordinate and the second is the $y$-coordinate. Your answers could be given in words and/or pictures.
|
|
[10.23.17] - Monday
More complete induction
|
What we covered:
- At the board:4.20, 4.27, 4.29
|
Homework 22 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 5.16, 6.5, 6.6
- Reading : Please read Theorem 4.3.4 about the Well-Ordering Principle. Also, make sure to read the beginning of Section 5.2 before starting 5.16.
- Clarification:
- For Theorem 5.16, I will only grade whether or not you thought about it. Make sure to write down your ideas! Also, make sure to read the footnote for the theorem.
- I will be giving a mini-lecture on the Well-Ordering Principle after we discuss the problems to turn in.
|
| Week 8 |
|---|
|
[10.20.17] - Friday
More Induction, and intro. to complete induction
|
What we covered:
- At the board:4.16, 4.19, 4.22
|
Homework 21 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 4.20, 4.27, 4.29
- Hint:
- If you get stuck on any of these, make sure to clearly outline your proof by induction and carefully check the base case (called the base step in the notes).
|
|
[10.18.17] - Wednesday
More Induction.
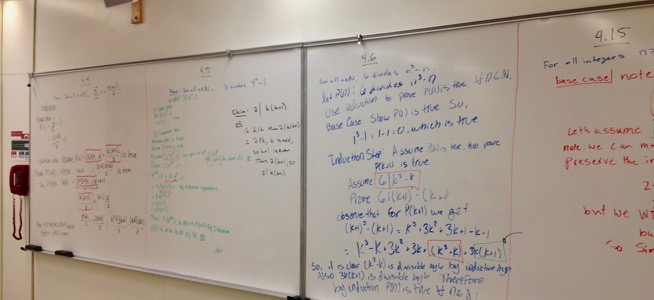
- Rainbow induction. -
|
What we covered:
- At the board:4.4, 4.5, 4.6, 4.15
|
Homework 20 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 4.16, 4.19, 4.22
- Hint:
- If you get stuck on any of these, make sure to clearly outline your proof by induction and carefully check the base case (called the base step in the notes).
|
|
[10.16.17] - Monday
Induction.
|
What we covered:
- At the board:Extra Problem #1, 4.13
|
Homework 19 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 4.4, 4.5, 4.6, 4.15
- Hint:
- If you get stuck on any of these, make sure to clearly outline your proof by induction and carefully check the base case (called the base step in the notes).
|
| Week 7 |
|---|
|
[10.13.17] - Friday
Unions and intersections and the beginning of induction.
|
What we covered:
- At the board:3.26, 3.39
- Mini-lecture:Introduction to induction (to be continued...)
|
|
Homework 18 (Due Next Time):
|
|
[10.11.17] - Wednesday
Big unions and intersections.
|
What we covered:
- At the board:3.27, 3.37, 3.38, 3.41, 3.42
|
Homework 17 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 3.26, 3.39, meditations on 4.4
- Reading : Make sure to read and reread section 4.1 up through problem 4.4. This is really important!
- Clarification:
- For Theorem 4.4, I will only grade whether or not you thought about it. Please make sure to come with lots of questions!
- I will be giving a mini-lecture on induction after we deal with 3.26 and 3.39.
|
|
[10.09.17] - Monday
Back to set theory.
|
What we covered:
- At the board:3.21(b), 3.25, 3.28, 3.35, 3.36
|
Homework 16 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 3.27, 3.37, 3.38, 3.41, 3.42
- Hint:
- Make sure to (re)read all of the text at the beginning of Section 3.3.
- More Reading (same as last time): The text between Problem 3.28 and Problem 3.31. Then meditate on the following problem: if $U$ is the collection of all sets and $S = \{A\in U\mid A\notin A\}$, then which is true: $S\in S$ or $S\notin S$?
|
| Week 6 |
|---|
|
[10.06.17] - Friday
Exam 1. Done.
|
|
What we covered:
|
Homework 15 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 3.21(b), 3.28, 3.35, 3.36
- Hint:
- Make sure to read all of the text at the beginning of Section 3.3 before starting 3.35.
- More Reading: The text between Problem 3.28 and Problem 3.31. Then meditate on the following problem: if $U$ is the collection of all sets and $S = \{A\in U\mid A\notin A\}$, then which is true: $S\in S$ or $S\notin S$?
|
|
[10.04.17] - Wednesday
The power set.
|
What we covered:
- At the board:3.20(a), 3.21(a), 3.25 (half of it)
|
|
Exam 1 on Friday:
|
|
[10.02.17] - Monday
The power set.
|
What we covered:
- At the board:3.20(a) - started
|
Homework 14 - Take 2 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 3.20(a), 3.21(a), 3.23, 3.25
- Clarification:
- This is an opportunity to completely redo the problem set from last time. Don't for get to start preparing for the exam too!
|
| Week 5 |
|---|
|
[09.29.17] - Friday
More set theory.


- Proving theorems. -
|
What we covered:
- At the board: 3.16, 3.17, 3.19
|
Homework 14 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 3.20(a), 3.21(a), 3.23, 3.25
- Clarification:
- For Problem 3.25, I will only grade you on effort (for now). Please make sure to try hard on it, come with lots of questions, and be ready to present what you have.
|
|
[09.27.17] - Wednesday
Starting basic set theory.
|
What we covered:
- At the board: 3.4, 3.5, 3.9, 3.10, 3.15
|
Homework 13 (Due Next Time):
- To turn in: Proofs/solutions (or your best efforts) for: 3.16, 3.17, 3.19
- Clarification:
- The sets in 3.16, are intervals of real numbers. Try to write your answers to this exercise in interval notation or using set-builder notation.
- Your goal in 3.17 is to prove $B^c\subseteq A^c$. So, using the hypothesis, you want to prove that for all $x\in B^c$, it follows that $x\in A^c$. As such, your proof should begin with "Let $x\in B^c$" and end with "Thus, $x\in A^c$."
- Before proving Theorem 3.19, make sure to read the text right before it. Your proof should have two parts (visually, two paragraphs). In one part you prove $A\setminus B \subseteq A \cap B^c$, and in the other part you prove $A \cap B^c \subseteq A\setminus B$.
|
|
[09.25.17] - Monday
Evaluating the truth of quantified statements.
|
What we covered:
- In groups: 2.69-2.80
- At the board: 2.69, 2.79, 2.80
|
Homework 12 (Due Wednesday):
- To turn in: Proofs/solutions (or your best efforts) for: 3.4, 3.5, 3.9, 3.10, 3.15
- Clarification:
- To clarify the directions for 3.4, here are two possible answers for part (a). Answer 1: $A = \{3,6,9,12,\ldots\}$. Answer 2: $A$ is the set of all natural numbers that are divisible by $3$.
- For 3.9, you should find that there are 8 different subsets.
- Before proving Theorem 3.10, make sure to read the text before Problem 3.7. Your goal in 3.10 is to prove $A\subseteq C$. So, using the additional hypotheses, you want to prove that for all $x\in A$, it follows that $x\in C$. As such, your proof should begin with "Let $x\in A$" and end with "Thus, $x\in C$."
|
| Week 4 |
|---|
|
[09.22.17] - Friday
Negating quantifiers.
|
What we covered:
- In groups: 2.68-2.74
- At the board: 2.68, 2.73, 2.74
|
Homework 11 (Due Monday):
- To turn in: Proofs/solutions (or your best efforts) for: 2.79, 2.80
- Clarification:
- There is a small something missing in the statement of Theorem 2.80. It should read "For all integers $n$, $3n^2 + n +14$ is even."
- The sentence before Theorem 2.80 suggests considering two cases. So, if you are having trouble proving the theorem all at once, try splitting your proof into two case: when $n$ is even and when $n$ is odd.
|
|
[09.20.17] - Wednesday
More quantifiers.
|
What we covered:
- In groups: 2.61-2.67
- At the board: 2.65, 2.66, 2.67
|
Homework 10 (Due Friday):
- To turn in: Proofs/solutions (or your best efforts) for: 2.68, 2.69, 2.73, 2.74
- Hint:
- Make sure to read (and reread) all of the words between the exercises. The ones between 2.73 and 2.74 are quite important.
- Again and again, quantifiers can be tricky; we will talk even more about these in class.
Remember, if you use any resources other than our notes and each other, you need to write these on the top of your homework. (See the syllabus for more details.)
|
|
[09.18.17] - Monday
Contradiction and quantifiers.

- Rainbow math -
|
What we covered:
- In groups: 2.55-2.62
- At the board: 2.55, 2.57, 2.58, 2.60
|
Homework 09 (Due Wednesday):
- To turn in: Proofs/solutions (or your best efforts) for: 2.63, 2.65, 2.66, 2.67
- Hint:
- Make sure to read (and reread) all of the words between the exercises.
- Again, quantifiers can be tricky; we will talk more about these in class.
Remember, if you use any resources other than our notes and each other, you need to write these on the top of your homework. (See the syllabus for more details.)
|
| Week 3 |
|---|
|
[09.15.17] - Friday
Contrapositive, Vader, and Palin.
|
What we covered:
- In groups: 2.43-2.52
- At the board: 2.43, 2.44, 2.45, 2.46, 2.48, 2.51
|
Homework 08 (Due Monday):
- To turn in: Proofs/solutions (or your best efforts) for: 2.55, 2.57, 2.58, 2.60, 2.61, 2.62,
- Hint:
- Remember to read the sentence right before 2.55. This is likely your first exposure to proof by contradiction. Read 2.53 and 2.54 carefully, but definitely come with questions on Monday.
- Also, be aware that quantifiers can be tricky, and the order in which they occur is extremely important.
Remember, if you use any resources other than our notes and each other, you need to write these on the top of your homework. (See the syllabus for more details.)
|
|
[09.13.17] - Wednesday
More Logic. Had great discussion about the contrapositive and negating conjunctions.
|
What we covered:
- In groups: 2.25-2.32
- At the board: 2.35, 2.36, 2.38, 2.41
|
Homework 07 (Due Friday):
- To turn in: Proofs/solutions (or your best efforts) for: 2.43, 2.44, 2.45, 2.46, 2.48, 2.51,
- Hint:
- Remember that the negation of "$x$ and $y$ are odd" is "$x$ or $y$ is even." Similarly, the negation of "$x$ or $y$ is even" is "$x$ and $y$ are odd."
- To do Exercises 2.48(b), you can use Corollary 2.47 (even though you are not ask to prove it).
Remember, if you use any resources other than our notes and each other, you need to write these on the top of your homework. (See the syllabus for more details.)
|
|
[09.11.17] - Monday
Logic.
|
What we covered:
- In groups: 2.25-2.32
- At the board: 2.28, 2.31
|
Homework 06 (Due Wednesday):
- To turn in: Proofs/solutions (or your best efforts) for: 2.34, 2.35, 2.36, 2.38, 2.40, 2.41, 2.43
- Hint: Read the sentence before Theorem 2.34. You can prove that two propositions are logically equivalent by constructing truth tables for each one and showing that they are the same. But, make sure to use your words like "consider the following truth tables" or "since the columns for $\neg(A\wedge B)$ and $\neg A \vee \neg B$ are identical..."
Remember, if you use any resources other than our notes and each other, you need to write these on the top of your homework. (See the syllabus for more details.)
|
| Week 2 |
|---|
|
[09.08.17] - Friday
You all. Are. Awesome.
|
What we covered:
- In groups: 2.21-2.25
- At the board: 2.18, 2.19, 2.22, 2.23
|
Homework 05 (Due Monday):
- Reading: Appendix C: Definitions in Mathematics
- To turn in: Proofs/solutions (or your best efforts) for: 2.25, 2.27, 2.28, 2.31, 2.32
- Challenge (but not for credit): Look at Theorem 2.23 again. Let's try to generalize it. Is it true that the for all $n\ge 2$, the sum of $n$ integers is divisible by $n$? If so, prove it. If not, can you determine for which values for $n$ it is true? (For example, Theorem 2.23 says that the statement is true when $n=3$, and it's also not hard to prove that it's true for $n=2$.)
Remember, if you use any resources other than our notes and each other, you need to write these on the top of your homework. (See the syllabus for more details.)
|
|
[09.06.17] - Wednesday
Another complete-sentences day with several good discussion surrounding this. Four stellar presentations by PA, JE$_1$, SK, and VT, and many comments from the rest. I'm loving it! ...hope you are too ☺

- So much beautiful math! -
|
What we covered:
- In groups: 2.14, 2.15, 2.16, 2.17, 2.18, 2.19, 2.20
- At the board: 2.14, 2.15, 2.16, 2.17
|
|
Homework 04 (Due Friday):
|
| Week 1 |
|---|
|
[09.01.17] - Friday
Ramped up the math today, and had the first (of many) complete-sentences day. We were treated to five outstanding presentations by AL, AK, DL, PC, and AF, and quite a few people chimed in to create some nice discussions. Great job all around! And my apologies to AF for the rush at the end! Here are a few photos—sorry AL, the picture of your proof was super blurry ☹



- We do math here! -
|
What we covered:
- In groups: 2.7, 2.8, 2.9, 2.12, 2.13
- At the board: 2.7, 2.8, 2.9, 2.12, 2.13
|
|
Homework 03 (Due Wednesday):
|
|
[08.30.17] - Wednesday
Yay math! Three great presentations today by HF, NS, and CE! There were lots of excellent talking points—many thanks for their patience and bravery as we talked through the details. And many thanks to the rest of the class for such a high level of participation on just the second day of class.
|
What we covered:
- In groups: 2.3-2.7
- At the board: 2.3, 2.4, 2.5
|
Homework 02 (Due Friday):
- Reading: Appendix A: Elements of Style for Proofs: the beginning through item 10 (i.e. the first two pages)
- To turn in:
- Short paragraph addressing one item from your reading from Appendix A that you had not though about before and/or did not think was important.
- Proofs of (or your best effort to prove) Problems 2.7, 2.8, 2.9, 2.12, 2.13 (from Chapter 2 of the course book)
|
|
[08.28.17] - Monday - First day!
Great to meet you all! Make sure to sign up for a ShareLaTeX account and get started on Writing Assignment 01. It's due this coming Friday!
|
|
What we covered: Setting the Stage (see the slides)
|
Homework 01 (Due Wednesday):
- Reading: Sections 1.1-1.3 of the course book
- To turn in:
- Short paragraph about one aspect of an IBL approach that you view as positive and one concern that you have.
(This is based off of the 1.1-1.3 reading.)
- Proofs of (or your best effort to prove) Theorem 2.3 and Theorem 2.4 (from Chapter 2 of the course book)
|