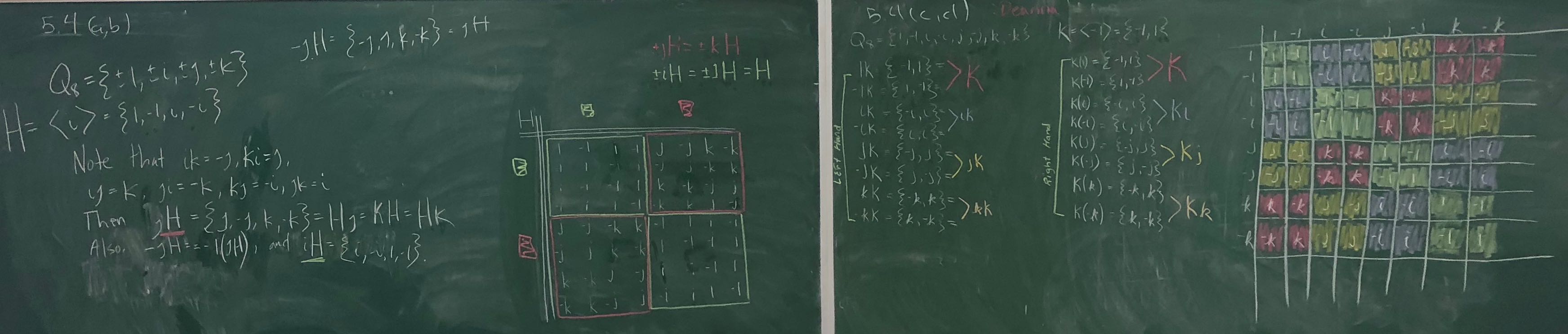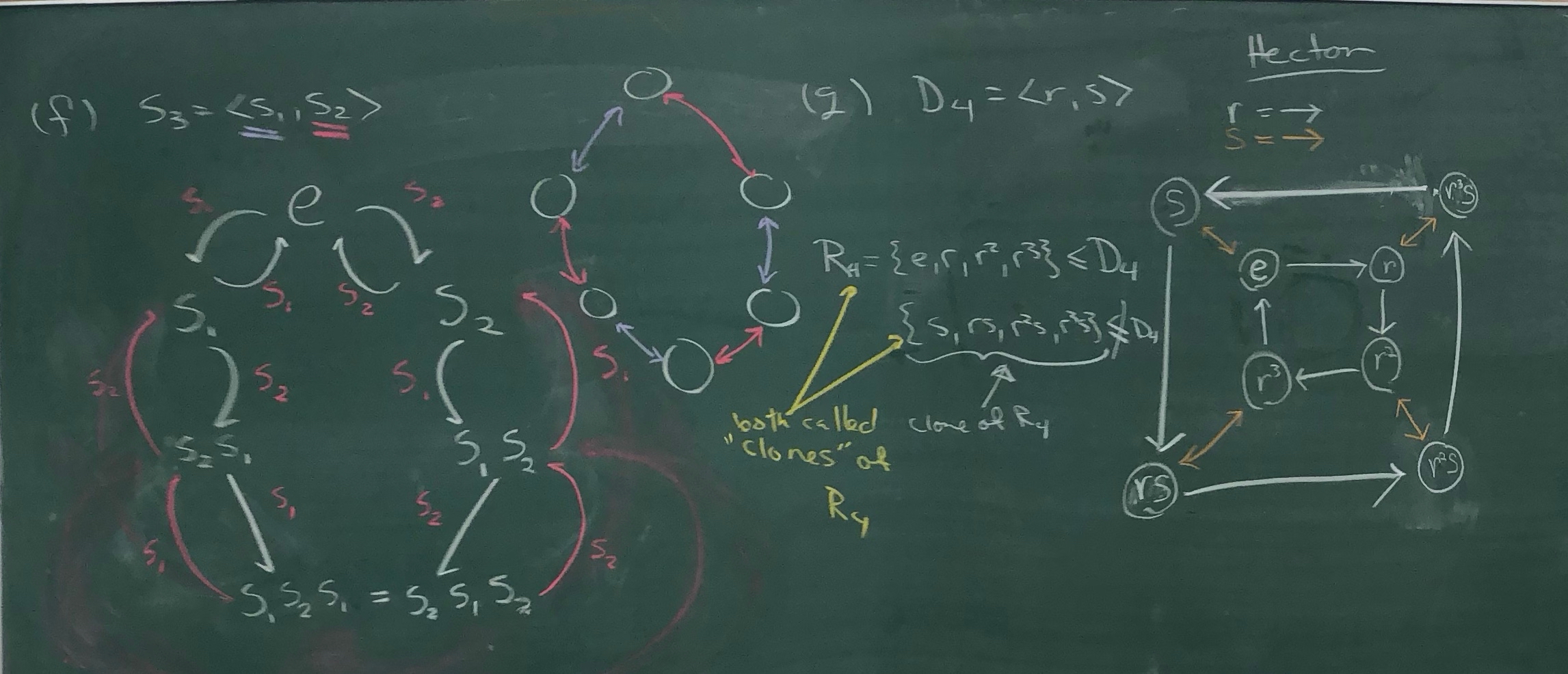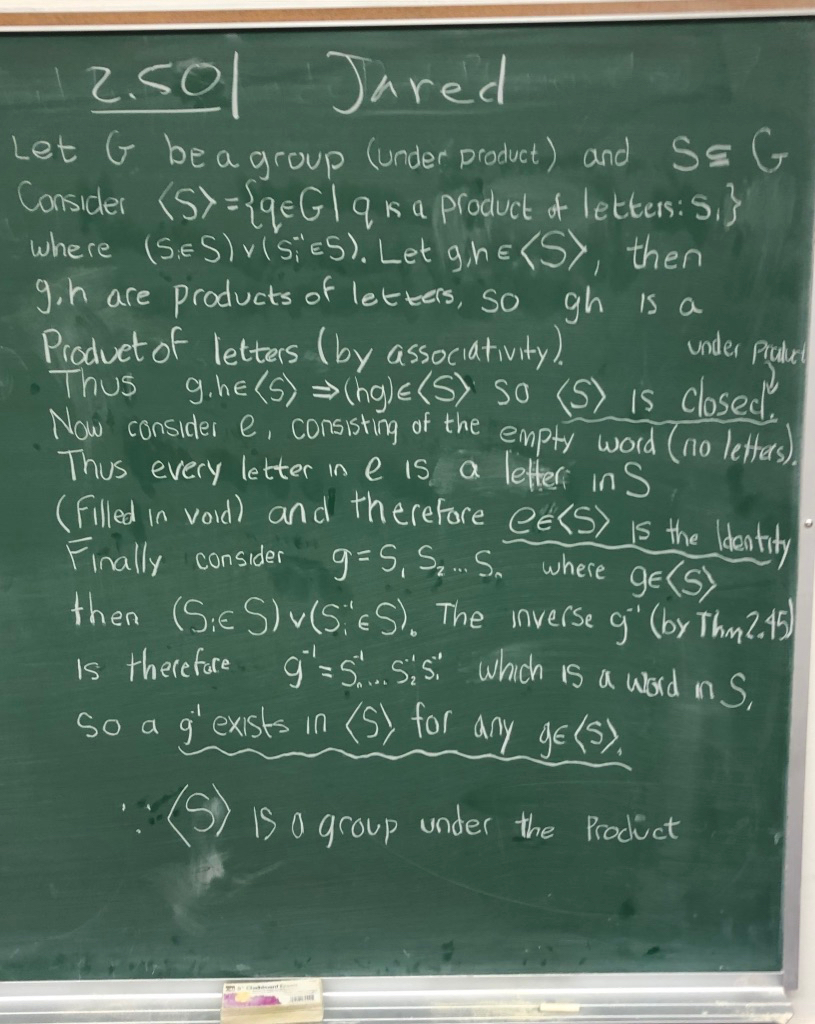الجبر
الجبر (al-jabr) roughly means to "restore" or "complete" and is from the title of the book Al-kitāb al-mukhtaṣar fī ḥisāb al-ğabr wa’l-muqābala by Muḥammad ibn Mūsā al-Khwārizmī (circa 820 CE)
Announcements
The final writing assignment Writing Assignment is due Friday 5/10. An outline for the final exam can be found below in the Other Handouts section of the webpage.
Meeting times: T,R 10:30
Office Hours: T,Th 9:30
Student grades are maintained on Canvas.
The Book
We are using a version of An Inquiry-Based Approach to Abstract Algebra, by Dana C. Ernst.
IBL-AbstractAlgebra.pdf
Daily Homework
Homework 27 (Due Thursday 5/09)
- Read: Continue with 7.1 and start 7.2
- Turn in: 7.3, 7.6, 7.7, 7.13, 7.15(a,b), 7.19, 7.21, 7.23, 7.24
- To try but not turn in: 7.19, 7.20, 7.22
Note that 7.6 and 7.7 should be short. You just need to connect a few things together, 7.5(c) and Lagrange's Theorem being the most important pieces for 7.6 and Corollary 4.25 for 7.7. For 7.7, if $|g| = m$, then you know that $g^m = e$ (and that $m$ is the smallest positive integer with this property); if you're stuck, try applying $\phi$ to both sides...
7.13 is an important theorem. Showing that "$\phi$ one-to-one $\implies$ $\operatorname{ker}(\phi) = \{e_1\}$" should follow quickly from the definition of the kernel. To prove "$\operatorname{ker}(\phi) = \{e_1\}$ $\implies$ $\phi$ one-to-one", you should begin by assuming that $\phi(x) = \phi(y)$ (and you want to show $x=y$). To make use of your hypothesis that $\operatorname{ker}(\phi) = \{e_1\}$, try manipulating the equation $\phi(x) = \phi(y)$ to get the identity on one side.
On 7.15, the idea is that if you know that $\phi(i)= h$ and $\phi(j) = v$, then, for example, you can figure out $\phi(k) = \phi(ij) = \phi(i)\phi(j)=\cdots$.
For 7.21, 7.23, 7.24, you are trying to show $G/N\cong H$ for different choices of $G$, $N$, and $H$. This can easily be done with the First Isomorphism Theorem by following these steps: (1) define a homomorphism $\phi:G \rightarrow H$ (unless it's already defined for you), (2) show that the image of $\phi$ is $H$, and (3) show that the kernel is $N$. Once you've done that, the First Isomorphism Theorem tells you that $G/N\cong H$.
Homework 26 (Due Tuesday 5/07)
- Read: Continue with 6.1 and 6.2. Start 7.1
- Turn in: 6.16, 6.19, 6.32(d), 6.38, 6.39, 7.2, 7.4, 7.5(c), 7.9, 7.10, 7.11
- To try but not turn in: 6.24, 6.41, 7.3, 7.6, 7.7
For 6.16, you can just use 6.15 (and 6.13).
In 6.39, you are assuming that $G$ is cyclic, and want to prove that $G/H$ is cyclic. One approach is to try to guess a generator for $G/H$, and then show that it works. If you guess that $aH$ is a generator (for a clever choice of $a$), you then need to show that for any $xH \in G/H$, $xH = (aH)^k$ for some $k\in \mathbb{Z}$.
If you find it hard to start 7.5(c), just carefully start applying the two-step subgroup test. You are free to use 7.5(a,b), even though I did not ask you to prove them. When working with $\phi(H)$, remember that it is just a set were the elements have a certain form: $x\in \phi(H) \iff x = \phi(h)$ for some $h\in H$.
For 7.11, there are two things to prove: (1) $\ker(\phi)$ is a subgroup, and (2) $a\ker(\phi) = \ker(\phi)a$ for all $a\in G$.
Homework 25 (Due Thursday 5/02)
- Read: Continue with 5.3, and start 6.1, start 6.2.
- Turn in: 5.21, 5.33, 6.9, 6.11, 6.12, 6.13 6.28, 6.32(a,b,c), 6.36
- To try but not turn in: 5.24, 5.37, 6.33
I did 5.21 in class, but I want you to write it up in your words; remember that 5.19 was very helpful in proving it.
Let me clarify 5.33. Let's name the subgroups: $A = \langle s \rangle$, $B = \langle r^2, sr^2\rangle$. To show $A\trianglelefteq B$, you need to show $bA = Ab$ for every $b\in B$; however, if you see that 5.32 applies (wink, wink), you can use that. Next, you should explain why $B \trianglelefteq D_4$. Finally, to show $B\not\trianglelefteq D_4$, you only need to find one element $g\in D_4$ such that $gB \neq Bg$.
Theorem 6.10 will be very helpful in proving 6.13; remember that $\operatorname{lcm}(a,b) = ab \iff \gcd(a,b) = 1$.
My recommendation for 6.32(a,b,c) is to first write out the left cosets of $\langle r \rangle$ in $D_4$, $\langle -1 \rangle$ in $Q_8$, and $\langle 4 \rangle$ in $\mathbb{Z}_{12}$. Then, in the first case, start computing the cosets $s\langle r \rangle, s^2\langle r \rangle,\ldots$ until you get the coset $\langle r \rangle$, which is the identity in the quotient group. In the second case, compute the cosets $j\langle -1 \rangle, j^2\langle -1 \rangle,\ldots$ until you get the coset $\langle -1 \rangle$, and in the third case, compute $5 + \langle 4 \rangle, 2\cdot 5 + \langle 4 \rangle, 3\cdot 5 + \langle 4 \rangle,\ldots$ until you get the coset $\langle 4 \rangle$, which is the identity in this quotient group.
Homework 24 (Due Tuesday 4/30)
- Read: Continue with 5.3, and start 6.1, start 6.2.
- To look over but not turn in
(oops...this was a mistake. I wanted you to turn these in) : 5.21, 5.25, 5.30, 5.33, 5.35, 6.6, 6.7, 6.27, 6.32(b,c) - Turn in: 6.26
I did 5.21 in class, but I want you to write it up in your words; remember that 5.19 was very helpful in proving it.
Let me clarify 5.33. Let's name the subgroups: $A = \langle s \rangle$, $B = \langle r^2, sr^2\rangle$. To show $A\trianglelefteq B$, you need to show $bA = Ab$ for every $b\in B$; however, if you see that 5.32 applies (wink, wink), you can use that. Next, you should explain why $B \trianglelefteq D_4$. Finally, to show $B\not\trianglelefteq D_4$, you only need to find one element $g\in D_4$ such that $gB \neq Bg$.
Before starting 6.6, please read the beginning of section 6.1, but the text between Theorem 6.5 and Problem 6.6 may be the most helpful. Similarly, please read the beginning of section 6.2 before starting 6.27 and 6.32. My recommendation for 6.32(b,c) is to first write out the left cosets of $\langle -1 \rangle$ in $Q_8$ and $\langle 4 \rangle$ in $\mathbb{Z}_{12}$. Then, in the first case, start computing the cosets $j\langle -1 \rangle, j^2\langle -1 \rangle,\ldots$ until you get the coset $\langle -1 \rangle$, which is the identity in the quotient group. In the second case, compute the cosets $5 + \langle 4 \rangle, 2\cdot 5 + \langle 4 \rangle, 3\cdot 5 + \langle 4 \rangle,\ldots$ until you get the coset $\langle 4 \rangle$, which is the identity in this quotient group.
Homework 23 (Due Tuesday 4/23)
- Read: Continue with 5.2, and start 3.3.
- To look over but not turn in: 5.19, 5.21, 5.22, 5.24, 5.30, 5.32, 5.35, 5.37
- Turn in: none
Please try to look over all of the problems listed above, but please focus on synthesizing the material and preparing for the exam.
Homework 22 (Due Thursday 4/18)
- Read: Start 4.4, and start 5.1. (We'll come back to the end of 4.3...hopefully...)
- Turn in: 4.110, 4.111 (just $S_6$ and $A_6$), 4.112, 5.5, 5.6, 5.7, 5.12, 5.14(a,b), 5.17
- To try but not turn in: 5.8, 5.9, 5.10, 5.11
For 4.111, you'll want to use 4.80 and 4.104. For 5.7, there will be only finitely many cosets, but each coset will be infinite.
Please carefully read over 5.9–5.11, but I will make sure to discuss them in class. One extremely important thing to take away, which is not so obvious, is that 5.9 and 5.10 imply that $$aH = bH \iff a^{-1}b\in H \iff b^{-1}a \in H.$$ You are welcome to use this!
Note that you will not need to use any of the previous results to prove 5.12; just work through the definitions of one-to-one and onto. For 5.17; just use 5.16.
Homework 21 (Due Tuesday 4/16)
- Read: Start 4.4, and start 5.1. (We'll come back to the end of 4.3...hopefully...)
- Turn in: 4.97, 4.101, 4.102, 4.103, 4.104, 4.108, 4.109(you do not have to draw the lattice), 5.2, 5.4
- To try but not turn in: 4.105, 4.107, 5.3
Please start by reading 4.90 and 4.91, which summarize our work with transpositions thus far. When thinking about 4.105, you want to imagine a permutation $\sigma$ that is a product of several disjoint cycles, say $\sigma = \sigma_1\sigma_2\cdots\sigma_m$. You can apply your answer from 4.104 to each of the cycles $\sigma_i$, and now you just need to figure out what that means for $\sigma$. On 4.108, $A_3$ is simply the list of permutations you wrote down in 4.101, and this should be a familiar subgroup of $S_3$.
When meditating on 4.107, you need to show that $A_n$ is a group and that it has order $n!/2$. To show that $|A_n| = n!/2$, remember that $|S_n| = n!$, so you need to show that half of all permutations from $S_n$ are in fact in $A_n$, which is to say that half of the permutations are even (and half are odd). We are not working with the integers, so this requires a different proof. Here's one idea. (Spoiler alert!) Let $\tau$ be any transposition in $S_n$ (for example $\tau = (1,2)$ would be fine). Define a function $\phi:S_n \rightarrow S_n$ by $\phi(\sigma) = \tau\sigma$. Now show that $\phi$ maps even permutations to odd permutations and vice versa. Also, show that $\phi$ is a bijection. Then tie it all together to show that the number of even permutations and the number of odd permutations in $S_n$ must be the same.
Before starting 5.2, make sure to read the example on page 69 a couple of times. Also, to help you check your work, here's the beginning of the computation for 5.4. In 5.4, the group is $Q_8$ one of the subgroups is $H = \langle i \rangle = \{1,-1,i,-i\}$. To compute the left cosets of $H$ in $Q_8$, we take individual elements of $Q_8$ and multiply $K$ on the left by them. (Remember: $ij = k$, $ji = -k$, $ik = -j$, $ki = j$, $jk=i$, $kj = -i$.)
- $1H = \{1\cdot1,1\cdot(-1), 1\cdot i, i\cdot (-i)\} = \{1,-1, i, -i\} = H$
- $-1H = $ (you do it)
- $iH = \{i\cdot1,i\cdot(-1), i\cdot i, i\cdot (-i)\} = \{i,-i, -1, 1\} = H$
- $-iH = $ (you do it)
- $jH = \{j\cdot1,j\cdot(-1), j\cdot i, j\cdot (-i)\} = \{j,-j, -k, k\}$
- $-jH = $(you do it)
- $kH = $(you do it)
- $-kH = \{(-k)\cdot1,(-k)\cdot(-1), (-k)\cdot i, (-k)\cdot (-i)\} = \{-k,k,-j, j\} = jH$
Homework 20 (Due Thursday 4/11)
- Read: Continue with 4.3.
- Turn in: 4.73, 4.74(a,b,e,f,g,k,l), 4.76, 4.78, 4.81, 4.82, 4.87, 4.88
- To try but not turn in: 4.74(the remaining parts), 4.75, 4.79, 4.80, 4.86
For 4.74, remember that when computing the composition $\alpha\gamma$, you should work from right to left: $\alpha\gamma(1) = \alpha(\gamma(1))$. However, when reading cycle notation, you always read left to right—confusing, right!?
On 4.76, you want to show that $\alpha\beta=\beta\alpha$ for arbitrary disjoint cycles $\alpha$ and $\beta$ in $S_n$. To do this, it can be useful to think of the permutations as functions. Thus, $\alpha\beta=\beta\alpha$ if and only if $\alpha\beta$ and $\beta\alpha$ have the same output for every input, i.e. if and only if $\alpha\beta(i)=\beta\alpha(i)$ for every $1\le i\le n$. For 4.82, you can just use 4.80.
Before starting 4.87, you should read the text before it, including Problem 4.86. Problem 4.86 gives an example of what you are trying to do: $(1,2,3)$ can be written as a product of transpositions as $(1,2,3) = (1,2)(2,3)$, but note that there a many possible ways to do this. Here's another: $(1,2,3) = (1,3)(1,2)$.
Homework 19 (Due Tuesday 4/9)
- Read: 4.2 and start 4.3.
- Turn in: 4.49, 4.53, 4.54, 4.64, 4.66, 4.68, 4.70, 4.72
- To try but not turn in: 4.67, 4.69, 4.71
For 4.49, 4.53, and 4.54, you may want to use 4.48, but to do that, you need to select a generator $g$ for $\mathbb{Z}_m$ and translate the notation $g^k$ to additive notation. As we saw today, $1$ is always a generator for $\mathbb{Z}_m$, and additively, $1^k$ should be written $k\cdot 1 = k$. Also, if you want another reference for modular arithmetic, you could see if my number theory notes (about congruences) help at all: webpages.csus.edu/wiscons/teaching/math102_s18/Section4.pdf.
Please read Section 4.2 even though I'm not asking you to do any problems for in the section. It ties together (and generalizes) many of our observations from before.
Right before the last problem, the book introduces "cycle notation". For example, one of the permutations is written as $\sigma = (1,3)(2,5,4)$. How do you read this? You should read left to right, and cycle around in each set of parentheses. So, this means that $\sigma(1) = 3$ and $\sigma(3) = 1$. Also, $\sigma(2) = 5$, $\sigma(5) = 4$, and $\sigma(4) = 2$. Do your best with this, and we'll talk more about it on Tuesday.
Homework 18 (Due Thursday 4/4)
- Read: Continue with 4.1.
- Turn in: 4.36, 4.37, 4.38, 4.43, 4.44, 4.47, 4.48, 4.51
- To try but not turn in: 4.42
As you start working with $\mathbb{Z}_n$ and $U_n$, remember that the operation is addition for $\mathbb{Z}_n$ but multiplication for $U_n$. Also, one small trick for working modulo $n$ is that you can always add or subtract $n$ without changing the object. For example, $5,7\in U_{12}$, so $5*7 = 35 = 35 - 12 - 12 = 11$ (mod $12$). Thus, in $U_{12}$, $5*7 = 11$. Similarly, in $\mathbb{Z}_{12}$, $5+7 = 12 = 12-12 = 0$ (mod $12$), so $5+7 = 0$ in $\mathbb{Z}_{12}$. Feel free to look at other resources (e.g. https://en.wikipedia.org/wiki/Modular_arithmetic) to fill in background about modular arithmetic if needed.
For 4.44, consider using 4.42. Please read Theorem 4.42 carefully—it's very important. Try to prove it too! (4.42 is kind of hard. You can write $G = \langle g \rangle$, and then your first task it to try to guess a generator for $H$. Spoiler alert!! ...for a generator of $H$, try choosing $a = g^k$ where $k$ is the smallest positive integer such that $g^k \in H$.)
For 4.47, 4.48, and 4.51, you will likely want to use 4.45 and 4.46.
Homework 17 (Due Tuesday 4/2)
- Read: Continue with 4.1.
- Turn in: 4.20, 4.21, 4.22, 4.24, 4.25, 4.28, 4.29
- To try but not turn in: 4.19, 4.27
When thinking about 4.19, make sure to read the hint in the footnote. For 4.20, you should use 4.19, and your proof might only be one sentence.
Note that 4.24 is an "if and only if" statement, so there are two things to show. For the "backward" direction, you will assume that $n$ divides $i-j$; what does this imply about $g^{i-j}$? For the "forward" direction, you assume $g^i = g^j$ and want to prove that $n$ divides $i-j$. One strategy for proving that $n$ divides $i-j$ is to use the division algorithm to write $i-j = qn +r$ where $0\le r < n $ (note that $r$ represents the remainder when dividing $i-j$ by $n$); then prove that $r = 0$. For 4.25, you should use 4.24 (even if you don't complete the proof of 4.24).
For 4.29 you will want to construct an isomorphism between $G$ and $\mathbb{Z}$. I recommend defining it from $\mathbb{Z}$ to $G$ like this: $\phi:\mathbb{Z} \rightarrow G$. You know $G$ is cyclic, so $G = \langle g \rangle = \{g^m \mid m \in \mathbb{Z}\}$. To define $\phi$, you need to decide how to finish this equality: $\phi(m) = g^{?}$. Once you've done this, you need to verify that the $\phi$ you defined is one-to-one, onto, and a homomorphism. You will need 4.28; do you see why?
And here's a challenge problem, for fun. In 4.20, you proved that if $G$ is finite, then $\forall g\in G$, $\exists n\in \mathbb{N}$ such that $g^n = e$. What happens if you switch the order of the quantifiers. Try to prove this: if $G$ is finite, then $\exists n\in \mathbb{N}$ such that $\forall g\in G$, $g^n = e$. Do you see the difference?
Homework 16 (Due Thursday 3/28)
- Read: Continue with 4.1.
- Turn in: 4.3(b,d,f,g,k,l), 4.5, 4.8, 4.10, 4.12(b,d,f,g,k,l), 4.13, 4.14, 4.18
- To try but not turn in: 4.17
On 4.3, if a group is not cyclic, you can just say so without proof. For 4.5, you may want to begin with "Since $G$ is cyclic, $G = \langle g \rangle$ for some $g\in G$." This means that every $x\in G$ can be written as $x=g^m$ for some $m\in \mathbb{Z}$, which you can use to prove that $G$ is abelian. On 4.10, the hypothesis is that $G$ has no proper nontrivial subgroups. This means that if you create a subgroup of $G$, it must be either $\{e\}$ or $G$.
When thinking about 4.17, make sure to read the hint in the footnote. Remember that $\langle g\rangle = \{\ldots,g^{-2},g^{-1},e,g,g^2,\ldots\}$, so if $\langle g\rangle$ is finite, there must be repetitions in the list. For the reverse direction, assume that $g^n = e$, and try to use this to prove that for any $m\in \mathbb{Z}$, $g^m$ is equal to one of $e,g,g^2,\ldots,g^{n-1}$. This would show that $\langle g\rangle \subseteq \{e,g,g^2,\ldots,g^{n-1}\}$, implying that $\langle g\rangle$ is finite. On 4.18, you should use 4.17.
Homework 15 (Due Tuesday 3/26)
- Read: Finish 3.3 and start 4.1.
- Turn in: 3.47, 3.54, 3.58, 3.59, 3.61, 3.63, 4.1, 4.2
- To try but not turn in: 3.53, 3.55, 3.60, 3.62
For 3.47, your answers should look like lists of isomorphic groups with a short justification like "$D_4 \cong \operatorname{Spin}_{1\times 2}$ as shown by the matching we found in 3.35." As you explore some of the groups that we hadn't thought of before, here are some things to keep in mind: (1) isomorphisms are bijections so groups of different sizes cannot be isomorphic, and (2) isomorphic groups must share the same group-theoretic properties so if one group has 6 elements with the property that $g^2=e$ and another group only has 2 elements with that property, then they can't be isomorphic.
For 3.53, remember that since $\phi:G_1 \rightarrow G_2$ is a bijection, $\phi^{-1}: G_2\rightarrow G_1$ is a function and is also a bijection. You do not need to prove this. Also, remember the relationship between a function and its inverse: $\phi^{-1}(\phi(x)) = x$ and $\phi(\phi^{-1}(y)) = y$. To prove that $\phi^{-1}: G_2\rightarrow G_1$ has the homomorphic property, you should start by considering $\phi^{-1}(y_1+y_2)$ for $y_1,y_2 \in G_2$. You will need to find a way to rewrite $y_1$ and $y_2$ to move forward. For 3.54, you can use (without proof) that the composition of bijections is a bijection.
For 3.60, you should assume that $G_1$ is cyclic, so $G_1 = \langle a \rangle$ for some $a\in G_1$. This means that for all $g\in G_1$ there exists a $k\in \mathbb{Z}$ such that $g = a^k$. Now, to show that $G_2$ is cyclic, you need to find a $b\in G_2$ such that for all $h\in G_2$ there exists a $m\in \mathbb{Z}$ such that $h = b^k$. Thus, your first task is to try to guess what $b$ might be. For both 3.60 and 3.61, you will need to make use of the fact that $\phi$ is onto; this implies that every element $y \in G_2$ can be written as $y = \phi(x)$ for some $x\in G_1$.
Homework 14 (Due Thursday $\approx\pi$)
- Read: Continue with 3.3.
- Turn in: 3.48, 3.49, 3.50, 3.52, 3.56, 3.57
Feel free to think about 3.47, but we will save it for next time (after you get the last homework back). We'll also save 3.53–3.55.
For 3.47 and 3.48, you are given a function and need to check three things: (1) does it satisfy the homomorphic property in Definition 3.46, (2) is it one-to-one, and (3) is it onto. If any one of them fails, it is not an isomorphism. On 3.50, you need to first come up with a function from $\mathbb{Z}$ to $2\mathbb{Z}$, and then verify the three things listed in the previous sentence.
There are multiple ways to approach 3.51 and 3.52. If you want a hint on these, read on; if not, don't. For 3.51, you could consider the fact that $\phi(e_1) = \phi(e_1*e_1)$, and for 3.52, you could meditate on the equation $\phi(e_1) = \phi(g*g^{-1})$.
Homework 13 (Due Tuesday 3/12)
- Read: Start of 3.3.
- Turn in: 3.33, 3.35, 3.36, 3.37, 3.38, 3.39, 3.40, 3.41, 3.42, 3.43
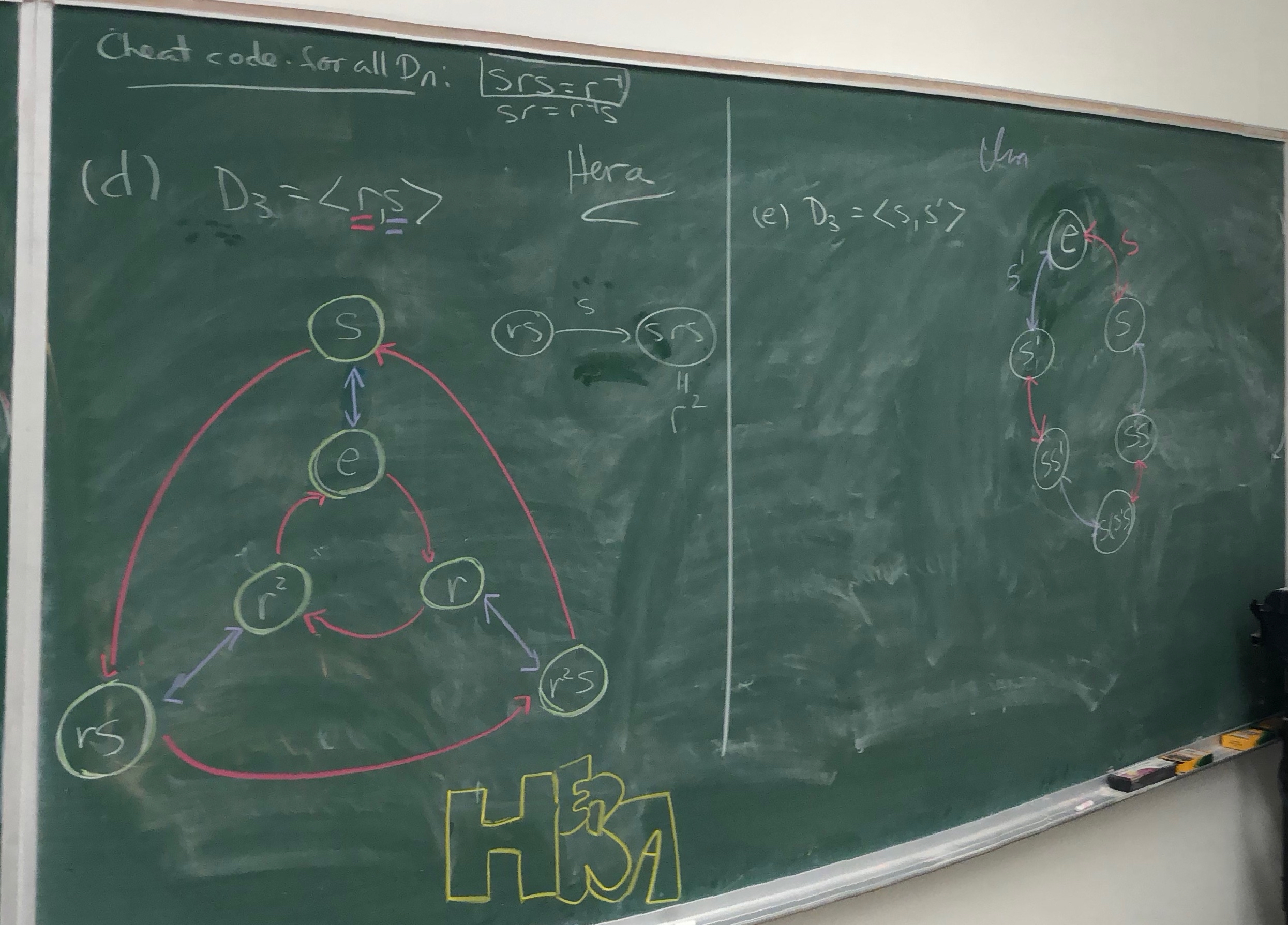
On 3.33, you'll need to find a generating set for $S_3$ different than $\{s_1,s_2\}$ in order to match it with the diagram for $D_3 = \langle r,s\rangle$. You'll want two elements in $S_3$ with similar behavior as $r$ and $s$ in $D_3$. Keep in mind that $s^2=e$ (much like $s_1$ and $s_2$ in $S_3$) but $r^3=e$.
As usual, you can use 3.34 even though you are not asked to prove it. For 3.35–3.38, the paragraph right before 3.35 is really helpful! And finally, 3.42 and 3.43 are NOT asking for rigorous proofs, but rather just a brief explanation.
Homework 12 (Due Tuesday 3/05)
- Read: Continue with 3.2, and start 3.3.
- To look over but not turn in: 3.26, 3.30, 3.31, 3.33, 3.34, 3.35, 3.36
- Turn in: 3.24, 3.27, 3.32
On 3.24, you need to prove two things: (1) that $H\cap K$ is a subgroup, and (2) that it is the largest subgroup contained in both $H$ and $K$. To prove the (2), try starting like this: "Assume that $A$ is a subgroup of $G$ such that $A$ is contained in both $H$ and $K$. We will show that $A$ is contained in $H\cap K$. Observe that..."
Please try to look over all of the problems listed above, but the number of problems to turn in is considerably smaller this time so that you can focus on synthesizing the material and preparing for the exam.
Homework 11 (Due Thursday 2/28)
- Read: Continue with 3.1, and start 3.2.
- Turn in: 3.21, 3.22, 3.25, 3.28, 3.29
When reading about the center of a group, here's some extra terminology that may help. If $g,h$ are elements of a group for which $gh = hg$, we say that $g$ commutes with $h$ (and $h$ commutes with $g$). Thus, $z$ is in $Z(G)$ iff $z$ commutes with every element of $G$.
As before, you will probably want to use 3.6 to prove 3.21. Before working on 3.22, try to solve the following problem: the elements of $Z(G)$ are those that commute with every element of $G$, so if $G$ happens to be abelian, then it must be that $Z(G) = $ (fill in the blank) . If you can answer this question, you will be able to quickly answer over half of 3.22. Try hard (as usual) on 3.22, but if you get stuck on some of the parts, don't worry too much.
Homework 10 (Due Tuesday 2/26)
- Read: Continue with 3.1.
- Turn in: 3.7, 3.12, 3.13, 3.14, 3.15, 3.16(a,b,c), 3.18, 3.19, 3.20
Note that there are a few theorems that I am not asking you to prove, but you are still allowed to use them. In particular, Theorem 3.6 is usually the preferred way to determine if a nonempty subset is a subgroup or not.
Even if 3.7 seems obvious, please write the proof out carefully (though it will likely be very short). In 3.13, you can use the Cayley diagram for $D_4$ to build intuition, but you should use Theorem 3.6 to carefully prove whether or not each set is a subgroup. Also, in 3.16, 3.17, please use Theorem 3.6 to prove or disprove if the set is a subgroup.
Homework 9 (Due Thursday 2/21)
- Read: Continue with 2.6 and start 3.1.
- Turn in: 2.70, 2.71(a,c), 3.2, 3.3, 3.5
For 2.70, instead of coloring the edges according to the generators, you can just label the edges with the generator. For example, when making the diagram for $D_3$ with generating set $\{r,s\}$, you can just label the edges corresponding to $r$ with an $r$ and those for $s$ with an $s$ instead of making $r$ edges red and $s$ edges blue.
You know that a Cayley diagram should have one vertex for every element of your group, so in 2.70, you will have a hard time drawing the complete Cayley diagram for the group $(\mathbb{Z},+)$, which is why the directions ask you to "draw a portion of the diagram". For parts (a) and (b), please draw the portion including all integers between $-2$ and $2$, and for part (c), please draw the portion including all integers between $-6$ and $6$.
Homework 8 (Due Tuesday 2/19)
- Read: Finish 2.5 and start 2.6. There is a lot to read in 2.6— try to go slowly and carefully.
- Turn in: 2.60, 2.61, 2.62, 2.63, 2.64, 2.66, 2.67, 2.69
For 2.63, you should be able to create a proof without making a table. Try something like this: "Suppose that the element $b$ appears twice in the row corresponding to $g$." What does this mean? There should be two different columns (which correspond to two different group elements $h_1$ and $h_2$) such that...
When you read 2.69, note that the diagram it refers to is on the next page.
Homework 7 (Due Thursday 2/♥)
- Read: Finish 2.4 and start 2.5.
- Turn in: 2.56, 2.57, 2.58, 2.59
Homework 6 (Due Tuesday 2/12)
- Read: Finish 2.3 and start 2.4.
- Turn in: 2.44, 2.45, 2.48, 2.50, 2.53, 2.54, 2.55
Remember that many of these will have short proofs, especially if you make use of previous theorems (which you should!). For 2.44, try going back to the definition of inverse: $(g^{-1})^{-1}$ is the inverse of $g^{-1}$, so what property should $(g^{-1})^{-1}$ have? Also note that I'm not asking you to prove 2.47, but you can certainly use it for later problems.
When you read about words and generating sets, it is extremely important to note that when forming words from elements of a set $S$ you can use elements of $S$ and also inverses of elements of $S$. When proving 2.50, there are several things to consider. Make sure to start by showing that $\langle S\rangle$ is closed under $*$. This amounts to explaining why if $w_1$ and $w_2$ are words in $S$, then $w_1*w_2$ is also a word in $S$. Then try to use information about $G$ to claim that $*$ is associative on $S$. (You should not have to work too hard for associativity.) For identity and inverses, try to explicitly show that $e$ is a word in $S$, and that given any word $w=s_1\cdots s_n$ in $S$, that $w^{-1}$ is again a word in $S$.
Homework 5 (Due Thursday 2/07)
- Read: Continue 2.3
- Turn in: 2.38, 2.39, 2.41, 2.42, 2.43
Many of these theorems can be proved multiplying both sides of an equation you know to be true by the same thing. However, since the operation may not be commutative, if you multiply one side of the equation by something on the left, then you need to do the same on the other side too. For example, if you know that $gx = gy$, then for any $h\in G$ it is also true that $h(gx) = h(gy)$; however, $h(gx) = (gy)h$ may not be true. (Do you see the difference?) To solve 2.39, choose something clever for $h$ so that you arrive at $x=y$.
To prove 2.41 you'll want to do something similar to 2.37. Try starting this way... "Let $G$ be a group, and let $g\in G$. Assume that there exists $g',g''\in G$ such that $gg' = g'g = e$ and $gg'' = g''g = e$. We will show that $g'=g''$."
Homework 4 (Due Tuesday 2/05)
- Read: Rest of 2.2, beginning of 2.3, and skim through Appendix C: Definitions in Mathematics
- Turn in: 2.26, 2.27, 2.28, 2.31, 2.32, 2.34, 2.35, 2.36, 2.37
Although I'm not asking you to prove 2.29, please read it over, and know that you can use it in the future. (That theorem is something proved in our Math 108 course.) For 2.35, make sure to explain why each of the axioms is true. You can refer to what we proved in earlier problems (without reproving them) AND you can also use 2.29, but please make it clear when you are using them.
And my final comment is about 2.37. This is our first theorem to prove—yay! Here is a hint on how to start. "Let $G$ be a group. Assume that $e_1$ and $e_2$ are identity elements. We will show that $e_1=e_2$." What I'm saying is that a good way to show that there is only one element with a certain property is to assume you have two and then show that they are the same. To continue the proof, you will need to use that axiom 2 is valid for both $e_1$ and $e_2$ and then manipulate things to arrive at $e_1=e_2$.
Homework 3 (Due Thursday 1/31)
- Read: The beginning of 2.2 and Appendix B: Fancy Mathematical Terms
- Turn in: 2.17, 2.18, 2.19, 2.20, 2.21, 2.22, 2.23, 2.24
Feel free to look up background terms, like the power set of a set, if you're unclear on their definitions.
Homework 2 (Due Tuesday 1/29)
- Read: The rest of 2.1 and Appendix A: Elements of Style for Proofs
- Turn in:
- Short paragraph addressing one item from your reading from Appendix A that you had not thought about before and/or did not think was important. (This is based off of the Appendix A reading.)
- Solutions to (or your best efforts on): Problems 2.7, 2.8, 2.9, 2.10, 2.11, 2.12, 2.13, 2.14
Homework 1 (Due Thursday 1/24)
- Read: Sections 1.1, 1.2, 1.3, and beginning of 2.1 (see our book)
- Turn in:
- Short paragraph about one aspect of an IBL approach that you view as positive and one concern that you have.
(This is based off of the 1.2 reading.) - Solutions to (or your best efforts on): Problems 2.1, 2.2, 2.3, 2.4, 2.5 (see Chapter 2 of our course book)
- Short paragraph about one aspect of an IBL approach that you view as positive and one concern that you have.
Writing Assignments
Other Handouts
Course Log
| Week 15 |
|---|
|
[5.09.19] - Thursday
Last day—boom! Thanks to EVERYONE!!! ...with extra thanks to the presenters: AF, NC, JS, HF . |
| What we covered: 7.3, 7.7, 7.13, 7.15(a,b), 7.21, 7.23 |
|
|
|
[5.07.19] - Tuesday
Covered a lot today: more with direct products, more with quotients, and kernels and images of homomophisms. Many thanks to the presenters: MP, SB, EO, IM, KP, YR, IS, BT. |
| What we covered: 6.16, 6.19, 6.32(d), 6.38, 6.39, 7.5(c), 7.9 + 7.10, 7.11 |
| Week 14 |
|
[4.30.19] - Thursday
Great class today! We covered material about Lagrange's Theorem, normal subgroups, direct products, and quotients, with lots of excellent presentations. Many thanks to MKH, BT, AA, AE, HF, JS, DB, MP. (Picture of our victories below, but the panoramic option did some strange things to you all...) |
| What we covered: 5.21, 5.33, 6.9 (just part a for now), 6.11, 6.12, 6.13 6.28, 6.32(a,b,c), 6.36 |
|
|
|
[4.30.19] - Tuesday
I accidentally swapped which problems were to be turned in and which were to be "tried but not turned in." We made the best of it and worked on many of the problems together in small groups. It turned out to be quite a fun and productive class—thanks all! |
| Week 13 |
|
[4.25.19] - Thursday
Exam 2 |
|
[4.23.19] - Tuesday
Another mini-lecture, this time about applications of Lagrange's Theorem, normal subgroups, and a quick look at quotient groups. As we went, we ended up covering 5.19, 5.20, 5.21, 5.22, 5.24, 5.30, 5.32. |
| What we covered: applications of Lagrange and normal subgroup mini-lecture |
| Week 12 |
|
[4.18.19] - Thursday
For better or worse, I took up the entire time with a lecture on cosets. Along the way we covered 5.11 (and kind of 5.10), 5.12 (and 5.13), much of 5.14, and 5.16. |
| What we covered: Coset mini lecture |
|
[4.16.19] - Tuesday
Covered lots of ground. Started with a bit about the alternating groups today, and then moved on to cosets. Great day! Yay presenters: IS, GH, MP, NC, MDS, IM + JS + DB. |
| What we covered: 4.97 + 4.101 (me), 4.102, 4.104, 4.108, 4.109, 5.2, 5.4 |
|
|
| Week 11 |
|
[4.11.19] - Thursday
More discussion about cycle notation today, finishing with more-or-less a proof that $S_n$ is generated by its transposition. Our amazing presenters today were: YR, AE, MKH, IL, DB, GH, BT. |
| What we covered: 4.73, 4.74, 4.76, 4.78, 4.81 + 4.82, 4.87, 4.88 |
|
[4.09.19] - Tuesday
Wrapped up cyclic groups today and got started on a deeper analysis of symmetric groups. We ended with a short discussion of cycle notation. Thanks all around, especially to the presenters: HF, EY + JS, IS, KP, AE, SB. |
| What we covered: 4.49, 4.53, 4.64 + 4.70, 4.66, 4.68, 4.72 |
| Week 10 |
|
[4.04.19] - Thursday
Excellent day! We covered lots of ground, had good discussion, and covered the boards with beautiful math! Thanks to the presenters: HF, NC, MKH, JN, YR, DB, EY, HR!! |
| What we covered: 4.36, 4.37, 4.38, 4.43, 4.44, 4.47, 4.48, 4.51, 4.42 |
|
|
|
[4.02.19] - Tuesday
More about cyclic groups and orders of elements today. Many tahnks to the presenters EO, NB, AF, IM, MDS, BT, and HF. Thanks all! |
| What we covered: 4.17, 4.20, 4.21, 4.22, 4.24, 4.25, 4.28, 4.29 |
| Week 9 |
|
[3.28.19] - Thursday
Started with me talking a bit more about isomorphisms by presenting proofs for Theorems 3.60 and 3.62. We then transitioned to the homework by discussing (some of) 4.3 and 4.12 together. We finished with presentions by AF, SB, IL, JB, and BT. Thanks all! |
| What we covered: 4.3, 4.5, 4.8, 4.10, 4.12, 4.13, 4.14 |
|
[3.26.19] - Tuesday
Began by discussing 3.47 as a class before moving into presentations on the rest—many thanks to KP, MDS, IS, GH, JS, EO, JB! |
| What we covered: 3.47, 3.54, 3.58, 3.59, 3.61, 3.63, 4.1, 4.2 |
| Week 8 |
|
[$\approx\pi$.19] - Thursday
Started off with a mini-lecture about what it means for a function to be one-to-one (injective), onto (surjective), and bijective. We then got lots of great work on the board, but unfortunately we had to rush through the discussion at end. Hopefully you all got some good pictures. Also, we didn't get through 3.56 or 3.57, so we'll do them next time. Thanks for all of the hard work! And many thanks to the presenters too: NB, AA, NC, ??, IL, HR, IM |
| What we covered: 3.48, 3.49(a,b,c), 3.50, 3.51, 3.52 |
|
[03.12.19] - Tuesday
Talked a lot about matchings today, which is building intuition for the next big concept: isomorphism. Fantastic (and super colorful) presentations today! Thanks to everyone! |
| What we covered: 3.33, 3.35, 3.36, 3.37, 3.39, 3.40, 3.41 |
| Week 7 |
|
[03.05.19] - Thursday
Exam day! You all have worked super hard—I hope it goes really well! |
|
[03.05.19] - Tuesday
NC led off by showing that the intersection of two subgroups is a subgroup, and then DB and AA presented the subgroup lattices for $R_5$ and $Q_8$. After that, I discussed some generalities about subgroup lattices before leading us through the construction of the subgroup lattice for $D_4$. |
| What we covered: 3.24, 3.27, 3.32, 3.10, 3.26, 3.31 |
| Week 6 |
|
[02.28.19] - Thursday
Started off by talking about a couple of problems from last time: 3.15, 3.16 (both of which are on the upcoming writing assignment. Next, IL, KP, and HR presented some theorems and problems about the center of a group. We wrapped up by looking at the work of JN, IS, and MDS about subgroups and subgroup lattices. Thanks to everyone. |
| What we covered: 3.21, 3.22 (a,b,d,e), 3.25, 3.28, 3.29. |
|
[02.26.19] - Tuesday
Covered a lot of ground, but sadly ran out of time at the end. Thanks for your patience as we quickly ran through 3.15 and 3.19 at the end. We never made it to 3.16, but we will next time (and there is a picture below). As always, thanks to the presenters: AE, SB, EO, DB, YR, MP. |
| What we covered: 3.7, 3.13, 3.14, 3.15, 3.16 (on the board, but will talk through it next time), 3.19. |
|
|
| Week 5 |
|
[02.21.19] - Thursday
Tons of beautiful Cayley Diagrams today as well as some initial talk of subgroups. Thanks to you all, with special thanks to the presenters: GH, AA, JS, HF, IM BT, HR, NB. |
| What we covered: 2.70 (all parts!), 2.71, and some discussion around 3.2, 3.3, 3.5. |
|
|
|
[02.19.19] - Tuesday
Lots of group tables and Cayley Diagrams today. Great presentations with lots of colorful pictures! Thanks to all, especially the presenters: KP, IL, MKH, YR, JB, AF, EY, EO. |
| What we covered: 2.60, 2.61, 2.62, 2.63, 2.64, 2.66, 2.67, 2.69 |
|
|
| Week 4 |
|
[02.♥.19] - Thursday
More discussion of generating sets today, as well as group tables. We learned a lot about $D_4$! ...as well as $S_3$ and $(\mathbb{Z},+)$. Many thanks to the presenters: JN, MKH, SB, BT. And also a huge thanks to KP for the chocolate. Happy Valentine's Day! |
| What we covered: 2.56, 2.57, 2.58, 2.59 |
|
[02.12.19] - Tuesday
Covered a lot of ground today, including a mini-lecture from me about generating sets. Unfortunately it got a bit rushed at the end—sorry! A picture of the last one we did (Theorem 2.50) is included below. Many thanks to the presenters: AE, GH, JS, NB, IS, DB. |
| What we covered: 2.44, 2.45, 2.50, 2.53, 2.54, 2.55 |
|
|
| Week 3 |
|
[02.07.19] - Thursday
We had a big round of proofs today, and they went great!! Many thanks to EO, AA, AF, JS, EY, and KP! (And sorry for the terse reports this week...) |
| What we covered: 2.37, 2.38, 2.39, 2.41, 2.42, 2.43 |
|
|
|
[02.05.19] - Tuesday
Lots of great presentations and discussions today. Thanks to everyone, especially our presenters: IL, MP, NC, MDS, HR, and IM! |
| What we covered: 2.26, 2.27, 2.28, 2.31, 2.32, 2.35 |
|
|
| Week 2 |
|
[01.31.19] - Thursday
We covered a lot of ground today, focusing mostly on examples and nonexamples of binary operations. SB lead it off with addition and multiplication for matrices; then YR discussed union and intersection for the power set of a set. Next was EY presenting that $\operatorname{min}$ is a binary operation on $[0,1]$. We then started to explore symmetries of shapes. BN discussed rotaions of the square, AE talked about all symmetries of an equilateral triangle, and NC presented on all symmetries of a square. There were beautiful pictures all over the board! Next, BT explored rearrangements of three coins, and finally HF showed us that composition is NOT a binary operation on the set of spins for Spinpossible. In the final minutes, we returned to 2.13 with MDS showing us how to create the toggle $s_{33}$ just using the specific spins in the set $T$. THanks everyone!! |
| What we covered: 2.17, 2.18, 2.19, 2.20, 2.21, 2.22, 2.23, 2.24, 2.13 |
|
|
|
[01.29.19] - Tuesday
IS led it off by talking us through an algorithm showing that every scrambled board can be solved by some sequence of spins. Next, NB presented how to count the size of $\operatorname{Spin}_{3\times 3}$. He came up with $2^9\cdot 9!$ (which is correct!), but we discussed that the proof needs to make sure to account for all net actions, not just the spins. HR gave a very detailed proof of the fact that the inverse of a sequence of spins is the inverse of the spins (which are themselves) in the reverse order. Next, DB shoed us some spins that do not commute and also conjectured that two spins will commute whenever they move disjoint sets of positions. Then JN discussed why the set $T$ should generate $\operatorname{Spin}_{3\times 3}$, and then we used that to conclude that the set of spins is not a minimal generating set for $\operatorname{Spin}_{3\times 3}$ (because $T$ is a smaller collection of spins that still generates $\operatorname{Spin}_{3\times 3}$). We ended with MKH showing that the identity can always be created by composing a spin with itself. Another great day—thanks! |
| What we covered: 2.7, 2.8, 2.9, 2.10, 2.11, 2.12 |
|
|
| Week 1 |
|
[01.24.19] - Thursday
Started with IM talking us through how to count the number scrambled boards (with the audience chiming in on some other approaches). The idea was to first choose which tile would be in each of the nine positions (giving $9!$ possibilities) and then account for the fact that each of the 9 tiles could be right-side-up or up-side-down (giving another $2^9$ possibilities). Thus, there were $9!2^9$ possibilities in all. Then AF and JB showed us two different ways to count the number of spins; there were 36. Next, MP showed us a different way to unscramble the board from the notes, which most of us agreed took some serious time to find. After that, YK explained that $s_{23}s_{21}s_{23}$ and $s_{12}s_{23}s_{12}$ have the same net action (which was to swap the tiles in the first and third positions); thus, as functions, $s_{23}s_{21}s_{23}=s_{12}s_{23}s_{12}$. Finally, HF showed us that $(s_{23}s_{12})^2 = s_{12}s_{23}$, which generated discussion on whether $s_{12}s_{23}$ means to apply $s_{12}$ or $s_{23}$ first. (For our book, we work right-to-left: $s_{12}s_{23}$ means to first apply $s_{23}$ and then $s_{12}$. However, other books work left-to-right.) Afterwards, we also deduced that $(s_{12}s_{23})^2 = s_{23}s_{12}$. There were also lots of comments from the audience throughout the presentations. Awesome day—thanks to everyone! |
|
What we covered: 2.1–2.5
|
|
[01.22.19] - Tuesday - First day!
Great to meet you all! |
|
What we covered: The community Agreement, some generalities, and an introduction to Spinpossible: www.kongregate.com/games/spinpossible
|