الجبر

الجبر (al-jabr) roughly means to "restore" or "complete" and is from the title of the book Al-kitāb al-mukhtaṣar fī ḥisāb al-ğabr wa’l-muqābala by Muḥammad ibn Mūsā al-Khwārizmī (circa 820 CE)

The Book

We will use the (in-progress) open-source book Insolvability of the Quintic, by me. The book is being developed throughout the semester, so you will frequently need to download the latest version. I'm sorry for any inconvenience!

To keep us on the same page, I will periodically release stable versions of each chapter as we go.

• Title Page and Front Matter [updated 08.19.19]
• Chapter 1: Introduction [updated 08.19.19]
• Chapter 2: Solving polynomial equations and the main question [updated 08.28.19]
  • Please use the old version for Homework 1: Chapter 2 — 08.20.19 version
• Chapter 3: Fields [updated 09.17.19]
• Chapter 4: Solvability by Radicals [updated 09.19.19]
• Chapter 5: Rings [updated 10.25.19]
• Chapter 6: Algebraic extension fields [updated 11.19.19]
• Chapter 7: Galois theory [updated 12.03.19]
• Chapter 8: End game [updated 12.03.19]
• Appendix A: Hints [updated 12.03.19]

The most current, complete version of the notes (which is often unstable!), can be found on GitHub here: Insolvability of the Quintic

Daily Homework

Reading/working Homework (Due Thursday 12/05)

• Read/work: Read: Chapter 8. Work: take a look at the final project. Try to prove one of Theorems 2.3 or 3.3 (or both).
• Turn in: nothing, but please work on the items listed above. I'll be discussing the end of Chapter 7 as well as Chapter 8 in class on Thursday.

Homework 25 (Due Tuesday 12/03)

• Read: Chapter 7: up through 7.38
• Turn in: 7.20, 7.21, 7.22, 7.23, 7.24, 7.28, 7.29, 7.31, 7.32

  Please, please, please read all the way to Fact 7.38; it was a huge goal of the course!

Homework 24 (Due Tuesday 11/26)

• Read: Chapter 7: up through 7.17
• Turn in: 7.2, 7.3, 7.4, 7.7, 7.10, 7.11, 7.17, 7.18

Homework 23 (Due Thursday 11/21)

• Read: Continue with Chapter 6: Problem 6.66 through the end of the chapter
• Turn in: 6.72, 6.74, 6.76, 6.77, 6.79, 6.80

  Make sure to re-download Chapter 6. I fixed several typos in Example 6.73 and Problem 6.77!

  Please make sure to read 6.81. I'll present that one.

Reading Homework (Due Tuesday 11/19)

• Read: Continue with Chapter 6: Problem 6.66 through Problem 6.74
• Turn in: nothing, just work on the midterm

  Make sure to get the newest copies of the notes. The last page of the Chapter 6 notes from before has changed!

Homework 22 (Due Thursday 11/14)

• Read: Continue Chapter 6, up through 6.65
• Turn in: 6.50, 6.60, 6.61, 6.62, 6.63, 6.64, 6.65

Homework 21 (Due Tuesday 11/12)

• Read: Continue Chapter 6, up through 6.55
• Turn in: 6.42, 6.43, 6.45, 6.47, 6.48, 6.49, 6.51, 6.55

Homework 20 (Due Tuesday 11/07)

• Read: Continue Chapter 6, up through 6.41
• Turn in: 6.28, 6.29, 6.30, 6.31, 6.39, 6.41 (we'll also present 6.22)

Homework 19 (Due Thursday 11/05)

• Read: Continue Chapter 6, up through 6.27
• Turn in: 6.18, 6.20, 6.21, 6.22, 6.23, 6.24, 6.26, 6.27

Homework 18 (Due Thursday )

• Read: Continue Chapter 6, up through 6.17
• Turn in: 6.9, 6.10, 6.11, 6.12, 6.14, 6.16, 6.17 (we'll also present 6.5)

  When you get to 6.16, you've already done most of the work: 6.8 and 6.14 should be helpful.

Homework 17 (Due Tuesday 10/29)

• Read: Finish Chapter 5 and start Chapter 6, up through 6.6
• Turn in: 5.120, 5.122, 5.123, 5.125, 6.2, 6.3, 6.4, 6.5

  As usual, you can use all previous results, even if we haven't proved them. In particular, you can use both 5.121 and 5.122 to prove 5.123 even though you are not asked to prove 5.121.

Homework 16 (Due Tuesday 10/24)

• Read: Continue with Chapter 5, up through 5.118
• Turn in: 5.107, 5.108, 5.110, 5.112, 5.114, 5.115, 5.117(1), 5.118

Homework 15 (Due Tuesday 10/22)

• Read: Continue with Chapter 5, up through 5.86
• Turn in: 5.87, 5.90, 5.96, 5.98, 5.99, 5.100, 5.104, 5.105

Homework 14 (Due Thursday 10/17)

• Read: Continue with Chapter 5, up through 5.86
• Turn in: 5.78, 5.79, 5.80, 5.82, 5.83, 5.85, 5.86

  Make sure to get the newest copies of the notes. Problem 5.80 has changed!

Homework 13 (Due Tuesday 10/15)

• Read: Continue with Chapter 5, up through 5.62
• Turn in: 5.61, 5.64, 5.65, 5.66, 5.68, 5.71, 5.72, 5.77

Homework 12 (Due Thursday 10/10)

• Read: Continue with Chapter 5, up through 5.62
• Turn in: 5.46, 5.52, 5.53, 5.55, 5.58, 5.59, 5.62

  We'll be skipping over a few results (like 5.51, 5.60, 5.61), but remember that you can always use them for future problems (even if we don't prove them now).

Reading Homework (Due Tuesday 10/08)

• Read: Continue with Chapter 5: Corollary 5.37 through Definition 5.50
• Turn in: nothing, just work on the midterm

Homework 11 (Due Thursday 10/03)

• Read: Continue with Chapter 5
• Turn in: 5.24, 5.25, 5.27, 5.28, 5.30, 5.32, 5.35, 5.36

Homework 10 (Due Tuesday 10/01)

• Read: Continue with Chapter 5
• Turn in: 5.8, 5.12, 5.13, 5.15, 5.17, 5.18, 5.19, 5.20

Homework 9 (Due Thursday 9/26)

• Read: Finish Chapter 4, and start Chapter 5
• Turn in: 4.12, 4.13, 4.14, 5.2, 5.3, 5.4

Homework 8 (Due Tuesday 9/24)

• Read: Start Chapter 4
• Turn in: 4.3, 4.4, 4.6, 4.8, 4.9, 4.10, 4.11

Homework 7 (Due Thursday 9/19)

• Read: Continue with Chapter 3: Section 3.3.6 through the end of Chapter 3
• Turn in: 3.66 (redo), 3.67, 3.68, 3.69, 3.70, 3.71, 3.72, 3.73

  I'm asking you to redo 3.66 if you want. We'll do the presentation for it on Thursday. We'll also revisit 3.64 and 3.65.

  You can do Problem 3.67 without actually finding a nice form for the elements of $\mathbb{Q}(\alpha)$, which is quite hard at this point. You just need to work with the definition of $\mathbb{Q}(\alpha)$ and remember that we saw (in Problem 3.57) that $\{a+b\alpha\mid a,b\in\mathbb{Q}\}$ is not a field.

  For Problem 3.69, you should consider using Theorem 3.68. Remember to prove the LHS is contained in the RHS and vice versa.

Homework 6 (Due Tuesday 9/17)

• Read: Continue with Chapter 3: Section 3.3.4 through the middle of 3.3.6
• Turn in: 3.51, 3.53, 3.56, 3.57, 3.58, 3.62, 3.64, 3.65, 3.66

  In Theorem 3.53, you can state as fact (without proof) that $\mathbb{Z}_n$ has associative and commutative addition and multiplication. You can also state as fact that the distributivity laws holds.

  I am not asking you to prove Theorem 3.55, but please feel free to use it for later problems.

Homework 5 (Due Thursday 9/12)

• Read: Continue with Chapter 3: Section 3.3.1 through the end of 3.3.3
• Turn in: 3.43, 3.44, 3.45, 3.47, 3.48, 3.50 (1,2,3,4)

  Just to clarify, you don't need to do part (5) of 3.50.

Homework 4 (Due Tuesday 9/10)

• Read: Continue with Chapter 3: Section 3.2 and the beginning of 3.3
• Turn in: 3.25, 3.33, 3.34, 3.36, 3.37, 3.38, 3.39, 3.40

  In problems 3.36 and 3.37, you are asked to prove certain subsets $G$ and $S$ of $\mathbb{H}$ are groups. The first thing to address is why the operation is actually an operation $G$ and $S$; that is, you need to explain why $G$ and $S$ are closed under the operation. Another thing you need to address is why the operation is associative, but in both cases the operation is already know to be associate with respect to the larger set $\mathbb{H}$. Thus, you can use this observation to simply state that the operation is associative when restricted to the smaller sets $G$ and $S$.

Homework 3 (Due Thursday 9/5)

• Read: Continue with Chapter 3 up through the end of Section 3.1
• Turn in: 3.20, 3.21, 3.22, 3.23, 3.24, 3.27

  Please make sure to start early as some of these may take a little more time. Take care in proving 3.24 as you are really proving a bi-conditional: $z$ is an $n$th root of unity iff $z$ is in $\{1,\zeta_n, (\zeta_n)^2,\ldots, (\zeta_n)^{n-1}\}$. But, one direction was proven in a previous problem. Also, you can use Theorem 3.26 for Problem 3.27 even though you are not being asked to prove 3.6. (Hopefully we'll have time to explore 3.25 and 3.26 in class together, but feel free to prove them now if you'd like.)

Homework 2 (Due Tuesday 9/3)

• Read: End of Chapter 2 and beginning of Chapter 3 up through Problem 3.18 (see our book)
• Turn in: 3.6, 3.9, 3.10, 3.11, 3.13, 3.14, 3.16, 3.17, 3.18

  Although I'm not asking you to prove 3.12, you are free to use it for later problems. In particular, you can us it for Corollaries 3.13 and 3.14.

Homework 1 (Due Thursday 8/29)

• Read: All of Chapter 1 and the beginning of Chapter 2 up through Section 2.1 (see our book)
• Turn in:
  1. Short paragraph about one aspect of an IBL approach that you view as positive and one concern that you have.
     (This is based off of the reading in Section 1.2.)
  2. Solutions to (or your best efforts on): Problems 2.1, 2.2, 2.4, 2.5, 2.7, 2.8, 2.9 (see Chapter 2 of our course book)

     On Problem 2.1, you will need to use a computational tool for some of the parts—WolframAlpha works well. Problems 2.2, 2.5, 2.7 are a bit vague. If you find them hard to understand, talk with your peers, and see if you can get at what they are asking. But, you should not spend too much time on them.

Writing Assignments

Other Handouts

Course Log

Finals Week
[12.12.19] - Thursday Last bit of working (and partying!) time together this semester. Happy break!!
What we did: Final Projecting
Week 15
[12.05.19] - Thursday Last day—sooo bittersweet! We discussed the connection between a polynomial $p(x)$ being solvable by radicals over $\mathbb{Q}$ and $\operatorname{Aut}(\mathbb{Q}^{p(x)}/\mathbb{Q})$ being a solvable group. We then went through the end game, showing ultimately that the polynomial $x^5 + 5x^4 - 5$ is NOT solvable by radicals over $\mathbb{Q}$. Cakes. Missing you all already, but happy we'll reconvene to work on the final project next Thursday. Good luck with everything!
What we covered: The end of Chapter 7 and The End Game
[12.03.19] - Tuesday It was hard coming back from break, but we covered some important material. Did a lot of the work as a team but were lucky to get treated to 2 presentations. Thanks presenters: Team110B, NC + SK, Team110B, Team110B, DM, Team110B
What we covered: 7.20, 7.21, 7.22, 7.23, 7.24, 7.28 (we skipped 7.29, 7.31, and 7.32 for now)
Week 14
[11.26.19] - Tuesday Got going on Galois extensions today. Thanks for all of the hard work y'all! Our presenters were: GH, TU, JB, JN, JS, IS, BT + HR
What we covered: 7.2, 7.3, 7.4, 7.7, 7.10, 7.11, 7.17 (we skipped 7.18)
Week 13
[11.21.19] - Thursday More work with automorphism groups of fields, with cameos by $\mathbb{Z}_2$, $\mathbb{Z}_4$, and $V_4$. Thanks for a fun day you all! We're getting close! Today's awesome presenters were: AF, AA + AG + CE, DM, KP, team 110B, MP
What we covered: 6.72, 6.74, 6.76, 6.77, 6.79, 6.80
[11.19.19] - Tuesday Collected the exam and then lectured over isomorphisms and automorphisms of fields.
What we covered: most of 6.66–6.73
Week 12
[11.14.19] - Thursday More work on field extensions and then transitioned to isomorphisms of fields. Ended by handing out the next exam—good luck!! Thanks presenters: AE, AF, IM, JB, DB, HF
What we covered: 6.50, 6.60, 6.61, 6.62, 6.64(1), 6.65 (we skipped 6.63 and part 2 of 6.64)
[11.12.19] - Tuesday Worked a lot on finding bases for and degrees of field extensions today. Among other things, we finally saw that $\mathbb{Q}(\sqrt{2} + i) = \mathbb{Q}(\sqrt{2},i)$, which a long time in the making. It was a very colorful day (see below)! Thanks all! And special thanks to the presenters: MP, AG, CE + AA, SK, BT, NB + HR, MDS. Apologies to MDS for not getting to the last problem—a photo is below.
What we covered: 6.42, 6.43, 6.45, 6.47, 6.49, 6.51, 6.55 (we skipped 6.48)
Week 11
[11.07.19] - Thursday Continued working with Eisenstein's Irreducibility Criteria today and, among other things, showed that the minimal polynomial for $\zeta_5$ over $\mathbb{Q}$ is $x^4+x^3+x^2+x+1$. We ended with a little linear algebra. Thanks presenters: TU, JN, EO, MKH, JW, GH.
What we covered: 6.28, 6.29, 6.30, 6.31, 6.39, 6.41
[11.05.19] - Tuesday Achieved our desired "nice description" of the elements of $F(\alpha)$ and applied it to several examples. We also added a test for irreducibility to tool box: Eisenstein's Irreducibility Criteria. Fun day—thanks you all! Today's presenters were: JW, NC, YR, GK, YR, MDS, MDS, GH
What we covered: 6.17, 6.18, 6.20, 6.21, 6.23, 6.24, 6.26, 6.27 (we skipped 6.22)
Week 10
[10..19] - Thursday Continued our work on algebraic elements by looking at minimal polynomials and getting started on trying to find a nice description of fields of the form $F(\alpha)$. Great presentations and lots of productive conversations! Thanks you all, especially presenters: HR, TU, KP, JB, DM, MKH, IS. Happy Halloween!
What we covered: 6.5, 6.9, 6.10, 6.11, 6.12, 6.14, 6.16 (we skipped 6.17)
[10.29.19] - Tuesday I started by lecturing over 5.115 and 5.118, which we had skipped last time. The 5.118 discussion was then woven into 5.125 from this time. We then worked through 5.120 and 5.122 together before turning it over to MP for 6.2 and IM for 6.3 + 6.4. Sorry for all of the lecturing today—we'll get back to normal next time.
What we covered: 5.115, 5.118, 5.120, 5.122, 5.125, 6.2, 6.3, 6.4 (we skipped 5.123 and 6.5)
Week 9
[10.24.19] - Thursday Homomorphisms (and kernels and images) today. There was a lot to wrap our heads around, and we had really good discussions...though again, we didn't get to everything. Thanks presenters: AF + JW, AF + JW, EY, EO, JW + AE, HF
What we covered: 5.107, 5.108, 5.110, 5.112, 5.114, 5.115, 5.117(1), 5.118 (we skipped 5.115, 5.118)
[10.22.19] - Tuesday Investigated principal ideals today. Lots of good problems, but again, we didn't get to them all Today's presenters were: AG, IM + JN, AA, BT, GK, NB, HR
What we covered: 5.87, 5.90, 5.96, 5.99, 5.100, 5.104, 5.105 (we skipped 5.98)
Week 8
[10.17.19] - Thursday Crushing ideals and quotients today! These concepts can be quite challenging (especially quotients!), but it seems like we are off to a good start. Lot's of great problems today, but unfortunately we didn't get to talk through them all. Pictures of the two we missed are below—sorry IM and BT!! Today's presenters were: NC, DB, AE, SK, IM, BT
What we covered: 5.78, 5.79, 5.82, 5.83, 5.85, 5.86 (we skipped 5.80)
[10.15.19] - Tuesday More work on irreducibility today and also started transitioning back to general ring theory with subrings and ideals. Thanks all! Today's presenters were: JW, JS, AE, KP + NB, MKH, EO + DB, YR
What we covered: 5.61, 5.64, 5.65, 5.66, 5.68, 5.71, 5.77 (we skipped 5.72)
Week 7
[10.10.19] - Thursday Back to you all presenting today—so nice! Worked through GCD and the beginnings of irreducibility. Thanks presenters: BT, SK, HF, HR + JS, DB, JW, GK
What we covered: 5.46, 5.52, 5.53, 5.55, 5.58, 5.59, 5.62
[10.08.19] - Tuesday Turned in the take-home exam today. Then I got to do some math, discussing the division algorithm and the beginnings of GCD.
What we covered: 5.37, 5.41, 5.43, 5.44, 5.45, 5.47, 5.48
Week 6
[10.03.19] - Thursday More examples of rings today: matrix rings and polynomial rings. Polynomials were really our motivation for investigating rings, and next up is to dive deeper into the theory of polynomial rings. Thank all! Today's excellent presenters were: AE, NB, JB, GK, SK, NC, GH, TU. Also, the first midterm was handed out today—good luck!
What we covered: 5.24, 5.25, 5.27, 5.28, 5.30, 5.32, 5.35, 5.36
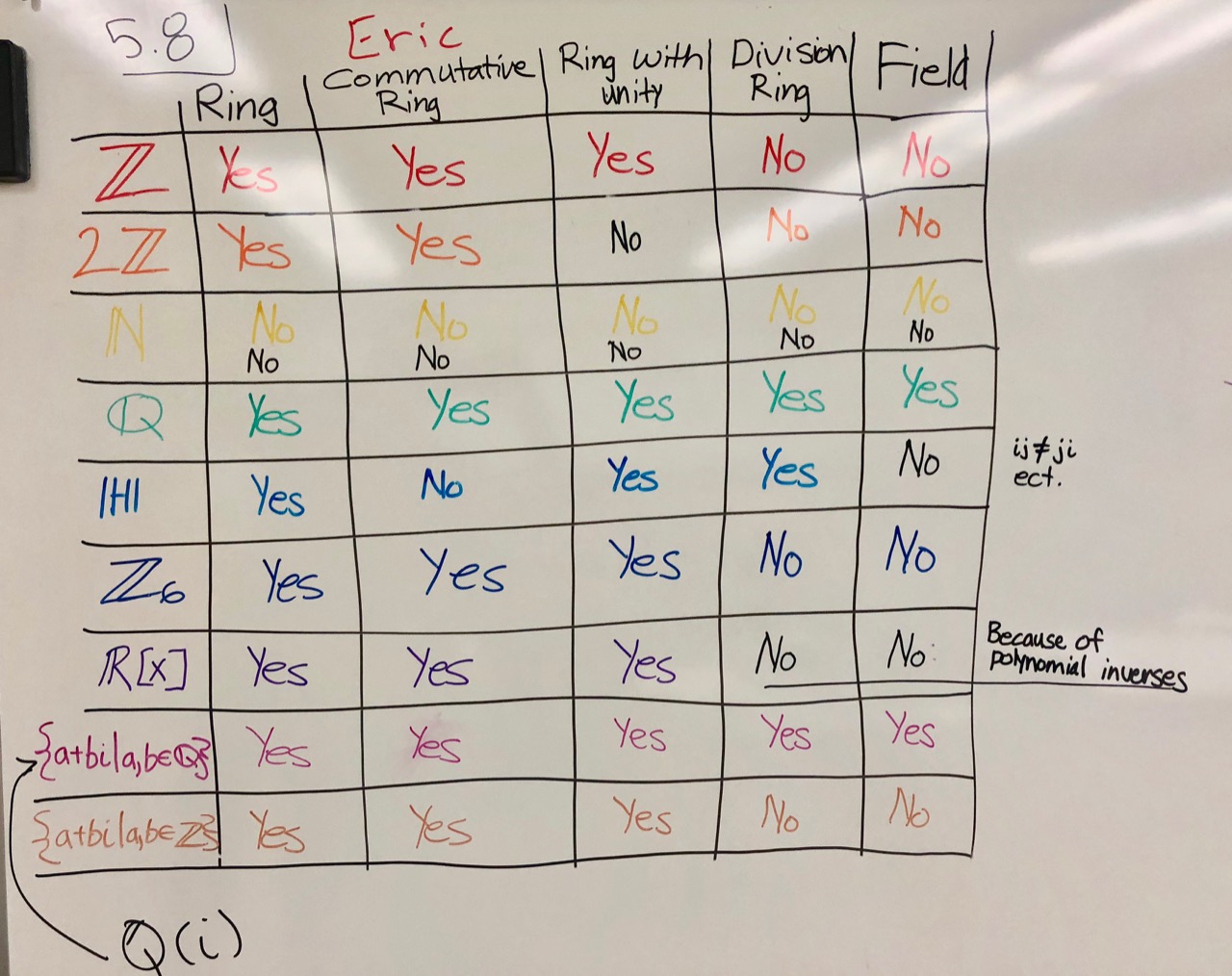
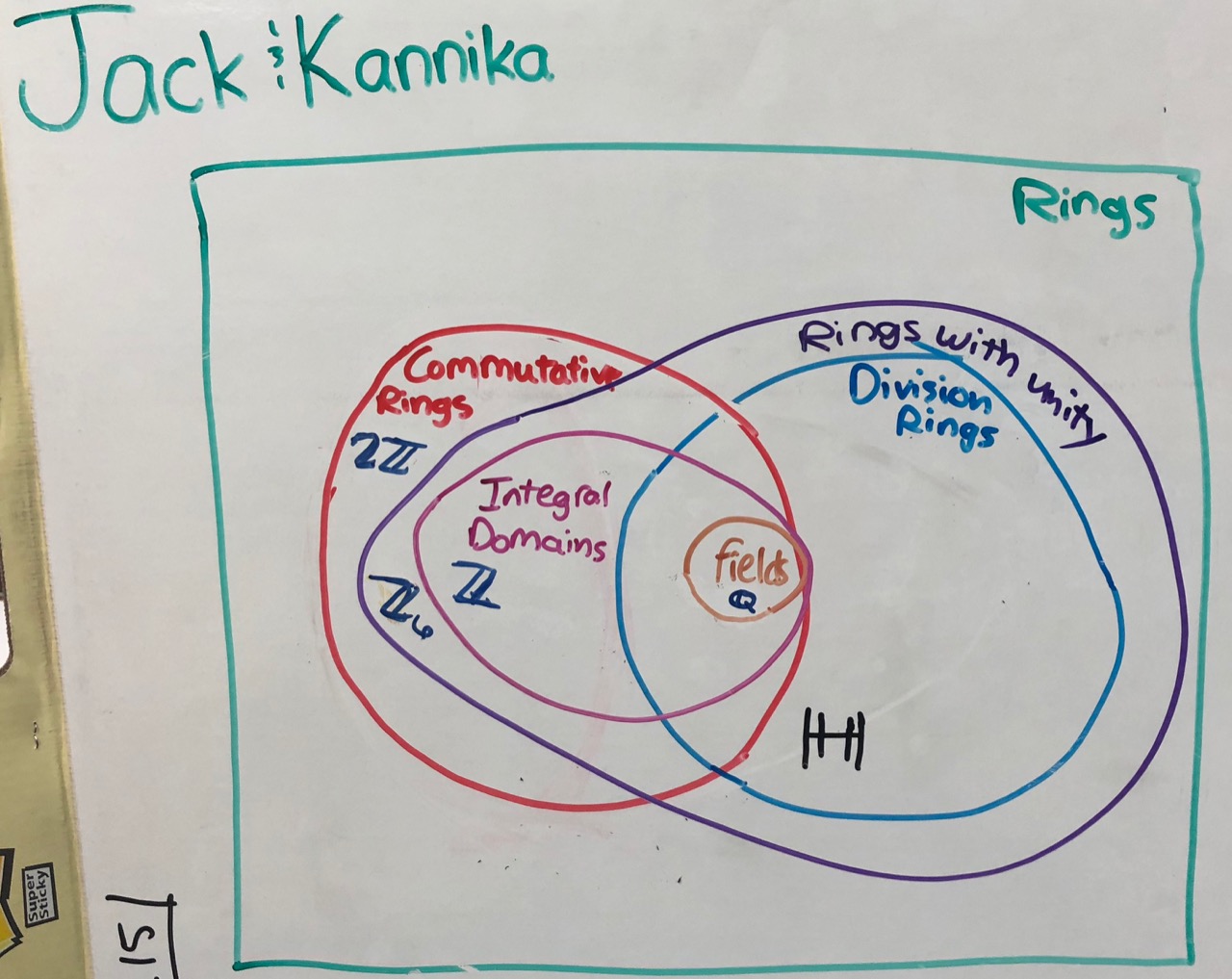
[10.01.19] - Tuesday Got going with abstract rings today, exploring several different definitions and cataloging some first examples (see below). Thank to everyone, especially presenters: EO, YR+MDS, AA, JB+KP, CE, AG, DM.
What we covered: 5.8, 5.12, 5.13, 5.15, 5.17, 5.18, 5.19, 5.20
Week 5
[09.26.19] - Thursday We saw several polynomials that are solvable by radicals today. For the rest of the course, we will be looking for one that is not. We also got started on rings as we explored some of the poperties of polynomials. Thanks presenters: HR, MDS, NC, IS, AF, BT!
What we covered: 4.12, 4.13, 4.14, 5.2, 5.3, 5.4.
[09.24.19] - Tuesday Radical extensions and solvability by radicals today! ...so many definitions. Great presentations and nice discussions today! Thank to all, especially the presenters: AF, DM, GH, YR, JN, HF + MKH, IM.
What we covered: 4.3, 4.4, 4.6, 4.8, 4.9, 4.10, 4.11.
Week 4
[09.19.19] - Thursday Spent more time wrapping our head around adjoining elements to fields, which seems to be getting clearer. Nice job to all! And many thanks to the presenters: Me, TU, MP + DB, GK, CE, JN, EO.
What we covered: 3.66 , 3.67, 3.68, 3.69, 3.70 + 3.71, 3.72, 3.73.
[09.17.19] - Tuesday Lot's of math to cover today, and we didn't quite get there. Sorry for the rush! We'll make sure to revisit several of the problems when we meet on Thursday. Thanks presenters (even though we didn't get to everyone ☹): AG, IM, IS, HF + EY + DB, JS, EY, Me, AE.
What we covered: 3.51, 3.53, 3.56, 3.57, 3.58, 3.62, 3.64, 3.65.
Week 3
[09.12.19] - Thursday Lot's of presentations (and great discussion!) today as we got started on fields. Thanks you all!! Today we had presentations from : JB, GH + CE + EY, NB + SK, HF + HR + MKH + MP.
What we covered: 3.43, 3.44, 3.45, 3.47, 3.48, 3.50 (1,2,3,4).
[09.10.19] - Tuesday Hamiltonians today as well as an investigation of $\mathbb{Q} + \mathbb{Q}\sqrt{5}$. Fun math and fun conversations! Thanks all around, especially to the presenters: NC, AF + AA, MDS, JS, EO ,IS, YR.
What we covered: 3.25, 3.33, 3.34, 3.37, 3.38, 3.39, 3.40. (We skipped 3.36.)
Week 2
[09.05.19] - Thursday Hard problems today and great discussion! Thanks y'all! And extra !yay! to the presenters: DM + SK, AE, AG, HR, JS.
What we covered: 3.20, 3.21, 3.22, 3.23, 3.24, 3.27.
[09.03.19] - Tuesday Lots about complex numbers today, with many nice proofs and several great pictures (which you know I love!). Thanks to everyone for an excellent day, with special thanks to the presenters: JN, TU + EY, GK, NC, BT, NB, YR, KP, MKH.
What we covered: 3.6, 3.9, 3.10, 3.11, 3.13, 3.14, 3.16, 3.17, 3.18.
Week 1
[08.28.19] - Thursday More about solving polynomials today, ending with a discussion about where we are headed in the course: there is no "quintic formula"! Thanks to you all for a fun day, especially the presenters: MP, BT, KP, HF.
What we covered: Last four parts of 2.1, 2.4, 2.8. We also talked through 2.2, 2.5, 2.8, and 2.9.
[08.26.19] - Tuesday - First day! So great to meet you all! We covered a lot of ground setting the stage for the course, and even got to some math at the end. Thanks to DB and IM for the presentations!
What we covered: First four parts of Problem 2.1