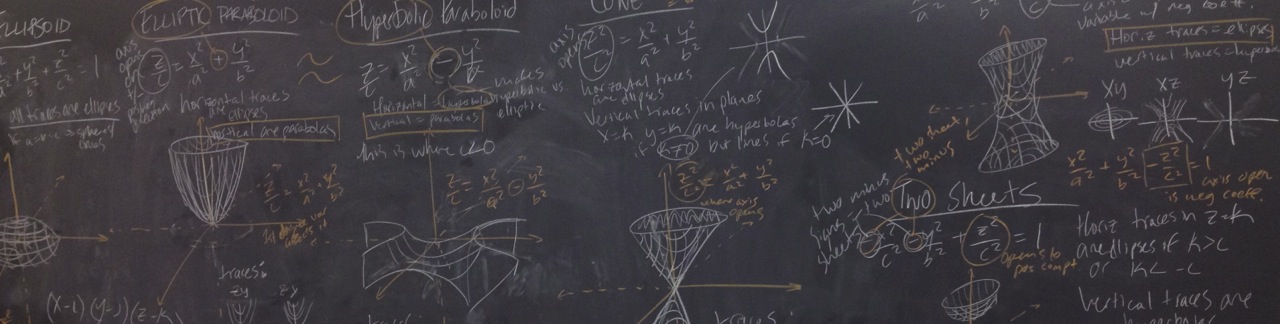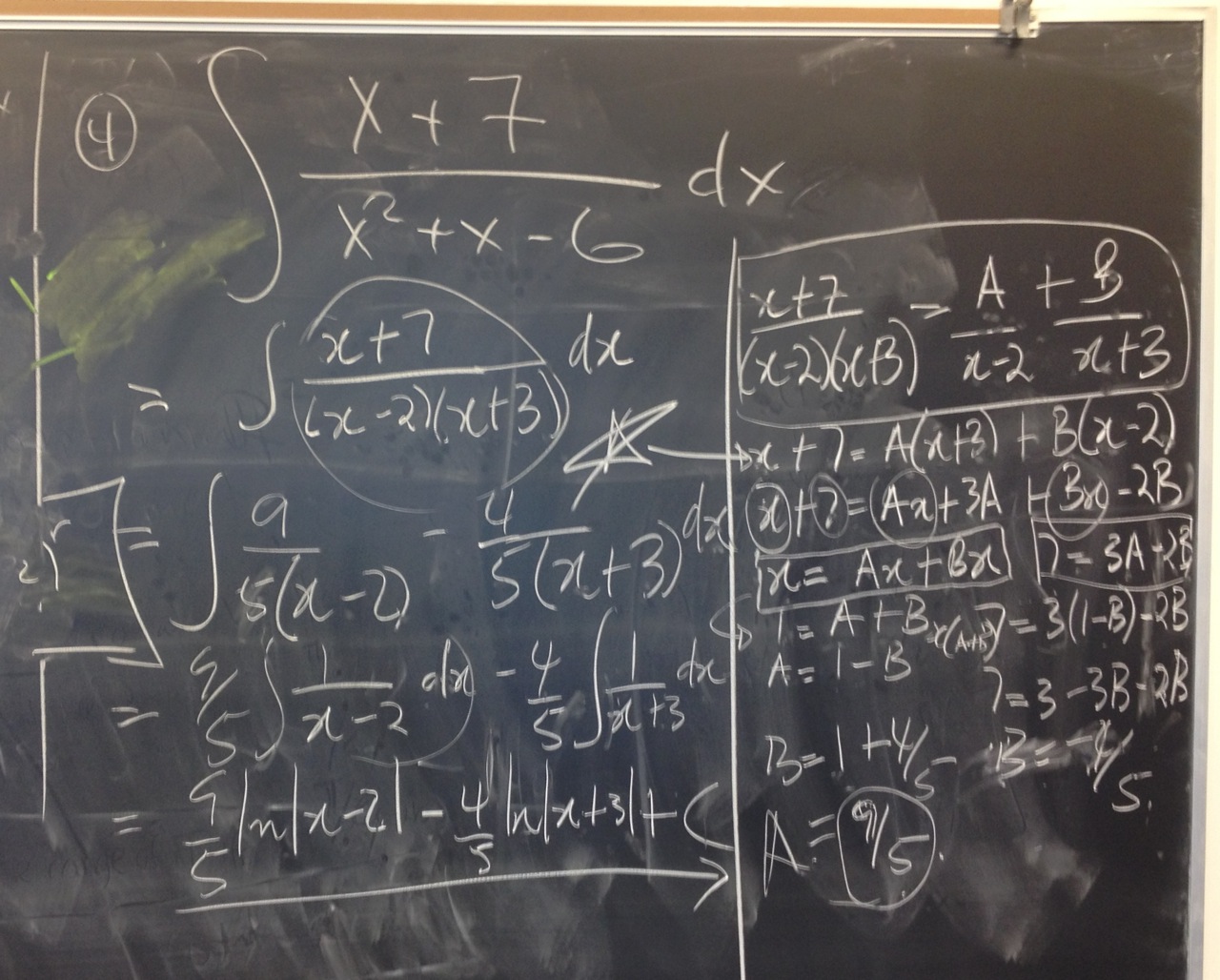| Week 1 |
|---|
|
[08.28.15] - Friday - First day!
|
|


- Some of the important topics we covered. -
|
|
Sections covered: 5.2 (started)
|
Reading for next time: Section 5.2 (and 5.1 if you need to fill in). Focus on the following:
- the definition of the definite integral, and
- the content in blue boxes, e.g. statements of theorems and properties of the definite integral.
|
To discuss next time:
- Where should Rich from the CarTalk Problem mark for 3/4 tank of gas? Hint: this is hard! If you don't fully solve it, that is fine, but make sure you can clearly explain your approach and where you got stuck. Make sure to indicate if you use outside resources for parts of your solution, e.g. Desmos or WolframAlpha.
|
| Week 2 |
|---|
|
[08.31.15] - Monday The CarTalk discussion was fantastic! Thanks for all of the participation, and extra thanks to all those that went to the board!
|
|
Sections covered: 5.2 (finished), 4.4 (started)
|
|

- CarTalking. -
|
Reading for next time: Section 4.4. Focus on the following:
- L'Hospital's Rule (pg. 305, blue box)
- Examples 1, 2, 3, and 6.
Don't forget that there's Homework (written and online) due Tuesday!
|
To discuss next time:
- CarTalk again: where should Rich from the CarTalk Problem mark for 3/4 of a tank of gas? Make sure you understand the reformulation of the problem (using a definite integral) that was presented today, and try to "solve" the CarTalk problem, i.e. make as good of an estimate as you can as to where the 20 inch stick should be marked for 3/4 of a tank of gas.
- Try to find the error in the following argument; it is wrong!
I want to find $\lim_{x\rightarrow \infty} \frac{x+\sin x}{x}$. As $x\rightarrow \infty$, both the top and bottom of the fraction tend to $\infty$, which yields an indeterminate form of the type $\frac{\infty}{\infty}$. Using L'Hospital's Rule, I find that $\lim_{x\rightarrow \infty} \frac{x+\sin x}{x} = \lim_{x\rightarrow \infty} \frac{1+\cos x}{1} = \lim_{x\rightarrow \infty} (1+\cos x)$. As $x\rightarrow \infty$, $(1+\cos x)$ oscillates between $0$ and $2$, so $\lim_{x\rightarrow \infty} (1+\cos x)$ does not exist. Thus, $\lim_{x\rightarrow \infty} \frac{x+\sin x}{x}$ does not exist.
It may be best to first figure out the correct answer to $\lim_{x\rightarrow \infty} \frac{x+\sin x}{x}$. Hint: graph it! The limit exists.
|
|
[09.02.15] - Wednesday Two more great presentations today! (But I forgot to take a pic...)
|
|
Sections covered: 4.4 (continued)
|
Reading for next time: End of Section 4.4 and Section 6.2. Focus on the following:
- The final part of 4.4 about "Indeterminate Powers"
- Example 1 in 6.2
Don't forget that there's Homework (written and online) due Friday!
|
To discuss next time:
- Write down a step-by-step process to follow when trying to deal with indeterminate powers. Illustrate how to use your process as you solve \[\lim_{x\rightarrow \infty} \left(1+\frac{1}{x}\right)^x\]
- Given a ruler and a knife, can you find a good estimate of the volume of an eggplant? Be prepared to demonstrate.
|
|
[09.04.15] - Friday Three excellent presentations today - pics below! The eggplant never stood a chance...

- Indeterminate powers - Yay $e$! -


- We just had to know: 30.26 cubic inches -
|
|
Sections covered: 6.2 (started)
|
Reading for next time: End of Section 6.2 and Section 6.3. Focus on the following:
- Example 3 and 5 in 6.2. (We did Example 7 in class today. Look in the book for a better picture than I put on the board.)
- The intro. to 6.3 up through Example 1
|
To discuss next time:
- Find the volume of Gabriel's Horn. Gabriel's Horn is the solid obtained by revolving the graph of $y=\frac{1}{x}$, from $x=1$ to $\infty$, about the $x$-axis. Hint: first find the volume of the horn from $x=1$ to $x=a$, and then take the limit as $a\rightarrow \infty$. Be prepared to present a picture and explain the the integral that you came up with, as well as the limit.
|
| Week 3 |
|---|
|
[09.07.15] - Monday Lots of volumes today!! ...and saw a very nice presentation that the infinitely long Gabriel's Horn has a finite volume (of $\pi$)!
|
|
Sections covered: 6.2 (finished), 6.3
|
Reading for next time: Section 7.1. Focus on the following:
- the introduction and formula for integration by parts, i.e. every thing before Example 1
- Examples 1, 2, 3
Don't forget that there's Homework (written and online) due Tuesday!
|
To discuss next time:
- Find the volume of the solid obtained by revolving the region bounded by $y=e^x$, $y=0$, $x=0$, and $x=1$ about the $y$-axis. Hint: graph it first. What seems easier: shells or washers? Or maybe they both seem hard. And now the real hint: you will likely need to use integration by parts to finish things off.
|
|
[09.09.15] - Wednesday A bit more volume today, via two nice presentations, which ended with a hook into integration by parts (and a lot more examples).
|
|
Sections covered: 7.1
|
Reading for next time: Section 7.2. Focus on the following:
- Examples 1 - 4
Don't forget that there's Homework (written and online) due Friday!
|
To discuss next time:
- We will start with a quiz. I will ask you set-up (but not evaluate) an integral that computes a particular volume, and I will also ask you to do a problem very similar to Example 1 in 7.2.
- Meditate (again) on the discussion question from last time about the volume of the solid obtained by revolving the region bounded by $y=e^x$, $y=0$, $x=0$, and $x=1$ about the $y$-axis. What does the integral look like if you use washers instead of shells? Can you comute the resulting integral?
|
|
[09.11.15] - Friday One quiz, two great, colorful presentations (one pictured below), and a whole lot of trig.

|
|
Sections covered: 7.2
|
Reading for next time: Section 7.3. Focus on the following:
- The introduction
- Examples 1 and 3
Don't forget that there's Homework (written and online) due today!
|
To discuss next time:
- When trying integration by parts, describe how you choose which function is $u$ (and which is part of $dv$). In class, we decided that, first and foremost, we need to be able to integrate $dv$, and we also hope that our choice for $u$ becomes "simpler" after differentiation. Can you be more specific? For example, suppose that one of the pieces is an inverse trig. function; would you make it part of $u$ or $dv$? What if you encounter a logarithmic function?
- CarTalk! Use what you read in Section 7.3 to compute $\int \sqrt{100 - x^2}\, dx$.
|
| Week 4 |
|---|
|
[09.14.15] - Monday So...much...trig!
|
|
Sections covered: 7.3
|
Reading for next time: Section 7.4. Focus on the following:
- Introduction through Example 2
Don't forget that there's Homework (written and online) due Tuesday!
|
To discuss next time:
- You know how to compute $\int \frac{1}{x-6}\;dx$, right?
- Using what you read in 7.4 (Example 1), compute $\int \frac{x^2+x+1}{x-6}\;dx$.
- Remember how to compute $\int \frac{4x+2}{x^2+x-6}\;dx$? Hint: basic substitution.
- Using what you read in 7.4, try to compute $\int \frac{x+7}{x^2+x-6}\;dx$.
|
|
[09.16.15] - Wednesday So...much...algebra!
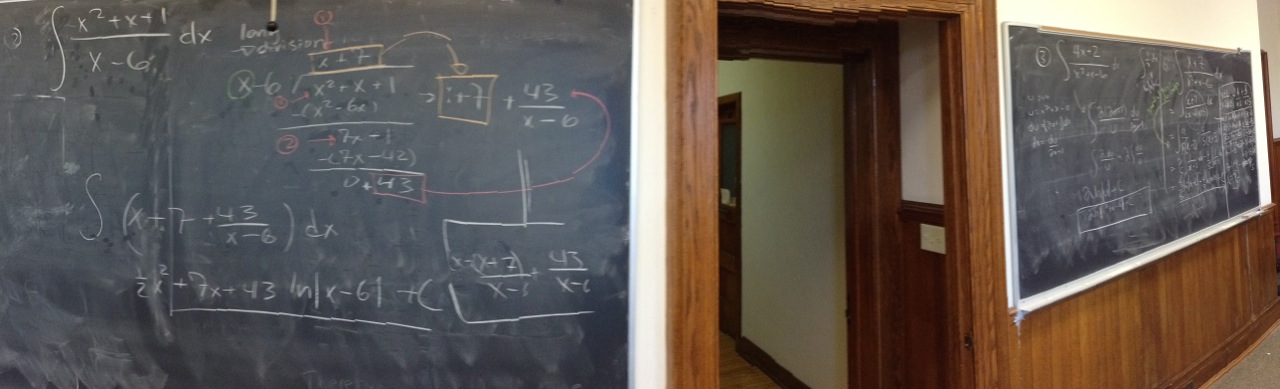
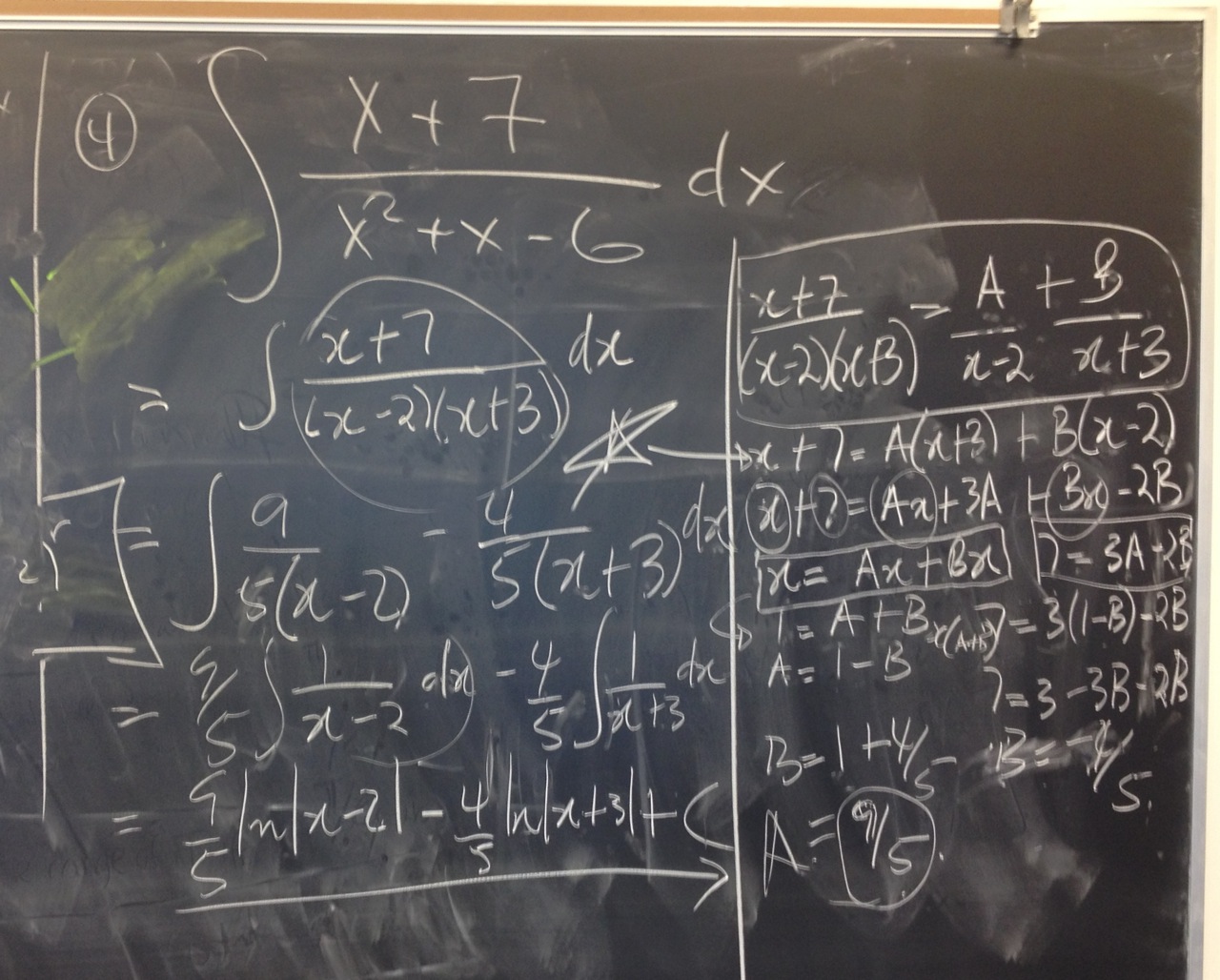
- You all clearly don't need me! Nice job! -
|
|
Sections covered: 7.4 (started)
|
Reading for next time: End of Section 7.4. Focus on the following:
- Examples 7-9
Don't forget that there's Homework (written and online) due Friday!
|
To discuss next time:
- Be prepared to write out the form of the partial fraction decomposition (as in Example 7) for any big, nasty rational function, but you can assume that the denominator will be easy to factor.
- Using what you read (in Example 9), try to compute $\int \frac{dx}{x^2+x\sqrt{x}}\;dx$.
|
|
[09.18.15] - Friday Very nice presentations and great discussion today. We started improper integrals at the end and had fun meditating on the fact that $\int_1^\infty \frac{1}{x^2}\,dx = 1$ while $\int_1^\infty \frac{1}{x}\,dx = \infty$.
|
|
Sections covered: 7.4 (finished), 7.8 (started)
|
Reading for next time: End of Section 7.8. Focus on the following:
- Examples 5-7
|
To discuss next time:
- True or False: $\displaystyle\int_{-1}^1 \frac{1}{\sqrt[3]{x}}\,dx = 0$. Explain.
|
| Week 5 |
|---|
|
[09.21.15] - Monday Great presentations today. I love seeing the successes and the failures!
|
|
Sections covered: 7.8 (finished), 8.1 (started)
|
Reading for next time: Section 8.1. Focus on the following:
- Introduction through Example 2
Don't forget that there's Homework (written and online) due Tuesday!
|
To discuss next time:
- Set up an integral to compute the length of $y=\sin(x)$, $0\le x\le 2\pi$. Can you evaluate this integral? If you can, do it; otherwise, estimate it using a Riemann sum (with not too many rectangles).
- Set up an integral to compute the length of $y=\ln|\cos(x)|$, $0\le x\le \frac{\pi}{3}$. Can you evaluate this integral? If you can, do it; otherwise, estimate it using a Riemann sum (with not too many rectangles).
|
|
[09.23.15] - Wednesday Three excellent presentations today. The board looked gorgeous, and I totally failed to take a picture... Next time. Nice job everyone!
|
|
Sections covered: 7.8 (finished, again), 8.1 (finished), 8.2 (started)
|
Reading for next time: Section 8.2. Focus on the following:
- Introduction through the blue box labeled $\fbox{4}$
- Example 1
|
To discuss next time:
- Set up an integral that computes the surface area of Gabriel's Horn. (Recall that Gabriel's Horn is the solid obtained by revolving the graph of $y=\frac{1}{x}$, from $x=1$ to $\infty$, about the $x$-axis.)
- Show that the integral diverges. Hint: try a comparison test.
|
|
[09.25.15] - Friday Another nice set of presentations, and another failed photo op. I swera I'll remember next time...probably.
|
|
Sections covered: 8.2 (finished), 10.1 (started)
|
Reading for next time: Section 10.1. Focus on the following:
- Introduction
- Examples 1, 2, 4
|
To discuss next time:
- Play around with parametric equations in Desmos. Look at the following for examples:
- Use Desmos and what you learned in Example 4 to do problem 35 on page 647 of the textbook. Write everything down on paper, so you can reproduce it in class. Hint: each part of the picture will be represented by a different set of parametric equations.
- Use Desmos to make a super cool graph using parametric equations. Write everything down on paper, so you can reproduce it in class.
|
| Week 6 |
|---|
|
[09.28.15] - Monday Two great Desmos presentations today: Smiley and Mjölnir. The picture below is a mash up of the two; smiley was never in actual danger. Many thanks to the presenters!
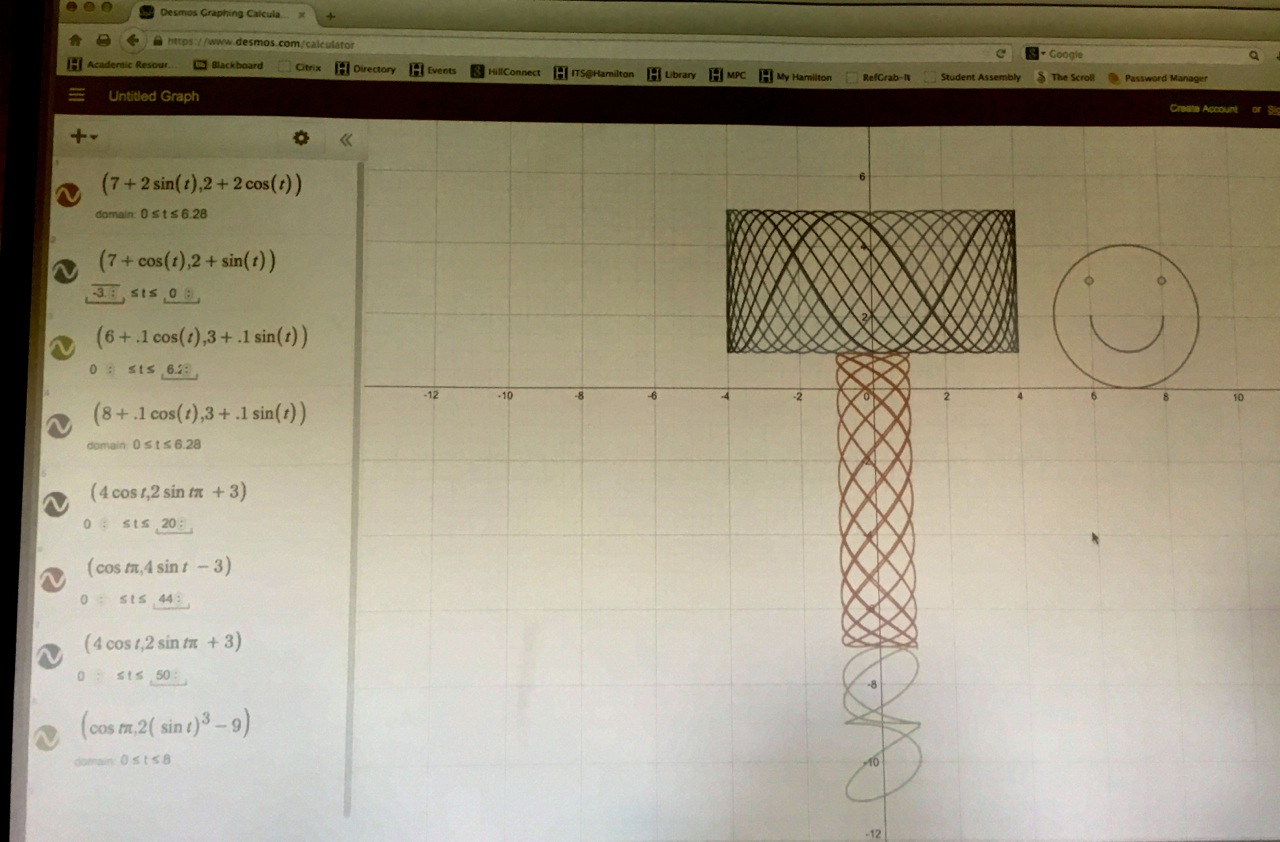
|
|
Sections covered: 10.1 (finished), 10.2 (started)
|
Reading for next time: Section 10.2. Focus on the following:
- Introduction through Example 3
Don't forget that there's Homework (written and online) due Tuesday!
|
To discuss next time: Consider the curve $\mathcal{C}$ defined by the parametric equations \[\begin{align*}x=& t^3-3t\\ y=& 3t^2-9\end{align*}\]
- Check out the graph of $\mathcal{C}$ here https://www.desmos.com/calculator/x7cia8bdpz. The graph also illustrates tangent lines.
- Determine all places where $C$ has horizontal tangent lines. The graph may guide you, but make sure you can write down the math to support your answer.
- Determine all places where $C$ has vertical tangent lines.
- Find equations for all lines tangent to $C$ at $(0,0)$.
- Find the area of the "teardrop" at the bottom of $C$. Hint: to find the area between a parametric curve $x=f(t)$, $y=g(t)$, $\alpha\le t\le \beta$, and the $x$-axis, the book gives the formula $\int_\alpha^\beta g(t)f'(t)\;dt$. Here it might be better to find the area between the curve and the $y$-axis, and for this, the formular is $\int_\alpha^\beta f(t)g'(t)\;dt$
|
|
[09.30.15] - Wednesday Very nice presentations today! And we now know the area of the teardrop: $\frac{72\sqrt{3}}{5}$.
|
|
Sections covered: 10.2
|
Reading for next time: Section 10.3. Focus on the following:
- Introduction
- Examples 1, 4, 5, 7
|
To discuss next time:
- Play around with polar equations in Desmos. Look at the following for examples:
- Use Desmos to make a super cool graph using a polar equation. Write everything down, so you can reproduce it in class.
- Graph the polar equation $r=\frac{\pi}{\theta}$. Make sure you zoom in enough to see the spiral and zoom out enough to see that it does not continue to spiral. Think about what $r$ and $\theta$ represent and be able to explain why the graph looks like it does.
|
|
[10.02.15] - Friday Started off with an example of computing the area of a suface obtained by revolving a parametrically defined curve, and then we launched into polar coordinates. We began with presentations of some fun polar pictures, though parts were drawn parametrically (in $xy$-coordinates) too. To truly appreciate the polar box, one has to realize just how wild of an animal a box is in the polar world. Nice job to both presenters! We then talked about the curve defined by $r=\frac{\pi}{\theta}$ (and I realized that I wasn't thinking about right myself). A brave voice got us studying the behavior as $\theta \rightarrow \infty$ and we also looked at what happens as $\theta \rightarrow 0^+$. Well done!
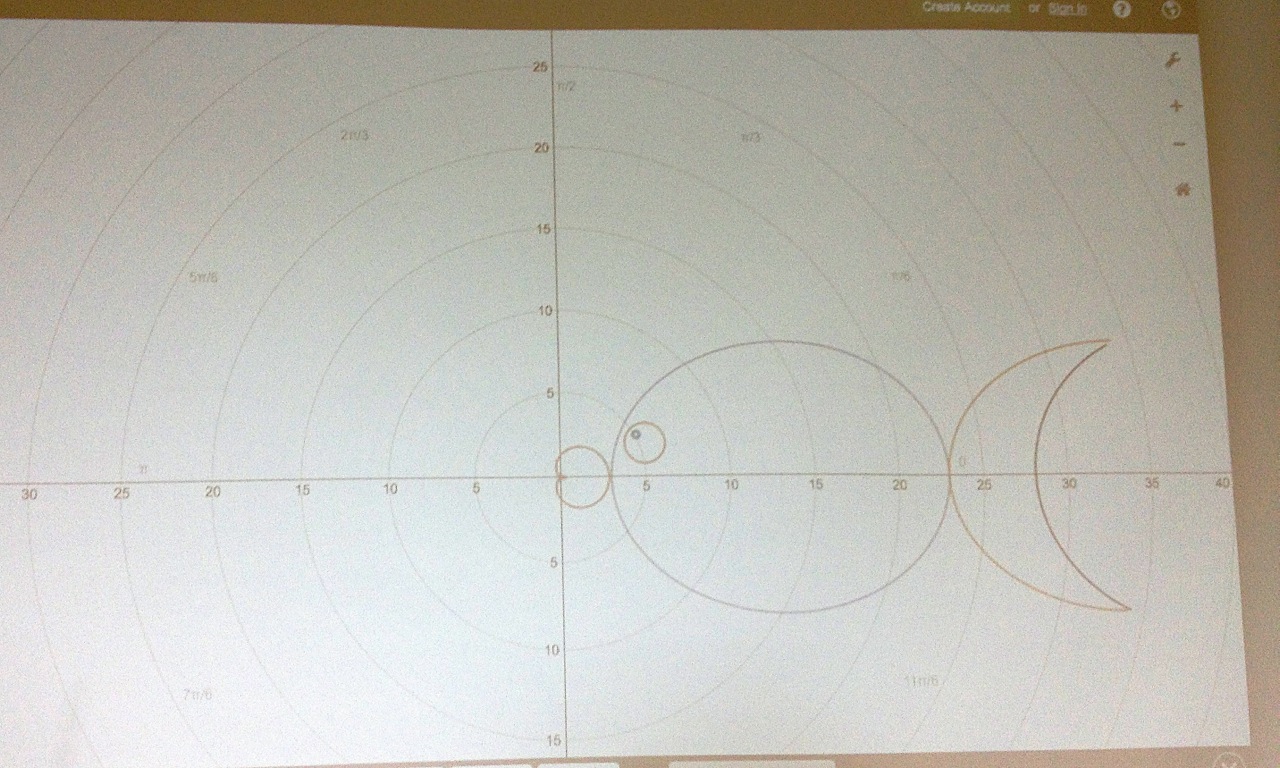 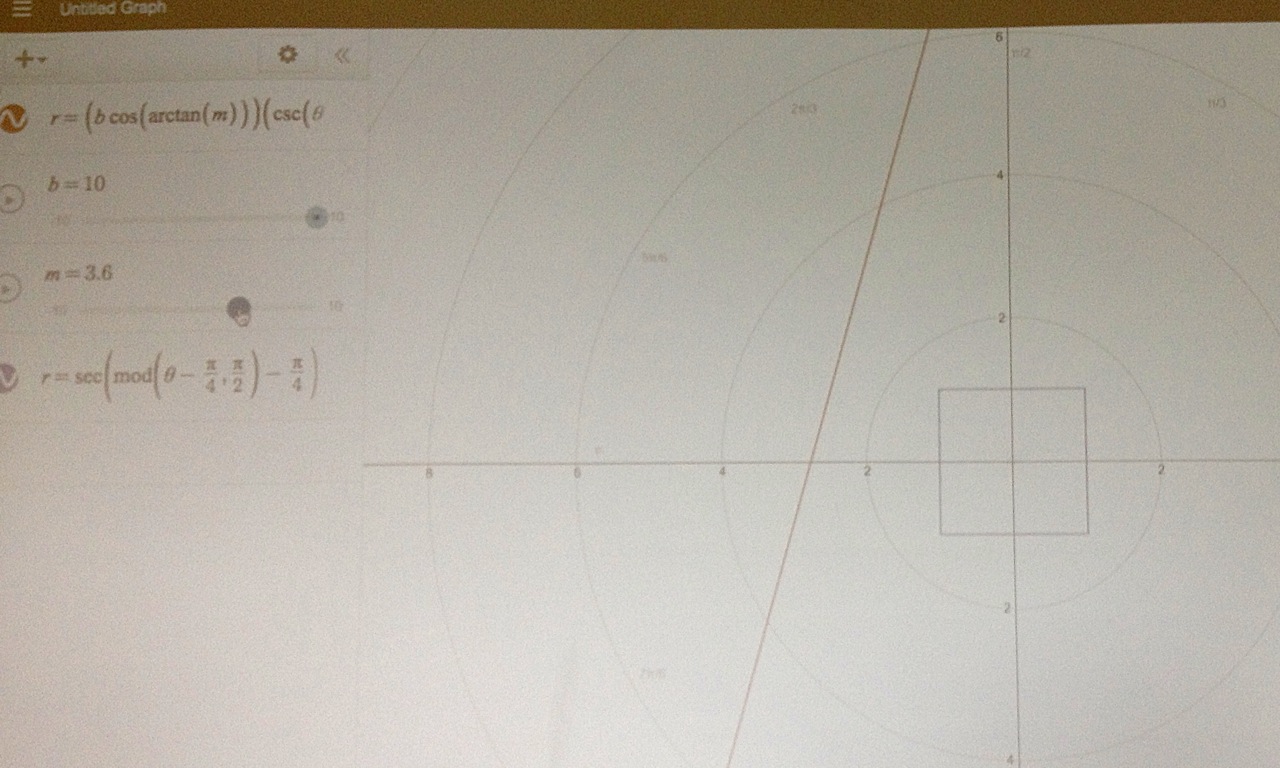
- Some wild polar animals -
|
|
Sections covered: 10.2 (finished), (10.3 started)
|
Reading for next time: Section 10.3. Focus on the following:
- The subsection "Tangents to Polar Curves" on pg 663
- Example 9
|
To discuss next time: Think more about the polar equation $r=\frac{\pi}{\theta}$.
- Graph it on Desmos, and study what happens when $\theta \rightarrow 0^+$.
- There seems to be a horizontal asymptote. Can you confirm this? Try using our conversion formulas and studying what happens to the $y$-values as $\theta \rightarrow 0^+$.
- Here's another approach. First compute $\frac{dy}{dx}$ for this curve. Now compute $\lim_{\theta \rightarrow 0^+} \frac{dy}{dx}$. What does this mean?
|
| Week 7 |
|---|
|
[10.05.15] - Monday
|
|
Sections covered: 10.4
|
Reading for next time: None. Start reviewing for the exam, which will cover up through Section 10.2.
Don't forget that there's Homework (written and online) due Tuesday!
|
To discuss next time: Let's start reviewing for the exam...
- Decide which section was the most challenging for you. Meditate on the following, and be prepared to share your answers (especially those who have not presented yet).
- What is an example of a problem from the section that you found challenging?
- What do you feel are the key parts of this problem that you need to understand better?
- Decide which section was the easiest for you. Meditate on the following, and be prepared to share your answers.
- What is an example of a problem from the section?
- What do you feel are the key parts of this problem that your classmates should be aware of so that it becomes easy for them too?
|
|
[10.07.15] - Wednesday Wrapped-up polar today, and then started reviewing for the exam. We discussed several problems, but below is one we didn't make it to. Try it; it's a good one!
Find the volume of the solid obtained by revolving the region bounded by the curves $y=x\ln x$, $x=e$, and $y=0$ about the $y$-axis. Be aware: part of the region is below the $x$-axis, so if you use shells, you need to split up the integral and "make that part positive."
|
|
Sections covered: 10.4 (finished), review for Midterm 1
|
Reading for next time: None. Focus on studying.
Don't forget that there's Homework (only written) due Friday!
|
|
To discuss next time: The exam.
|
|
[10.09.15] - Friday Started in on sequences today. Did a little group work and had a generally nice and lite day, well almost...
|
|
Sections covered: 11.1 (started)
|
Reading for next time: 11.1. Focus on the following:
- Definition 10, Example 12, Definition 11
- Theorem 12 and Figure 12 (you do not need to understand the proof of Theorem 12)
- Example 14 (beginning and end - the middle, which proves why the sequence in bounded, can be skipped)
|
To discuss next time: The golden ratio and continued fractions. Specifically, we will make sense of the following continued fraction:
\[1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1+\ddots}}} \]
The point is that the continued fraction really represents the limit of a particular sequence. Consider the following sequence (defined recursively - see Example 14): \[a_{n+1} = 1+\frac{1}{a_n},\quad a_1 = 1.\]
- Write down and do not simplify $a_1$, $a_2$, $a_3$, and $a_4$. Can you see why (and are you able to explain why) it makes sense to represent $\lim_{n\rightarrow\infty} a_n$ as the continued fraction above?
- Explain why $\{a_n\}$ is bounded below by $0$ and above by $2$.
- Now, $\{a_n\}$ is neither increasing nor decreasing, but it still can be shown that $\{a_n\}$ has a limit $L$. That is, $\lim_{n\rightarrow\infty}a_n = L$, but this also means that $\lim_{n\rightarrow\infty}a_{n+1} = L$. Use the method at the end of Example 14 to find $L$.
|
| Week 8 |
|---|
|
[10.12.15] - Monday
|
|
Sections covered: 11.1
|
Reading for next time: 11.2. Focus on the following:
- Intro through Example 4
- Example 9
|
To discuss next time: Section 11.2 introduces our first techniques for determining if series converge; let's discuss a couple of them.
- (Geometric series) After reading examples 2-4, try this variation: find the value of $c$ such that $\sum_{n=1}^\infty e^{nc} = 10$. How would your answer change if the equation was $\sum_{n=0}^\infty e^{nc} = 10$?
- (Harmonic series) Here's a different approach for showing that the series in Example 9 diverges.
- Check out this Demos graph: https://www.desmos.com/calculator/ufyuseeewk
- Explain why $\sum_{n=1}^\infty \frac{1}{n}$ can be thought of the blue area in the Desmos graph.
- Now explain why the blue area is infinite by showing that the blue area is greater than a different area that we know is infinite from much earlier in the course.
|
|
[10.14.15] - Wednesday
|
|
Sections covered: 11.2
|
Reading for next time: End of 11.2. Focus on the following:
- Example 8
- Theorem 8 (on page 714) through the end of the section
|
To discuss next time:
- After reading Theorem 8 and Example 11, determine if the following series is convergent or divergent: \[\sum_{n=1}^\infty \frac{2^n+e^n}{\pi^n}\]
- Meditate on Theorem 8, and be able to explain why the following is true:
If $\sum a_n$ is convergent and $\sum b_n$ is divergent, then $\sum (a_n + b_n)$ is divergent.
- Determine if the following series is convergent or divergent: \[\sum_{n=1}^\infty \frac{2^n+\pi^n}{e^n}\]
- Meditate on Theorem 8 again, and determine if the following is true or false:
If $\sum a_n$ is divergent and $\sum b_n$ is divergent, then $\sum (a_n + b_n)$ is divergent.
|
|
[10.16.15] - Friday Fall Break!
|
| Week 9 |
|---|
|
[10.19.15] - Monday
|
|
Sections covered: 11.2 (finished), 11.3 (started)
|
Reading for next time: 11.3. Focus on the following:
- The statement of the Integral Test on pg 721
- The (important) note between the statement of the Integral Test and Example 1 on pg 721
- Example 4
|
To discuss next time:
- After reading Example 4, determine if $\displaystyle\sum_{i=0}^\infty \frac{n}{e^n}$ converges or diverges.
- You will probably want to use the integral test, but to do this, make sure to explain why $\displaystyle\frac{x}{e^x}$ is continuous, positive, and (eventually) decreasing.
- Also, determine if $\displaystyle\sum_{i=0}^\infty \frac{-n}{e^n}$ converges or diverges.
|
|
[10.21.15] - Wednesday
|
|
Sections covered: 11.3 (finished), 11.4 (started)
|
Reading for next time: 11.4. Focus on the following:
- The blue boxes, i.e. the "Comparison Test" and the "Limit Comparison Test" (LCT)
- Note 1 and Example 2
- Note 2 and Example 3
|
To discuss next time:
- After reading the Comparison Test and LCT, think about the following questions about the series $\sum_{n=1}^\infty \frac{1}{n!}$.
- Explain why $\frac{1}{n!} \le \frac{1}{n}$ for $n\ge 1$.
- Explain why you cannot use the Comparison Test to compare $\sum_{n=1}^\infty\frac{1}{n!}$ to $\sum_{n=1}^\infty\frac{1}{n}$.
- Explain why $\frac{1}{n!} \le \frac{1}{n(n-1)}$ for $n\ge 2$.
- Show that $\sum_{n=1}^\infty\frac{1}{n(n-1)}$ converges by comparing it to an appropriate $p$-series. Were you able to use the Comparison Test or did you have to use the LCT?
- What can you conclude about $\sum_{n=1}^\infty \frac{1}{n!}$? And why?
|
|
[10.23.15] - Friday Great day, with lots of fantastic presentations (and lots of participation from the audience)! We'll pick up with the examples we ended with next time.
|
|
Sections covered: 11.4
|
Reading for next time: Reread 11.4. Focus on the following:
- The "Limit Comparison Test" (LCT)
- Example 4
|
To discuss next time:
- Think about the following questions related to $\sum_{n=1}^\infty \sin\left(\frac{1}{n}\right)$.
- Explain why $\sin\left(\frac{1}{n}\right)$ is positive for $n\ge 1$.
- Explain why you cannot use the Comparison Test to compare $\sum_{n=1}^\infty \sin\left(\frac{1}{n}\right)$ to $\sum_{n=1}^\infty\frac{1}{n}$. (A graph may help.)
- Show that you can use the LCT to compare $\sum_{n=1}^\infty \sin\left(\frac{1}{n}\right)$ to $\sum_{n=1}^\infty\frac{1}{n}$.
- Think about the following questions related to $\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n}$.
- Explain why you cannot use the Comparison Test to compare $\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n}$ to $\sum_{n=1}^\infty\frac{1}{n}$.
- Explain why you cannot use the LCT to compare $\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n}$ to $\sum_{n=1}^\infty\frac{1}{n}$.
- What's your feeling about the convergence or divergence of $\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n}$? Write this down, with your reasoning, before going to the next part.
- Look at the Desoms graph here: https://www.desmos.com/calculator/npezpry5vc. The orange dots represent the sequence of terms $\frac{(-1)^{n+1}}{n}$. The black dots represent the sequence of partial sums $s_n = \sum_{i=1}^n\frac{(-1)^{i+1}}{i}$. Did this change or confirm your feeling about convergence or divergence? If you want, you can compare the previous graph to the graph of the terms and partial sums of the harmonic series here: https://www.desmos.com/calculator/3vvosxcslp.
|
| Week 10 |
|---|
|
[10.26.15] - Monday
|
|
Sections covered: 11.5 (started)
|
Reading for next time: 11.6. Focus on the following:
- Definition 1 on page 737
- Example 2
- Theorem 3 on page 738
- Example 3
|
To discuss next time:
- Think about the following questions related to $\sum_{n=1}^\infty \frac{\sin\left(3^n\right)}{2^n}$.
- Explain why you cannot use the Comparison Test or LCT to compare $\sum_{n=1}^\infty \frac{\sin\left(3^n\right)}{2^n}$ to anything.
- Explain why the Alternating Series Test does not apply to $\sum_{n=1}^\infty \frac{\sin\left(3^n\right)}{2^n}$.
- Show that you can use the Comparison Test to compare $\sum_{n=1}^\infty \left\lvert\frac{\sin\left(3^n\right)}{2^n}\right\rvert$ to a convergent geometric series.
- What, if anything, does Theorem 3 on page 738 allow you to conclude about $\sum_{n=1}^\infty \frac{\sin\left(3^n\right)}{2^n}$?
|
|
[10.28.15] - Wednesday
Great discussions today! Thanks to everyone that participated, at the board and from the audience.
|
|
Sections covered: 11.5 (finished), 11.6 (started)
|
Reading for next time: 11.6. Focus on the following:
- The Root Test (blue box on page 741)
- Example 6
|
To discuss next time:
- Think about the following questions related to $\sum_{n=1}^\infty \left(\frac{n}{n+1}\right)^n$ and $\sum_{n=1}^\infty \left(\frac{n}{n+1}\right)^{n^2}$.
- Explain why the root test does not help you with $\sum_{n=1}^\infty \left(\frac{n}{n+1}\right)^n$.
- Compute $\lim_{x\rightarrow \infty}\left(\frac{x}{x+1}\right)^x$. Take your time with this. It requires equal parts logarithms and L'Hospital.
- What does the limit you found above tell you, if anything, about $\sum_{n=1}^\infty \left(\frac{n}{n+1}\right)^n$?
- What does the limit you found above tell you, if anything, about $\sum_{n=1}^\infty \left(\frac{n}{n+1}\right)^{n^2}$? Hint: root test.
|
|
[10.30.15] - Friday
Another great day of presentations and discussions!
|
|
Sections covered: 11.6 (finished)
|
Reading for next time: 11.7. Focus on the following:
- Read everything (including the examples)! The section is short and helpful.
|
To discuss next time:
- Be able to crush "Converge or Diverge" questions on demand. We'll spend the entire next class working through and presenting "Converge or Diverge" problems.
- Bonus points if you can highlight a problem (or part of a problem) that you find particularly tricky and explain what we should all be careful of. (You don't even need to be able to solve the problem, but you do need to have thought deeply about why you find it tricky, e.g. what were all the things you tried, and why did they fail.)
|
| Week 11 |
|---|
|
[11.02.15] - Monday Great day of group work and presentations. Every day should be like this.
|
|
Sections covered: 11.7
|
Reading for next time: 11.8. Focus on the following:
- Introduction
|
To discuss next time: Meditate on the fact that "a power series $\sum_{n=0}^\infty c_nx^n$ is a function of $x$."
- Let $\displaystyle f(x) = \sum_{n=0}^\infty x^n$. Writing $f(x)$ out, we get \[f(x) = 1 + x + x^2 + x^3 + x^4 + x^5 +\cdots\]
- Is $f(0.5)$ defined? If so, what is it? How about $f(0)$? $f(1)$?
- Explain why the domain of $f$ is $-1 < x < 1$.
- Explain why $f(x)$ given by the formula $f(x) = \frac{1}{1-x}$ whenever $-1 < x < 1$.
- Let $\displaystyle f(x) = \sum_{n=0}^\infty \frac{x^n}{n!}$. Writing $f(x)$ out, we get \[f(x) = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + \frac{x^5}{120} +\cdots\]
- What do you think is a formula for $f'(x)$? (You do not need to justify your answer!)
- Go to Desmos and graph $\sum_{n=0}^{100} \frac{x^n}{n!}$.
- Based on what you found in the previous part, hazard a guess as to a simpler formula for $f(x)$.
|
|
[11.04.15] - Wednesday
|
|
Sections covered: 11.8 (started)
|
Reading for next time: 11.9. Focus on the following:
- Theorem 2 on page 754 and Notes 1, 2, and 3 that follow it.
- Examples 4 and 5
|
To discuss next time: Consider the function $\displaystyle f(x) = \sum_{n=0}^\infty (-1)^n \frac{x^{2n}}{(2n)!}$. Writing $f(x)$ out, we get \[f(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} - \frac{x^{10}}{10!} + \cdots\]
- Find an expression for $f'(x)$.
- Show that $f''(x) = -f(x)$.
- Find $f(0)$ and $f'(0)$.
- Meditate, and hazard a guess as to a simpler formula for $f(x)$.
- Go to Desmos and graph $\sum_{n=0}^{25} (-1)^n \frac{x^{2n}}{(2n)!}$. Was your guess right?
|
|
[11.06.15] - Friday
|
|
Sections covered: 11.8 (finished), 11.9 (started)
|
Reading for next time: 11.9. Focus on the following:
- Examples 5, 6, and 7
|
To discuss next time: Let's see what can we deduce from the geometric series \[\frac{1}{1-x} = \sum_{n=0}^\infty x^n,\quad\quad -1< x < 1 \]
- Use the geometric series above and ideas from 11.9 to fill in the following blanks.
- $\displaystyle \underline{\hspace{1in}} = \sum_{n=1}^\infty nx^{n-1},\quad\quad -1< x < 1$
- $\displaystyle \underline{\hspace{1in}} = \sum_{n=1}^\infty nx^{n},\quad\quad -1< x < 1$
- $\displaystyle \underline{\hspace{1in}} = \sum_{n=1}^\infty \frac{n}{2^{n}}$
- Explain: \[ \ln 2 = \sum_{n=0}^\infty \frac{1}{(n+1)2^{n+1}}\]
Hint: this one does not build off of the previous parts. Try going back to the geometric series and doing something clever (but different than before)...
|
| Week 12 |
|---|
|
[11.09.15] - Monday
|
|
Sections covered: 11.9 (finished)
|
Reading for next time: 11.10. Focus on the following:
- Introduction through Example 1
- Table 1 on page 768
|
To discuss next time: we now have the following power series representation of $e^x$ \[e^x = \sum_{n=0}^\infty \frac{x^n}{n!} = 1+ x + \frac{x^2}{2!}+ \frac{x^3}{3!} + \cdots,\quad\quad -\infty< x < \infty \]
- Evaluate $\int xe^x \, dx$ by first finding a power series representation for $xe^x$ and then integrating the terms of the power series.
Hint: you can use the above series for $e^x$ to find a power series for $xe^x$; you do not need to start from scratch.
- Of course you can also evaluate $\int xe^x \, dx$ (without series) by using integration by parts. Do it.
- Which of the previous ways was faster? Which gives (in your opinion) a more useable answer?
- Evaluate $\int e^{x^2} \, dx$ any way you want.
|
|
[11.11.15] - Wednesday
|
|
Sections covered: 11.10 (started)
|
Reading for next time: 11.10. Focus on the following:
- Examples 3-7, 10, 11
|
To discuss next time: suppose the Maclaurin series for a function $f$ is \[\sum_{n=0}^\infty \frac{n+2}{2^n} x^n = 2 + \frac{3}{2}x + x^2 + \frac{5}{8}x^3 +\cdots \]
- What is $f(0)$? How about $f'(0)$? What is an equation for the tangent line to $f$ at $x=0$?
- What is an expression for $f^{(n)}(0)$?
|
|
[11.13.15] - Friday
|
|
Sections covered: 11.10 (finished)
|
Reading for next time: 12.1. Focus on the following:
- Introduction through Example 3
|
To discuss next time:
- In Example 2, you saw that the equation $x^2 + y^2 = 1$ represents a circle in $\mathbb{R}^2$, but in $\mathbb{R}^3$, the equation represents an infinite cylinder centered around the $z$-axis.
- Describe the graph of the equation $y=sin(x)$ in $\mathbb{R}^3$.
- How about the general case; that is, can you describe how to graph an equation $y=f(x)$ in $\mathbb{R}^3$?
- Can you write an equation for an infinite cylinder centered around the $y$-axis?
|
| Week 13 |
|---|
|
[11.16.15] - Monday
|
|
Sections covered: 12.1
|
Reading for next time: None. Start reviewing for the exam, which will cover up through Section 11.10.
Don't forget that there's Homework (written and online) due Tuesday!
|
To discuss next time: Let's start reviewing for the exam. Same directions as before...
- Decide which section was the most challenging for you. Meditate on the following, and be prepared to share your answers (especially those who have not presented yet).
- What is an example of a problem from the section that you found challenging?
- What do you feel are the key parts of this problem that you need to understand better?
- Decide which section was the easiest for you. Meditate on the following, and be prepared to share your answers.
- What is an example of a problem from the section?
- What do you feel are the key parts of this problem that your classmates should be aware of so that it becomes easy for them too?
|
|
[11.18.15] - Wednesday Started reviewing for the exam. Good luck y'all!
|
|
Sections covered: review for Midterm 2
|
Reading for next time: None. Focus on studying.
No Homework due Friday!
|
| Week 14 |
|---|
|
[11.30.15] - Monday
|
|
Sections covered: 12.3 (started)
|
Reading for next time: 12.3. Focus on the following:
- Theorem $\fbox{3}$ and Corollary $\fbox{6}$
- The statement labeled $\fbox{7}$
- The section on projections and Example 6
|
To discuss next time:
- Think geometrically to find a vector that is orthogonal to $\langle 0,0,1\rangle$. How many possible answers are there? Can you describe the possible answers geometrically?
- Use $\fbox{7}$ to explain how to find a vector that is orthogonal to $\langle 2,1,1\rangle$. How many possible answers are there? Can you describe the possible answers geometrically? Hint: assume that $\langle x,y,z\rangle$ is orthogonal to $\langle 2,1,1\rangle$ and use $\fbox{7}$ to find possibilities for $x$, $y$, and $z$.
- Use $\fbox{7}$ to explain how to find a vector that is orthogonal to both $\langle 2,1,1\rangle$ and $\langle 1,-1,0\rangle$. How many possible answers are there? Can you describe the possible answers geometrically?
|
|
[12.02.15] - Wednesday
|
|
Sections covered: 12.3 (finished), 12.4 (started)
|
Reading for next time: 12.4. Focus on the following:
- Theorem $\fbox{8}$, Theorem $\fbox{9}$, and Corollary $\fbox{10}$
- The discussion following Corollary $\fbox{10}$ about area of parallelograms
- Examples 3 and 4
|
To discuss next time: Describing planes
- Consider the points $A(1,0,0)$, $B(0,2,0)$, and $C(0,0,3)$. Plot these three points and draw the plane containing them (there is only one). If you need, you can use GeoGebra.
- Read Example 3 in 12.3, and then find a vector $\mathbf{n}$ that is perpendicular to the plane from the first part.
- Suppose that the point $P(x,y,z)$ is in the plane. What is the relationship between $\mathbf{n}$ and the vector $\overrightarrow{AP}$? Hint: draw a picture. Can you use this to quickly determine if $(1,-1,1)$ is in the plane? What about $(2,0,3)$?
|
|
[12.04.15] - Friday
|
|
Sections covered: 12.4 (finished), 12.5 (started)
|
Reading for next time: 12.5. Focus on the following:
- Equations $\fbox{1}$, $\fbox{2}$, $\fbox{4}$
- Examples 1-3
|
To discuss next time:
- First read Examples 2 and 3. Now, consider the following 2 lines (given parametrically)
\[\begin{align*}L_1:&\quad x=8+3t,\quad y=4-t,\quad z=-3+t\quad\quad-\infty< t < \infty\\ L_2:&\quad x=2+s,\quad y=s,\quad z=6+4s\quad\quad-\infty< s < \infty\end{align*}\]
- Find a direction vector for $L_1$. How many possible answers are there for this? Find a direction vector for $L_2$ too.
- By looking at the direction vectors, can you explain why $L_1$ and $L_2$ are not parallel?
- Can you explain why $L_1$ and $L_2$ do not intersect?
- Does $L_1$ intersect the $xy$-plane? If so, where?
|
| Week 15 |
|---|
|
[12.07.15] - Monday
|
|
Sections covered: 12.5 (finished)
|
Reading for next time: 12.6. Focus on the following:
- Examples 3-5
- Table 1 on page 837
|
To discuss next time: Look over Table 1 on page 837.
- How would you change the equation for an elliptic paraboloid so that it opens along the negative part of $x$-axis and has a vertex at $(1,2,3)$? (Of course you can check you answer with GeoGebra.)
- What must be true of the equation for a hyperboliod of one sheet so that the horizontal traces are circles?
- Consider the following equation where $k$ is a constant: \[\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2} = k\]
What types of surfaces are produced when $k$ is allowed to vary between $-\infty$ and $\infty$? For example, what do you get when $k=1$? $k=4$? $k=-4$? Explain. (If you're stuck, try experimenting with GeoGebra.)
|
|
[12.09.15] - Wednesday
|
|
Sections covered: 12.6
|
Reading for next time: None. Start reviewing for the final exam.
Don't forget that there's Homework (the last one!) due Friday.
|
To discuss next time: Let's start reviewing for the final exam. Focus on the new material. Same directions as before...
- Decide which section was the most challenging for you. Meditate on the following, and be prepared to share your answers (especially those who have not presented yet).
- What is an example of a problem from the section that you found challenging?
- What do you feel are the key parts of this problem that you need to understand better?
- Decide which section was the easiest for you. Meditate on the following, and be prepared to share your answers.
- What is an example of a problem from the section?
- What do you feel are the key parts of this problem that your classmates should be aware of so that it becomes easy for them too?
|