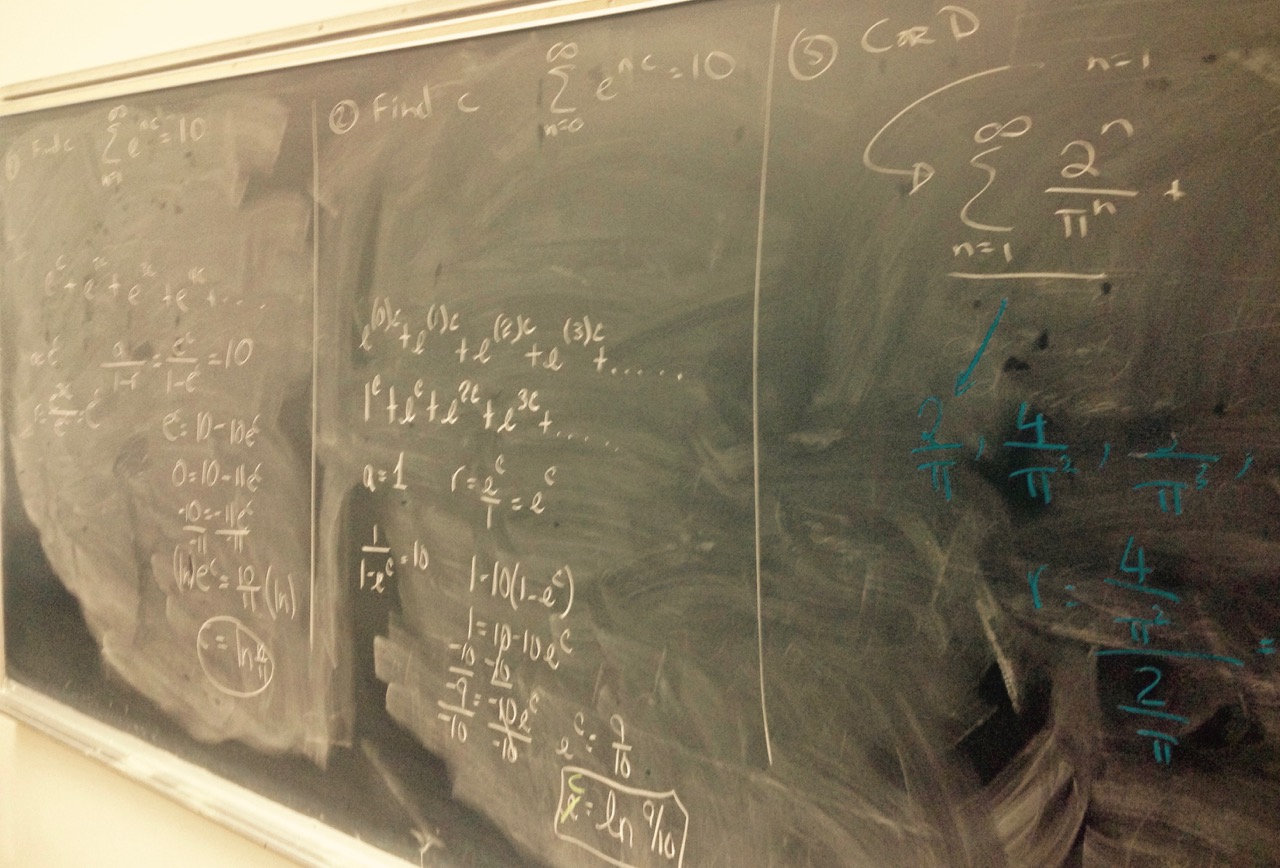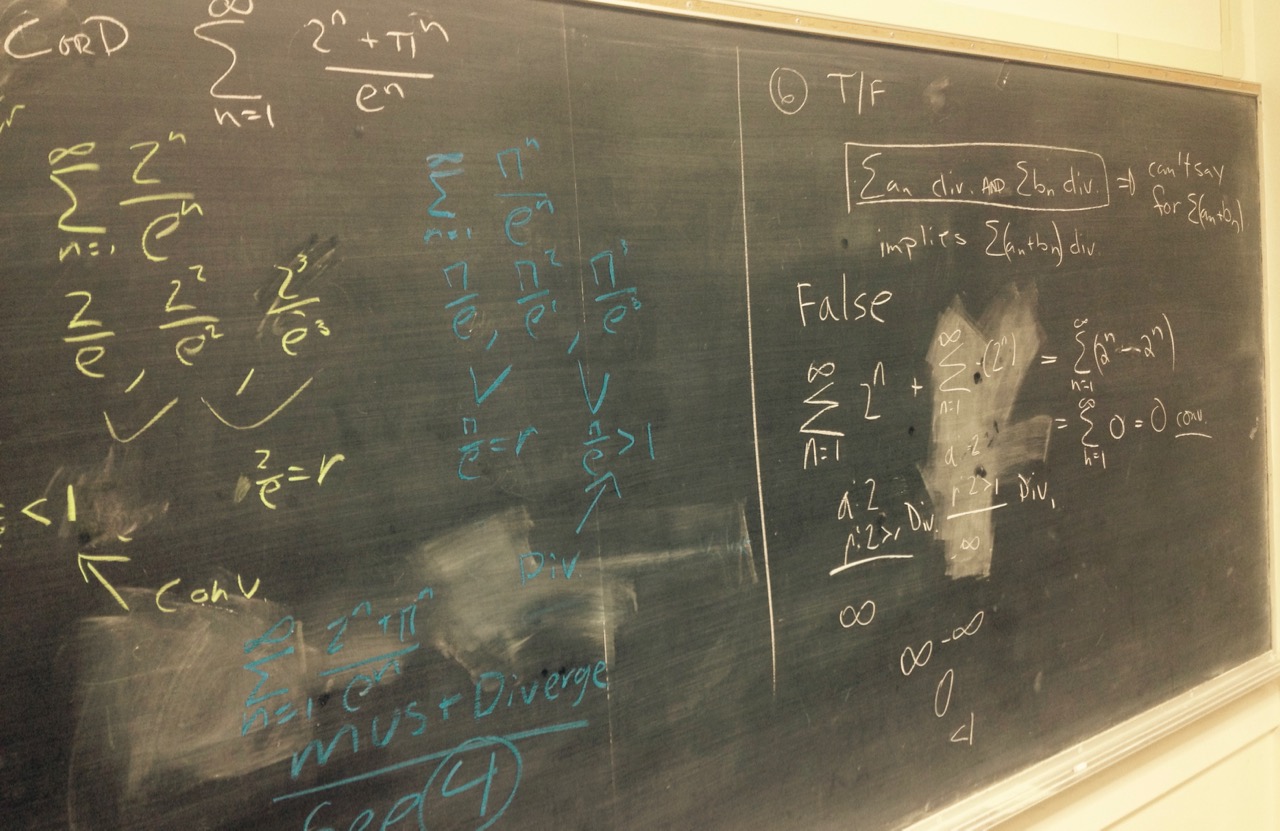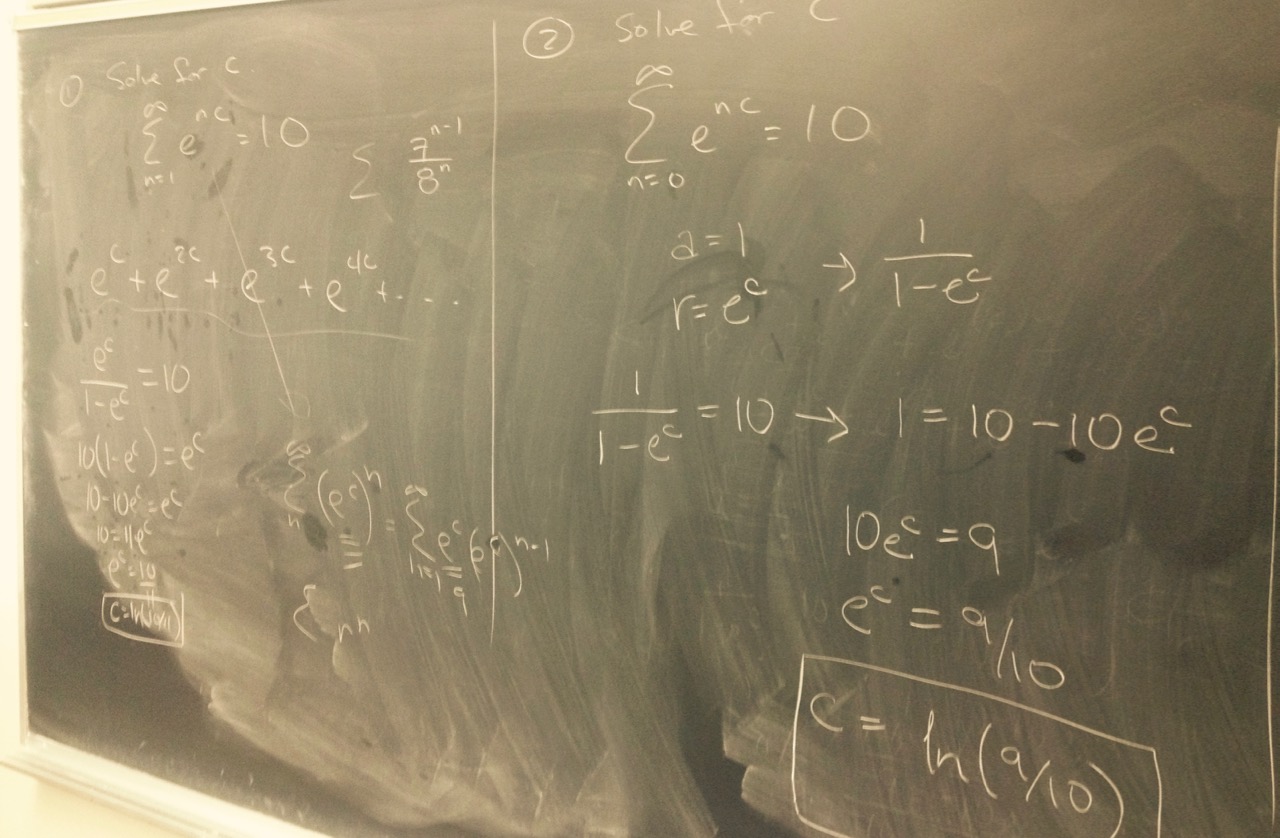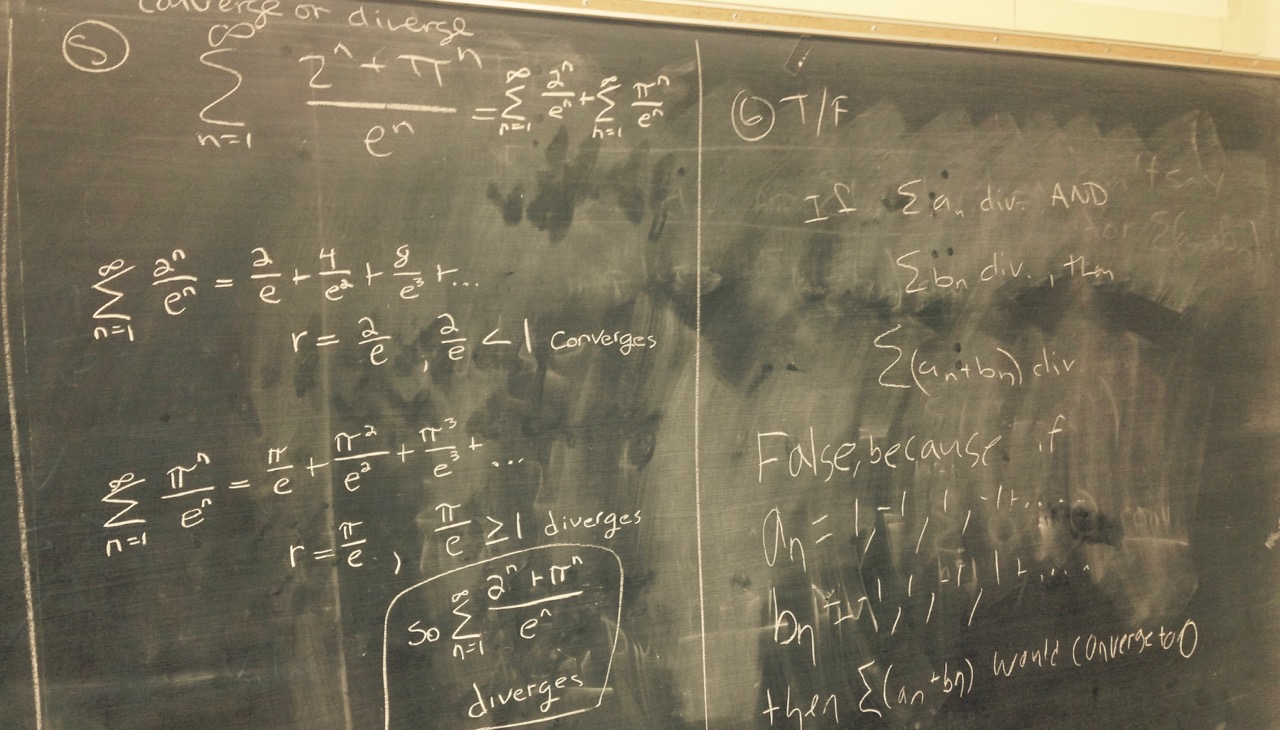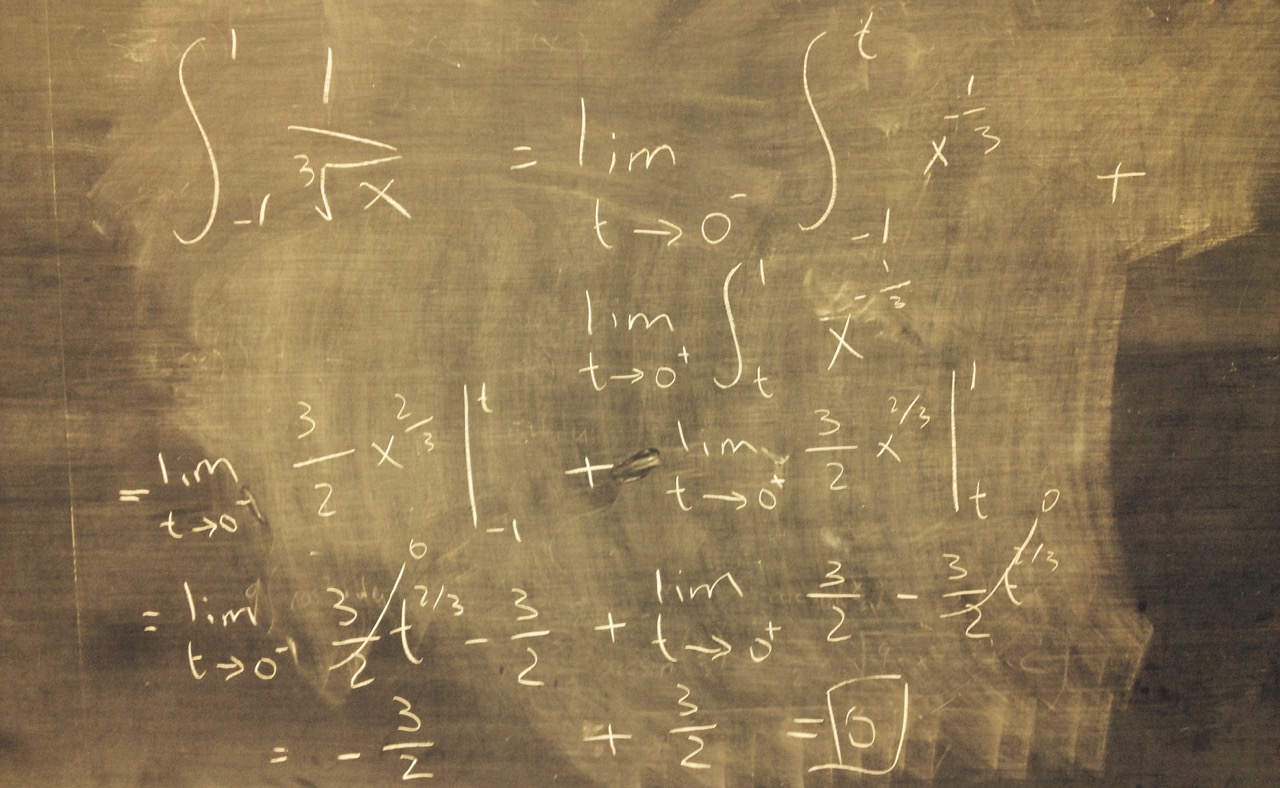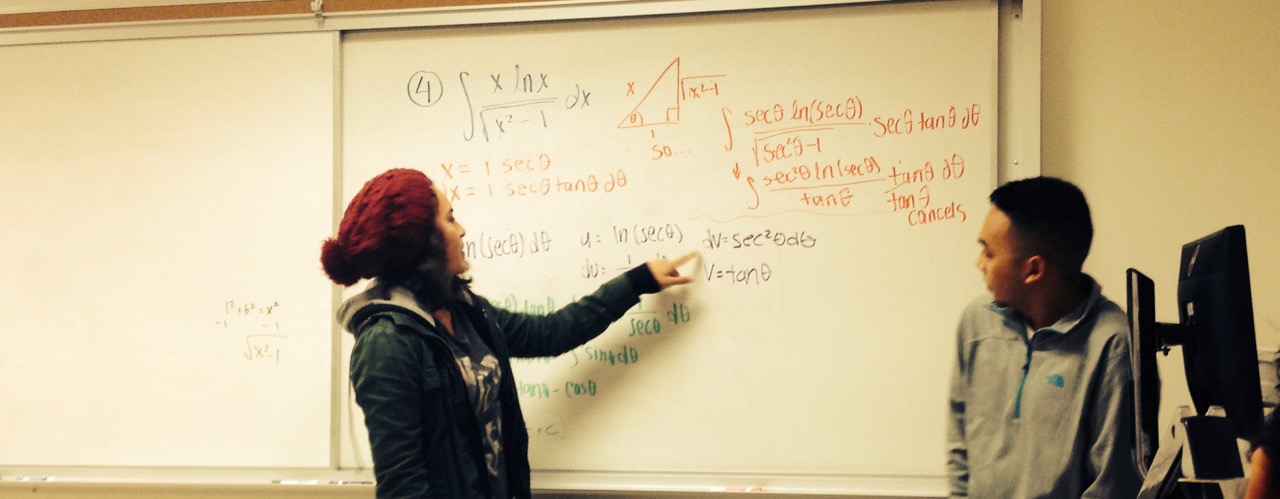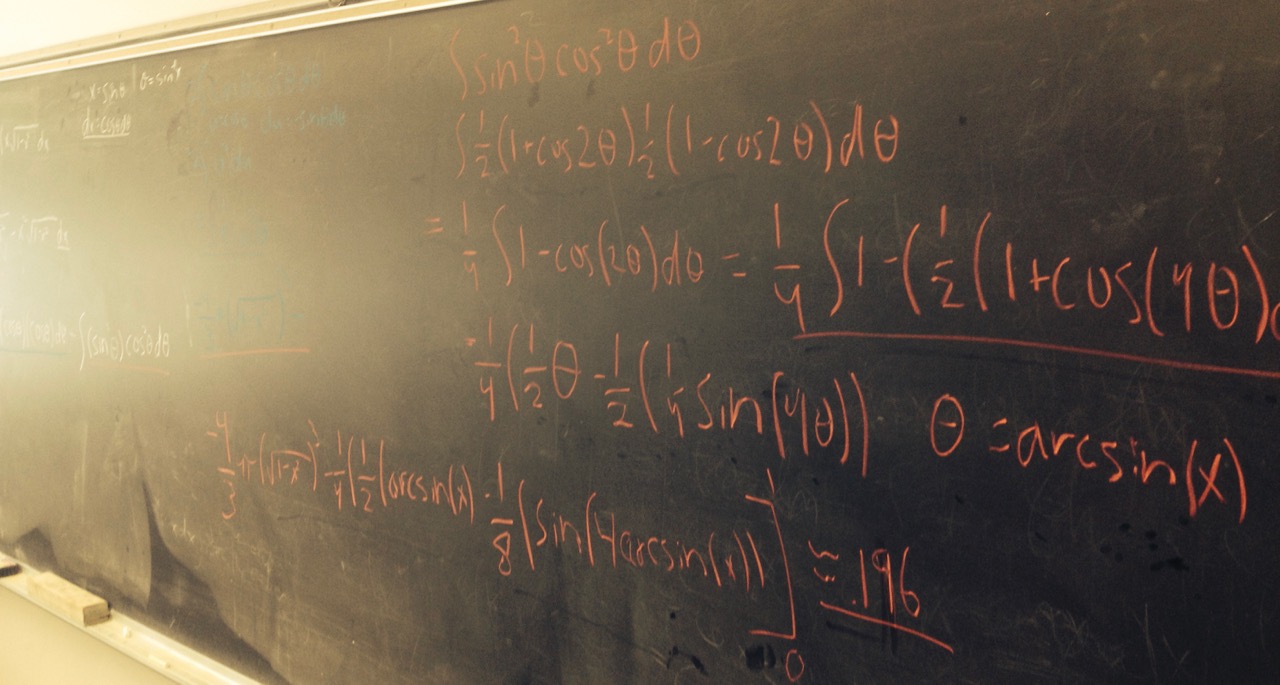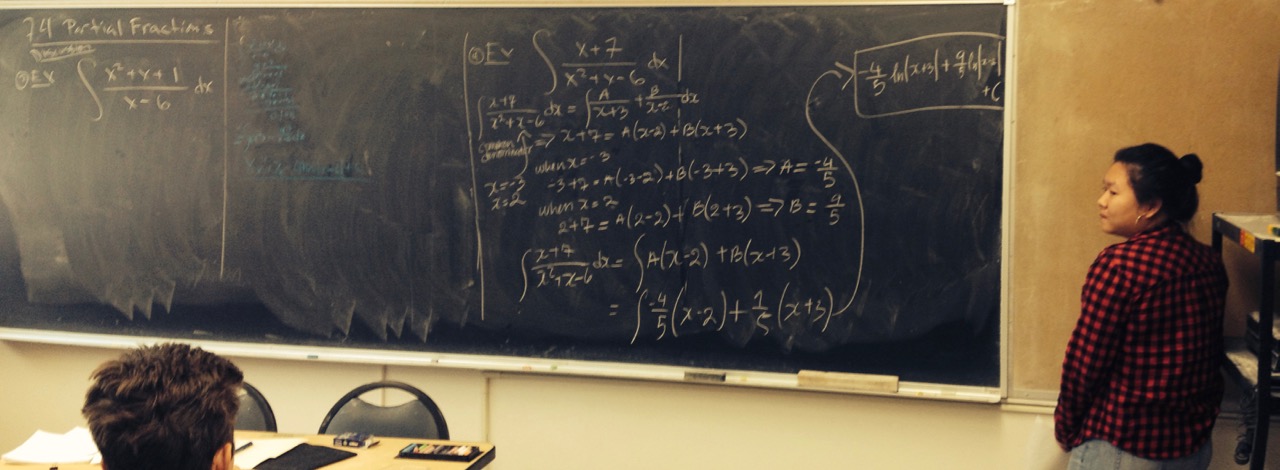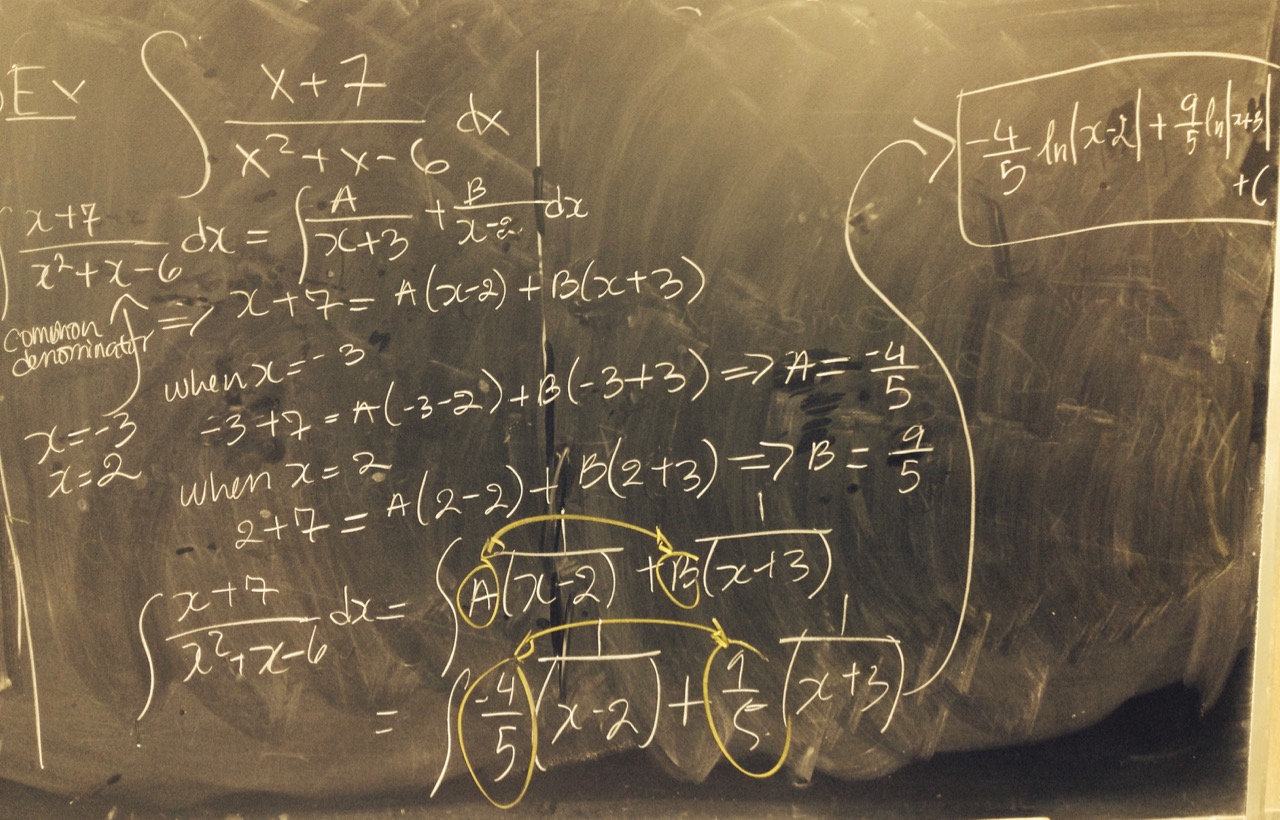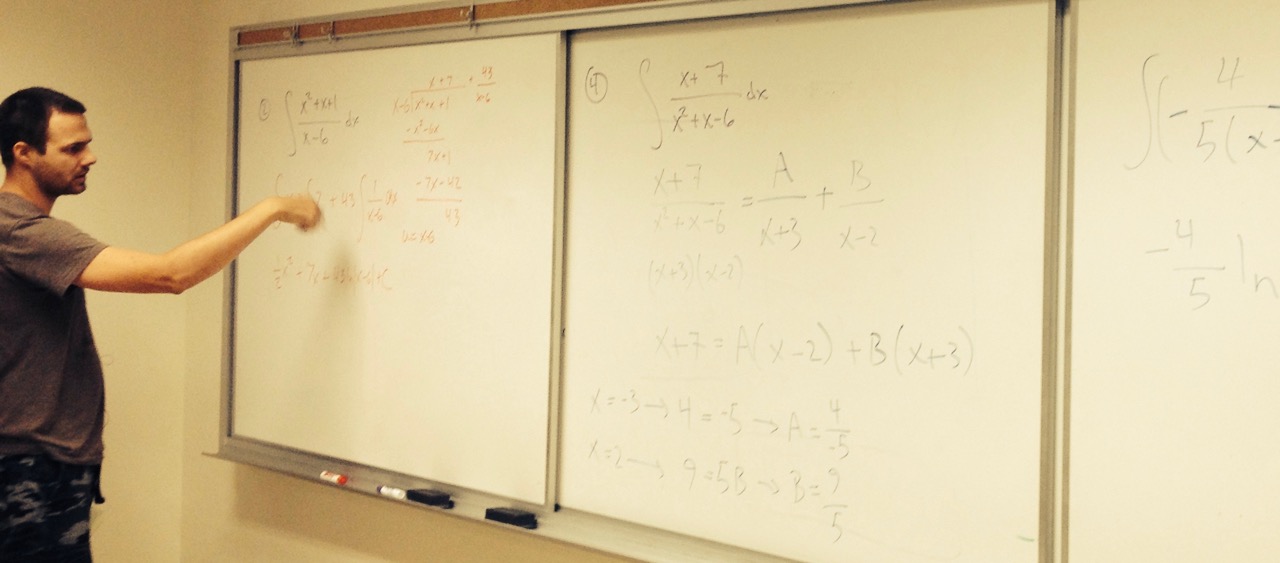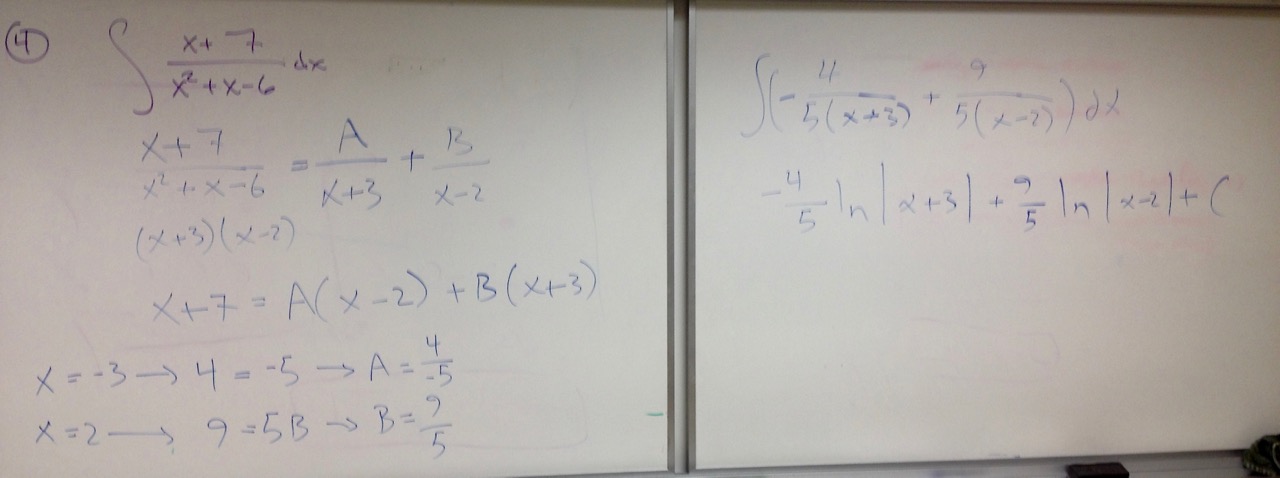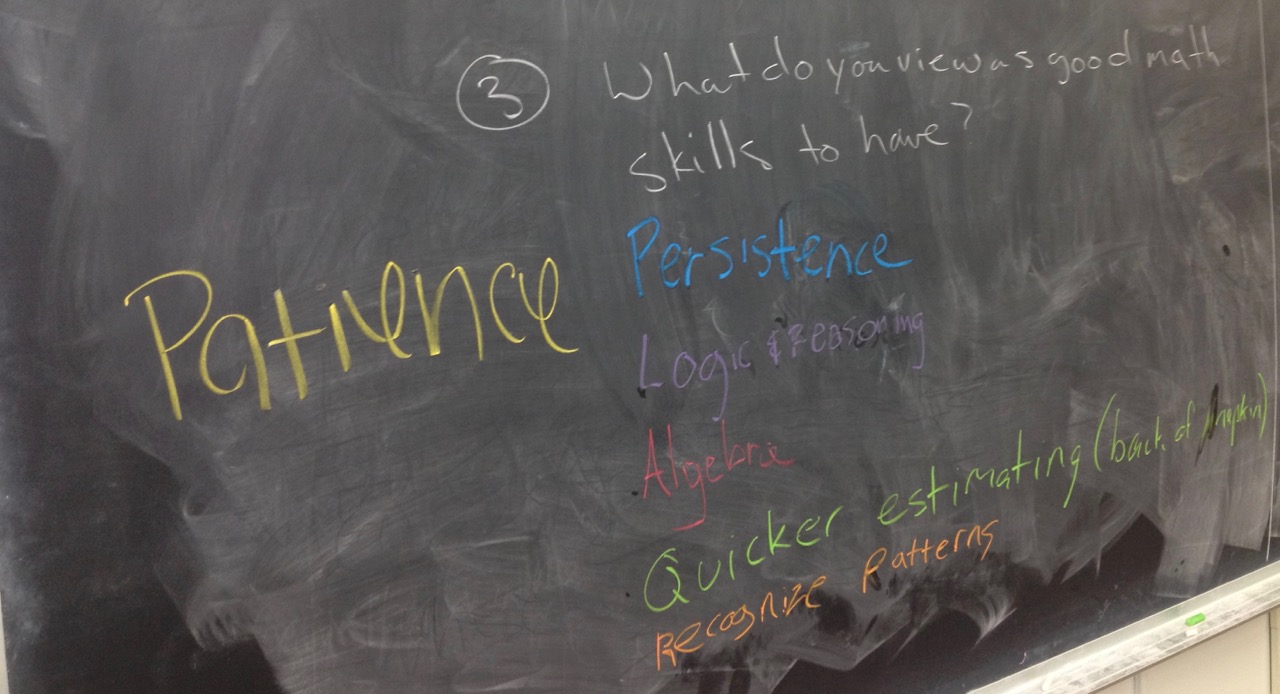Class times for Section 02: 10:00
Class times for Section 04: 12:00
Office Hours: M 11:00
The general course information can be found in the course information handout below. Student grades are maintained on SacCT.
Course Log
| Week 15 |
|---|
|
[12.09.16] - Friday
We did it! Good luck preparing for finals! My office hours next week have been posted in SacCT.
- Miss you already! - |
| Sections covered: Review |
|
[12.08.16] - Thursday
|
| Sections covered: 11.10 (continued) |
| Reading for next time: None. Work on the homework and start reviewing. |
| To discuss next time: Just come prepared for some group work review. |
|
[12.07.16] - Wednesday
|
| Sections covered: 11.9 (finished), 11.10 (started) |
Reading for next time: 11.10. Focus on the following:
|
To discuss next time: the relationship between Taylor series and tangent lines.
|
|
[12.05.16] - Monday
|
| Sections covered: 11.9 (started) |
Reading for next time: 11.9. Focus on the following:
|
To discuss next time: Let's practice building new series from old, via substitution, by trying to find a power series representation for \[f(x) = \frac{2x}{3+x}\]
|
| Week 14 |
|
[12.02.16] - Friday
|
| Sections covered: 11.8 (continued) |
Reading for next time: 11.9. Focus on the following:
|
To discuss next time: Let $\displaystyle f(x) = \sum_{n=0}^\infty (-1)^n \frac{x^{2n}}{(2n)!}$. Writing $f(x)$ out, we get \[f(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} - \frac{x^{10}}{10!} + \cdots\]
|
|
[12.01.16] - Thursday
|
| Sections covered: 11.6 (finished), 11.8 (started) |
Reading for next time: 11.8. Focus on the following:
|
To discuss next time: Let $\displaystyle f(x) = \sum_{n=0}^\infty \frac{x^n}{n!}$. Writing $f(x)$ out, we get \[f(x) = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + \frac{x^5}{120} +\cdots\]
|
|
[11.30.16] - Wednesday
|
| Sections covered: 11.6 (continued) |
Reading for next time:
|
To discuss next time: Meditate on the fact that "a power series $\sum_{n=0}^\infty c_nx^n$ is a function of $x$."
|
|
[11.28.16] - Monday
Back to it. |
| Sections covered: 11.5 (finished), 11.6 (started) |
Reading for next time: 11.6. Focus on the following:
|
To discuss next time: Think about the following questions related to \[\sum_{n=1}^\infty \frac{\sin\left(3^n\right)}{2^n}\]
|
| Week 13 |
|
[11.23.16] - Wednesday
Break time!! |
| Sections covered: Exam |
| Reading for next time: 11.5 + Relax |
| To discuss next time: None. Relax. |
|
[11.21.16] - Monday
Good luck with your studying!! |
| Sections covered: 11.5 (started), Exam Review |
| Reading for next time: None. Study. |
| To discuss next time: None. Study. |
| Week 12 |
|
[11.18.16] - Friday
|
| Sections covered: 11.4 (finished) |
| Reading for next time: Start studying for the exam, but don't forget to check out the questions below. |
To discuss next time: Think about the following questions related to $\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n}$.
|
|
[11.17.16] - Thursday
|
| Sections covered: 11.3 (finished), 11.4 (started) |
Reading for next time: 11.4. Focus on the following:
|
To discuss next time: (carry over from last time) the series $\sum_{n=1}^\infty \frac{1}{n!}$.
|
|
[11.16.16] - Wednesday
|
| Sections covered: 11.3 (started) |
Reading for next time: 11.4. Focus on the following:
|
To discuss next time: the series $\sum_{n=1}^\infty \frac{1}{n!}$.
|
|
[11.14.16] - Monday
|
| Sections covered: 11.2 (finished) |
Reading for next time: (Carry over from last time) 11.3. Focus on the following:
|
To discuss next time: (Carry over from last time)
|
| Week 11 |
|
[11.10.16] - Thursday
Such a good day. Lot's of doing math and tons of excellent presentations!
- So clear! So great! Thanks to all of the presenters! -
|
| Sections covered: 11.2 (continued) |
Reading for next time: 11.3. Focus on the following:
|
To discuss next time:
|
|
[11.09.16] - Wednesday
|
| Sections covered: 11.1 (finished), 11.2 (started) |
Reading for next time: End of 11.2. Focus on the following:
|
To discuss next time:
|
|
[11.07.16] - Monday
Vote!! |
| Sections covered: 11.1 (continued) |
Reading for next time: 11.2. Focus on the following:
|
To discuss next time:
|
| Week 10 |
|
[11.04.16] - Friday
|
| Sections covered: 11.1 (continued) |
Reading for next time: Section 11.1. Focus on the following:
|
To discuss next time: working with factorials. (Make sure to read Example 10 first.)
|
|
[11.03.16] - Thursday
Started sequences and series today - hooray! |
| Sections covered: 10.4 (finished), 11.1 (started) |
Reading for next time: Section 11.1. Focus on the following:
|
| To discuss next time: the worksheet from class today. Keep working through it, and come with questions. |
|
[11.02.16] - Wednesday
Talked about area in polar, and started arc length. On to sequences and series tomorrow. Also, Jullien Gordon will be speaking on campus tomorrow (during the 12pm class ☹). You should definitely consider going if you can. There is more information here: theuniversityunion.com/unique/event/jullien-gordon |
| Sections covered: 10.4 (almost finished) |
Reading for next time: Section 11.1. Focus on the following:
|
| To discuss next time: just come prepared for group work. |
|
[10.31.16] - Monday
Hearts and roses. |
| Sections covered: 10.3 (finished), 10.4 (started) |
Reading for next time: Section 10.4. Focus on the following:
|
To discuss next time: Consider the polar curve $r = 1+2\sin\theta$
|
| Week 9 |
|
[10.28.16] - Friday
Circles and hearts. |
| Sections covered: 10.3 (continued) |
Reading for next time: Section 10.4. Focus on the following:
|
To discuss next time: Repeat from last time: think more about the polar equation $r=\frac{\pi}{\theta}$.
|
|
[10.27.16] - Thursday
On to polar. |
| Sections covered: 10.2 (finished), 10.3 (started) |
Reading for next time: Section 10.3. Focus on the following:
|
To discuss next time: Think more about the polar equation $r=\frac{\pi}{\theta}$.
|
|
[10.26.16] - Wednesday
So happy to get back to the discussions - great day with great presentations! |
| Sections covered: 10.2 (almost finished) |
Reading for next time: Section 10.3. Focus on the following:
|
To discuss next time:
|
|
[10.24.16] - Monday
More calculus with parametric equations |
| Sections covered: 10.2 (continued) |
Reading for next time: Section 10.2. Focus on the following:
|
To discuss next time: Consider the curve $\mathcal{C}$ defined by the parametric equations \[\begin{align*}x=& t^3-3t\\ y=& 3t^2-9\end{align*}\]
This is the same one that was on the last worksheet and was discussed at the beginning of class today.
|
| Week 8 |
|
[10.21.16] - Friday
Group work on parametric equations. |
| Sections covered: 10.2 (started) |
| Reading for next time: None. |
| To discuss next time: None. |
|
[10.20.16] - Thursday
Midterm. |
| Sections covered: Midterm |
| Reading for next time: None. Relax. |
| To discuss next time: None. Relax. |
|
[10.19.16] - Wednesday
Hope you had a good review of integration in class today. I missed you all!
- Asia (over there - across the river) wishes you lots of luck on the exam. And so do I!! - |
| Sections covered: Exam Review |
| Reading for next time: None. Study. |
| To discuss next time: None. Study. |
|
[10.17.16] - Monday
Kept on with the parametric and got started reviewing for the midterm. |
| Sections covered: Section 10.1 (continued) |
| Reading for next time: None. Study. |
| To discuss next time: None. Study. |
| Week 7 |
|
[10.14.16] - Friday
Got a little slowed down by the geometry of cones today ☺, but still had some time to think about different ways of representing a collection of points. There was a nice balance in the class of those that found a function to represent the data (e.g. $y=\sqrt{x} + 1$ or $x = (y-1)^2$) and those that found parametric equations to represent the data (e.g. $(x,y) = (n^2,n+1)$). Nice job everyone! And a special thanks to the one that went to the board; it was super clear, detailed, and, of course, right on! |
| Sections covered: Section 8.2 (finished), Section 10.1 (started) |
|
Reading for next time: (This is a repeat of last time, so if you already did it, focus on studying for the exam.) Section 10.1. Focus on the following:
|
To discuss next time: (This is a repeat of last time, so if you already did it, focus on studying for the exam.)
|
|
[10.13.16] - Thursday
|
| Sections covered: Section 8.2 (continued) |
Reading for next time: Section 10.1. Focus on the following:
|
To discuss next time:
|
|
[10.12.16] - Wednesday
Finished up arc length, and then started surface area by showing that Gabriel's Horn has an infinite surface area (but finite volume)! |
| Sections covered: Section 8.1 (finished), Section 8.2 (started) |
Reading for next time: Section 8.2. Focus on the following:
|
To discuss next time: Revisit the Gabriel's Horn example (included below) from last time, and carefully write out your justification for the comparison test. (Be prepared to share.)
|
|
[10.10.16] - Monday
Arclength today. Many thanks to those who came prepared today and many$^2$ thanks to those that went to the board. |
| Sections covered: Section 8.1 (started) |
Reading for next time: Section 8.2. Focus on the following:
|
To discuss next time:
|
| Week 6 |
|
[10.07.16] - Friday
Finally wrapped up improper integrals. |
| Sections covered: Section 7.8 (finished) |
Reading for next time: Section 8.1. Focus on the following:
|
To discuss next time:
|
|
[10.06.16] - Thursday
Continued making our way through improper integrals. We had several excellent, and highly productive failures in both classes. Many thanks to all those involved!! Unfortunately, I only got a picture of a nonfailure, which nevertheless was also productive ☺
- Crushed. Completely. - |
| Sections covered: Section 7.8 (continued) |
| Reading for next time: Review the solution in the above picture, and note any questions you have. |
| To discuss next time: Nothing new. Study for the quiz. |
| [10.05.16] - Wednesday |
| Sections covered: Section 7.8 (continued) |
Reading for next time: End of Section 7.8. Focus on the following:
|
To discuss next time:
|
|
[10.03.16] - Monday
- Trig. sub. and I.P (and rainbows) - Love it! - |
| Sections covered: Section 7.8 (started) |
Reading for next time: Section 7.8. Focus on the following:
|
| To discuss next time: your feelings about the fact that $\int_1^\infty \frac{1}{x}\,dx$ is infinite while $\int_1^\infty \frac{1}{x^2}\,dx$ is finite. Really, how do you feel? Surprised, happy, sad, lied to, indifferent? |
| Week 5 |
|
[09.30.16] - Friday
Had a fun day of group work with many excellent presentations (though, if you ask me, there were not enough mistakes ☺). Nice job solving hard problems! We'll finish presenting the problems on Monday. Happy Friday!
- "Ugly" integrals and pretty colors - |
| Sections covered: Integration review. |
Reading for next time: Section 7.5. Focus on the following:
|
To discuss next time:
|
|
[09.29.16] - Thursday
More partial fraction decompositions. We'll finally wrap this up tomorrow with you all working through a few more examples. |
| Sections covered: 7.4 (continued). |
| Reading for next time: None. Focus on the homework. |
To discuss next time:
|
|
[09.28.16] - Wednesday
Kept working on partial fraction decompositions. More to come... |
| Sections covered: 7.4 (continued). |
Reading for next time: End of Section 7.4. Focus on the following:
|
To discuss next time:
|
|
[09.26.16] - Monday
Wrapped up trig. substitution today and got started with partial fractions. We had several excellent presentations (but unfortunately ran out of time in both classes)! We'll definitely revisit these at the beginning of Wednesday.
- Slaying partial fractions at 10
- With some small typos corrected - the final answer should also have a swap. (My apologies for rushing the speaker!! I take full responsibility for the typos.) -
- Round 2 at noon -
- Success again! - |
| Sections covered: 7.3 (finished), 7.4 (started). |
Reading for next time: Section 7.4. Focus on the following:
|
To discuss next time: Nothing new, but make sure to review this one from before:
|
| Week 4 |
|
[09.23.16] - Friday
More trig. substitution today. Thanks for all of the help at the board!
- End game. - |
| Sections covered: 7.3 (continued). |
Reading for next time: Section 7.4. Focus on the following:
|
To discuss next time:
|
|
[09.22.16] - Thursday
CarTalked, yet again, today. We had very nice presentations in both classes, and finally, with the help of a lot of trig., found an antiderivative for $\sqrt{100 - x^2}$. |
| Sections covered: 7.3 (started). |
| Reading for next time: None. |
To discuss next time: Try to do the integral that we ended with by following the following steps. (Yes, this one is in the book, but try not to peek.) The integral was \[\int \frac{1}{x^2\sqrt{x^2+4}}\,dx.\]
|
|
[09.21.16] - Wednesday
Exam today. I'll do my best to have it graded quickly. |
| Sections covered: None. |
Reading for next time: Section 7.3. Focus on the following:
|
| To discuss next time: CarTalk! If you remember, the CarTalk problem reduced to solving the following equation for $a$: \[\int_0^a\sqrt{100 - x^2}\,dx = \frac{25\pi}{2}.\] We could estimate this, but we didn't know how to compute it directly because we didn't know an antiderivative for $\sqrt{100 - x^2}$. Use what you read in Section 7.3 to compute $\int \sqrt{100 - x^2}\, dx$. |
|
[09.19.16] - Monday
More trig. fun today, and a little review for the first midterm. Good luck with your studying! (Remember that the first midterm will be Wednesday. It'll cover up through section 7.1.) |
| Sections covered: 7.2 (finished) |
| Reading for next time: None. Focus on preparing for the exam. |
To discuss next time: Focus on preparing for the exam.
|
| Week 3 |
|
[09.16.16] - Friday
Had some fun with trig. today. There will be lots more to come! I promise ☺ Remember that the first midterm will be next Wednesday. It will cover up through section 7.1. |
| Sections covered: 7.1 and the beginning of 7.2 |
Reading for next time: Section 7.2. Focus on the following:
|
To discuss next time: Let's start reviewing for the exam. Meditate on the following questions, and be prepared to share your answers (especially those who have not presented yet).
|
|
[09.15.16] - Thursday
|
| Sections covered: 7.1 (finished, mostly) |
| Reading for next time: None. Focus on studying for the quiz. |
| To discuss next time: Focus on studying for the quiz. In other words, focus on understanding (not just finishing) the written homework for tomorrow. |
|
[09.14.16] - Wednesday
|
| Sections covered: 7.1 (started) |
Reading for next time: Section 7.1 continued. Focus on the following:
|
| To discuss next time: Meditate (again) on the discussion question from last time about the volume of the solid obtained by revolving the region bounded by $y=e^x$, $y=0$, $x=0$, and $x=1$ about the $y$-axis. Remember what the integral looked like if you use washers instead of shells? You have to integrate $(\ln(x))^2$. Can you? That is, be ready to discuss how to compute $\int (\ln(x))^2 \,dx$. Make sure you come prepared to talk about what you tried even if you can't finish the problem. |
|
[09.12.16] - Monday
|
| Sections covered: 6.3 |
Reading for next time: Section 7.1. Focus on the following:
|
| To discuss next time: Finish the example started at the end of class. Find the volume of the solid obtained by revolving the region bounded by $y=e^x$, $y=0$, $x=0$, and $x=1$ about the $y$-axis. Hint: graph it and decide what seems easier to you: shells or washers. Or maybe they both seem hard. (No need to do it the way I chose.) And now the real hint: you will likely need to use integration by parts to finish things off. |
| Week 2 |
|
[09.09.16] - Friday
Wrapped up volumes by disks/wahers today, and found out that Gabriel's Horn, which has an infinite length, holds a finite volume of $\pi$ |
| Sections covered: 6.2 (finished) |
Reading for next time: Continue 6.3. Focus on the following:
|
| To discuss next time: Nothing formal. |
|
[09.08.16] - Thursday
Talked more about volumes today, but ran out of time for Gabriel's Horn. We'll do it first thing tomorrow. |
| Sections covered: 6.2 (almost finished) |
Reading for next time: Finish 6.2 and start 6.3. Focus on the following:
|
| To discuss next time: Can you find the volume of Gabriel's Horn? Gabriel's Horn is the solid obtained by revolving the graph of $y=\frac{1}{x}$, from $x=1$ to $\infty$, about the $x$-axis. Hint: first find the volume of the horn from $x=1$ to $x=a$, and then take the limit as $a\rightarrow \infty$. Be prepared to present a picture and explain the the integral that you came up with, as well as the limit. |
|
[09.07.16] - Wednesday
Dissected eggplants today in the name of Mathematics and found their volumes to (approximately be 288.7cm$^3$ and 249.52cm$^3$. Many thanks to all of those who participated!
- And now we know. - |
| Sections covered: 6.2 (started) |
Reading for next time: More of 6.2. Focus on the following:
|
| To discuss next time: Can you find the volume of Gabriel's Horn? Gabriel's Horn is the solid obtained by revolving the graph of $y=\frac{1}{x}$, from $x=1$ to $\infty$, about the $x$-axis. Hint: first find the volume of the horn from $x=1$ to $x=a$, and then take the limit as $a\rightarrow \infty$. Be prepared to present a picture and explain the the integral that you came up with, as well as the limit. |
| Week 1 |
|
[09.02.16] - Friday
Talked (mostly me ☹)a bit more about areas today, and had a couple of brave souls in both sections share their work with the class. All were great and most came with a touch of productive failure, which I love! Bonus Points! |
| Sections covered: 6.1 (almost finished) |
Reading for next time: Section 6.2. Focus on the following:
|
| To discuss next time: Given a ruler, a calulator, and a knife, can you find a good estimate of the volume of a zucchini? Be prepared to demonstrate. |
|
[09.01.16] - Thursday
Wrapped up our review of Section 5.2 today, as well as the CarTalk problem, for now. But we (and Rich) are still waiting for an actual estimate...anyone? |
| Sections covered: Section 5.2 (finished) |
| Reading for next time: Nothing new. Focus on cleaning up your homework for tomorrow. That is, even if you "got the answers," make sure that everything is written up cleanly and is fully justified. Of course, you can always read more of 6.1 or get into 6.2. |
| To discuss next time: Again, just focus on the homework this time. |
|
[08.31.16] - Wednesday
I really enjoyed the CarTalking today! Thanks to everyone, especially those who presented their ideas at the board and those who commented from the audience. I'm looking forward to hearing from even more of you tomorrow! |
Reading for next time: Section 6.1. Focus on the following:
|
| To discuss next time: CarTalk again: where should Rich from the CarTalk Problem mark for 3/4 of a tank of gas? Focus on trying to reformulate the problem in terms of a definite integral and, of course, try to "solve" the problem, i.e. make as good of an estimate as you can as to where the 20 inch stick should be marked for 3/4 of a tank of gas. |
|
[08.29.16] - Monday - First day!
It was great to meet you all today. Thanks for all of the participation! (But a few of you still owe me a spirit animal...) See you Wednesday!
- Math Skills. - |
Reading for next time: Section 5.2 (and 5.1 if you need to fill in). You should have covered this in Calc 1, but it is very important to review it. Focus on the following:
|
| To discuss next time: Where should Rich from the CarTalk Problem mark for 3/4 tank of gas? Hint: this is hard! The CarTalk clip can be found in the "Content" section of SacCT. Focus on drawing an accurate, and well-labeled picture for the problem. It is totally fine if you don't solve it, but make sure you can clearly explain your approach and where you got stuck. Make sure to indicate if you used outside resources for parts of your solution, e.g. Desmos or WolframAlpha. |