As we get started on Sections 3.1 and 3.2, we’ll focus on cosets, Lagrange’s Theorem, and normality. Lots more on quotients next time.
Results to know
Please read over these problems. You can use these results in future problems even though you are not being asked to prove them.
- Section 3.1: 4, 5, 23
- Section 3.2: 11
Problems to try
Please try to solve these problems, but you do not turn them in. You can also use these results in future problems. I’m happy to talk about these problems (or any others) if you have questions.
- Section 2.5: 4
- Section 3.1: 1, 28, 29, 38, 40, 41
- For #41, both of #28 and #40 should be helpful.
- Section 3.2: 5, 8, 16
- For #5, it might be helpful to use one of the additional problems below.
- Additional Problem. Let $G$ be a group. Prove that a group is finite if and only if its subgroup lattice is finite.
- For the reverse direction, think about cyclic subgroups.
- Additional Problem. Let $G$ be a group. Prove that for all $g\in G$ the map $\gamma_g: G \rightarrow G$ defined by $\gamma_g(a) = gag^{-1}$ is an automorphism of $G$.
Problems to submit
These are the problems to turn in for a grade. Please write in complete sentences, use correct punctuation, and organize your work. Once your finish these problems, please follow the directions in the Canvas assignment to submit them. If you have any questions (about the math or writing or submission process or anything), please let me know!
-
Section 3.1: 24
-
Section 3.1: 42
-
Section 3.2: 16
-
Additional Problem. Prove that the lattice below can not be the subgroup lattice of any group.
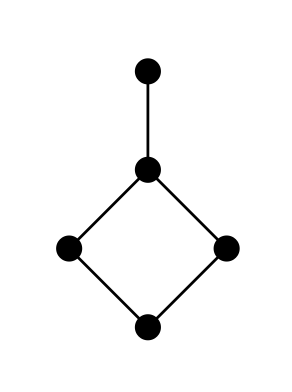
Comments: Suppose the subgroup lattice of some group $G$ is isomorphic to this lattice. It’ll probably help to label each node with a letter representing a subgroup. (Of course, you know what the top and bottom subgroups are.) You may want to think about elements of $G$. If some subgroup $H$ does not contain an element $a$, then where might $\langle a \rangle$ be in the picture?
