Course Information
Books & Resources
Material will be selected from various texts. Likely sources include the following:
- Groups: An Introduction to Ideas and Methods of the Theory of Groups, by Antonio Machì
- Notes on Group Theory, by Mark Reeder
- Simplicity of $\operatorname{PSL}_n(F)$, by Keith Conrad
- Notes on Classical Groups, by Peter J. Cameron
- Notes on Finite Group Theory, by Peter J. Cameron
- Finite Group Theory, by I. Martin Isaacs [Available in my library]
- A Course in the Theory of Groups by Derek Robinson [Available in my library]
Tentative List of Topics
A tentative list of what we will cover is below, but be aware that it is subject to change.
- Advanced permutation group theory
- Possible topics: primitivity, multiple transitivity, Iwasawa’s lemma
- Simplicity of $\operatorname{Alt}(n)$ and $\operatorname{PSL}(n,F)$
- Advanced Sylow Theory
- Transfer Theory and Burnside’s Normal $p$-complement Theorem
- Application: classifying the simple groups of order at most 200
- Additional topics (time permitting)
- Possible topics: characterizations of finite nilpotent groups, group extensions and group cohomology
Problem Sets
Course Log
Week 15
What we covered: Took stock of our work and tidied up some loose ends to see that we have established the classification of the simple groups up to order 200, except for order 168. We then quickly discussed groups of the form $\operatorname{PSL}_2(F)$, and computed orders to see that $\operatorname{PSL}_2(\mathbb{F}_7)$ is an example of a simple group of order 168. We ended by roughly outlining an approach to show that this is in fact the only simple group of order 168 (up to isomorphism). Thanks for a fun semester you all!
Photos from the day
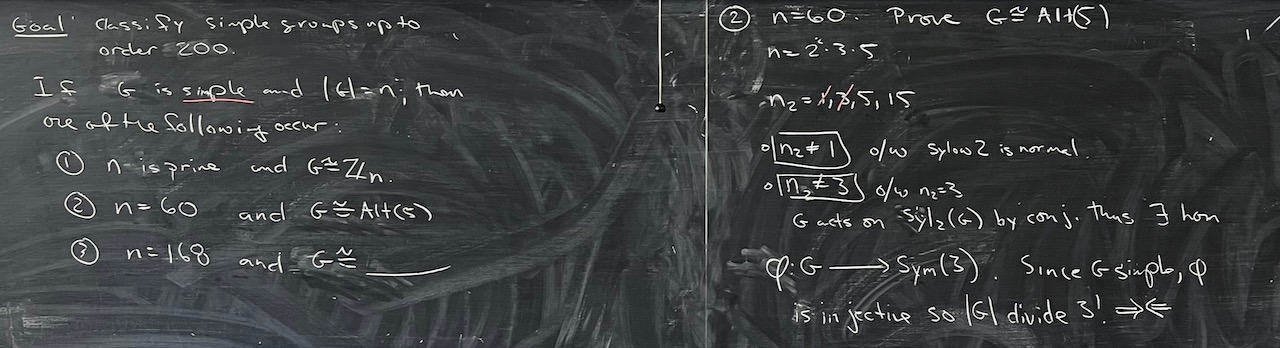 |
 |
 |
 |
Week 14
–Fall Break–
Week 13
What we covered: Started by taking stock of our work so far and writing out our target theorem. We organized the work that remains, and in doing so, we also briefly introduced the groups $\operatorname{PSL}_n(F)$. We then used the remaining time to analyze simple groups of order 120, eventually showing that they don’t exist.
To work on for next time: Continue to focus on the remaining orders of groups up to 200 that our results don’t cover (see Problem 7 of Problem Set 05). Try to deal with everything other that 60 and 168; this is the main task. Additionally, try to work on:
- Problem 5 of Problem Set 05
- Look over Problem Set 06 and maybe try Problem 2
- Continue to write/polish/organize the work we’ve already completed
Photos from the day
 |
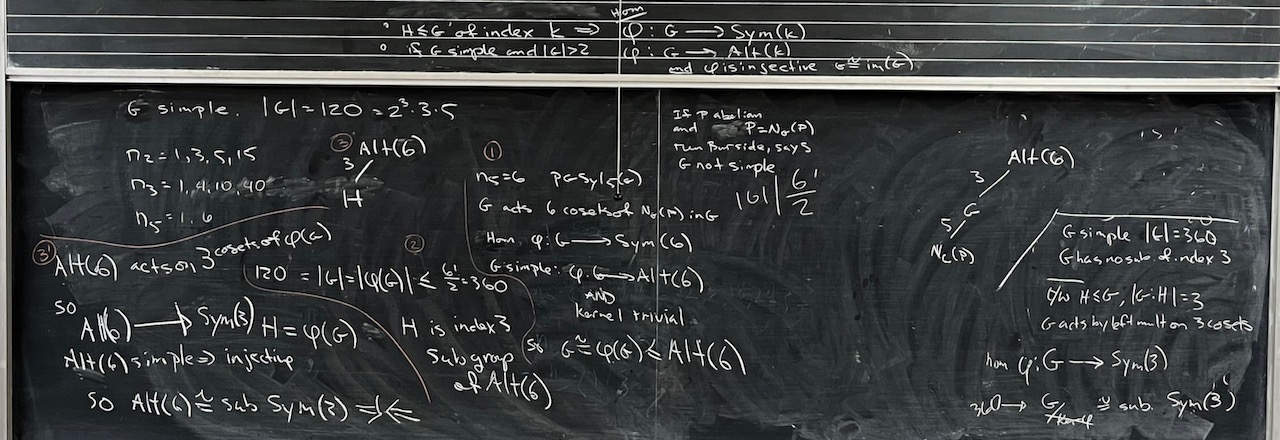 |
Week 12
What we covered: Spent most of our time analyzing groups of order dividing $2^4q^2$ and got a nice proof of their nonsimplicity (except when the group has prime order). In the final minutes we looked at some of the reminaing orders of groups that our results don’t cover. Many fell quickly (like orders 96,108,140), but 120 was more challenging…however, we seem to have a good start. Maybe folks can finish that one for next time…
To work on for next time: Focus on the remaining orders of groups up to 200 that our results don’t cover (see Problem 7 of Problem Set 05). Can you deal with everything other that 60 and 168, or are there some orders that are putting up a good fight? Also try to work on Problem 6 of Problem Set 05 as well as writing/polishing/organizing the work we’ve already completed.
Photos from the day
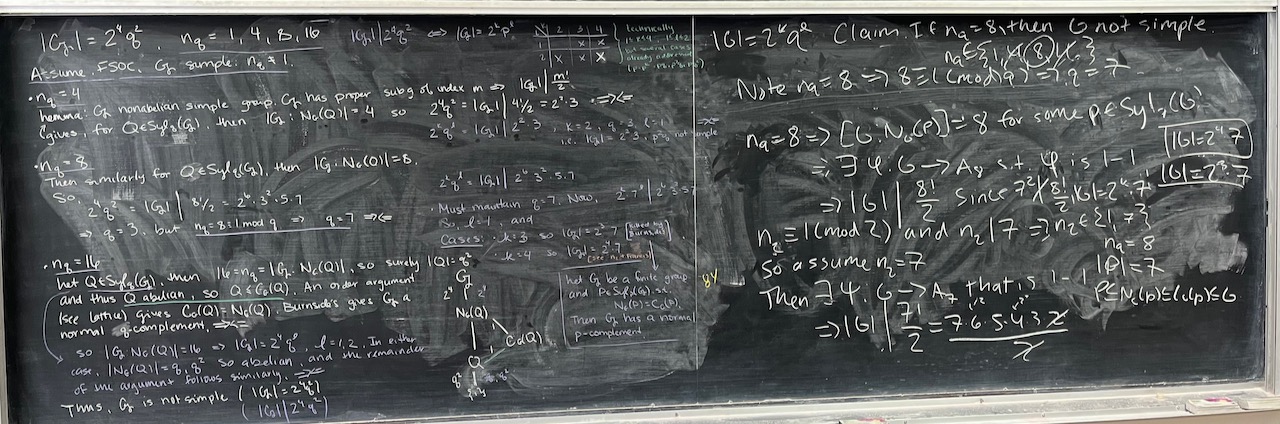 |
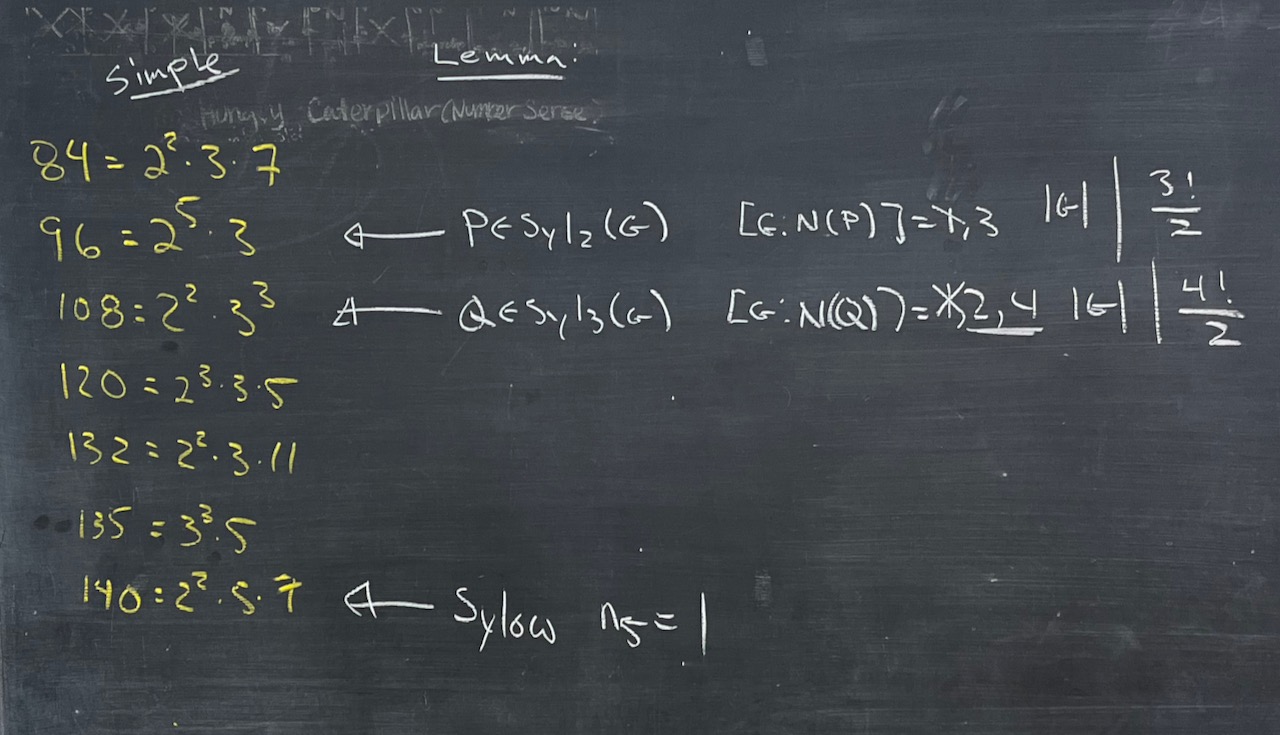  |
Week 11
What we covered: Mostly just an extended checkin following the events of the week. Hope folks are able to find some space to recharge at least a little over the long weekend.
To work on for next time: Same as last time. Some subset of: Problem 3 from Problem Set 04 and all of Problem Set 05
Week 10
What we covered: Talked through the two problems from last time (Problem 1 from Problem Set 04 and Problem 4 from Problem Set 05) and then discussed as a group Problem 2 from Problem Set 04.
To work on for next time: Some subset of: Problem 3 from Problem Set 04 and all of Problem Set 05
Notice that Problem Set 05 has been modified quite a bit: there is a new part to Problem 4 as well as an entirely new problem on the simplicity of the alternating groups.
Week 09
What we covered: Got a couple of good problems on the board today: Problem 1 from Problem Set 04 and Problem 4 from Problem Set 05. We had lots of good conversations in groups but did not talk through things as a group yet. We’ll start there next time.
To work on for next time: Some subset of: Problems 2,3,6 from Problem Set 04 and Problems 1,2,5 from Problem Set 05
Photos from the day
 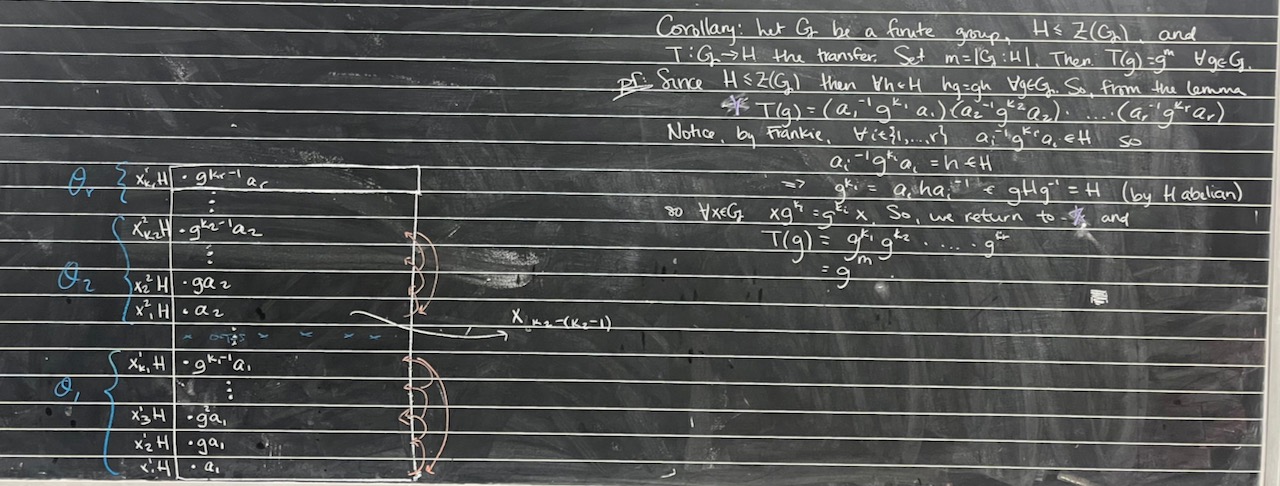 |
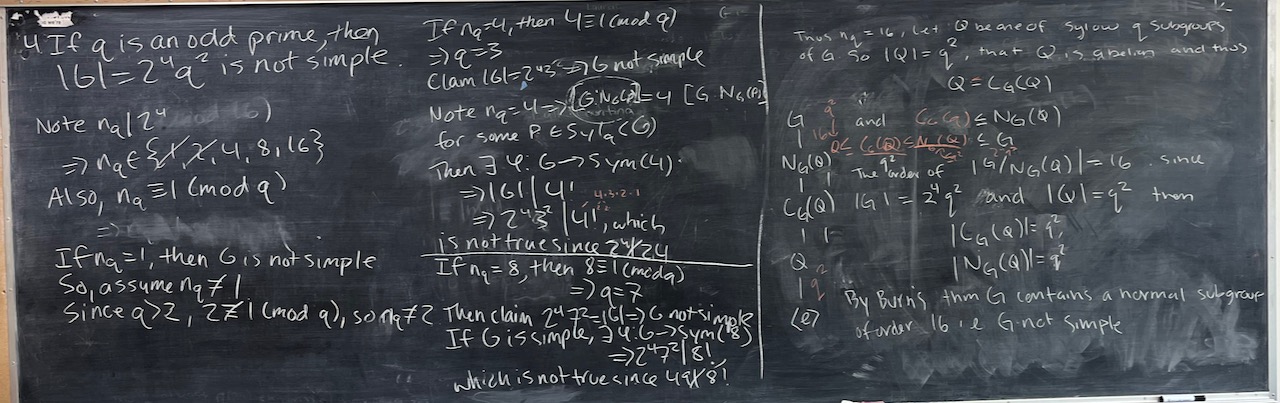 |
Week 08
What we covered: Worked through more of the details about the transfer and got the first key properties up on the board: it is a homomorphism and it does not depend on the choice of transversal, see Problem #2 from Problem Set 03. (Leveraging these, we’ll continue with the transfer evaluation lemma next time and then prove Burnside’s Normal $p$-complement Theorem.) We also worked through a first application of Burnside’s theorem using it to prove that there are not simple groups of order 400 (Problem #4 from Problem Set 04).
To work on for next time: Some subset of: Problems 1,2,3,6 from Problem Set 04 and Problems 4,5 from Problem Set 05
Photos from the day
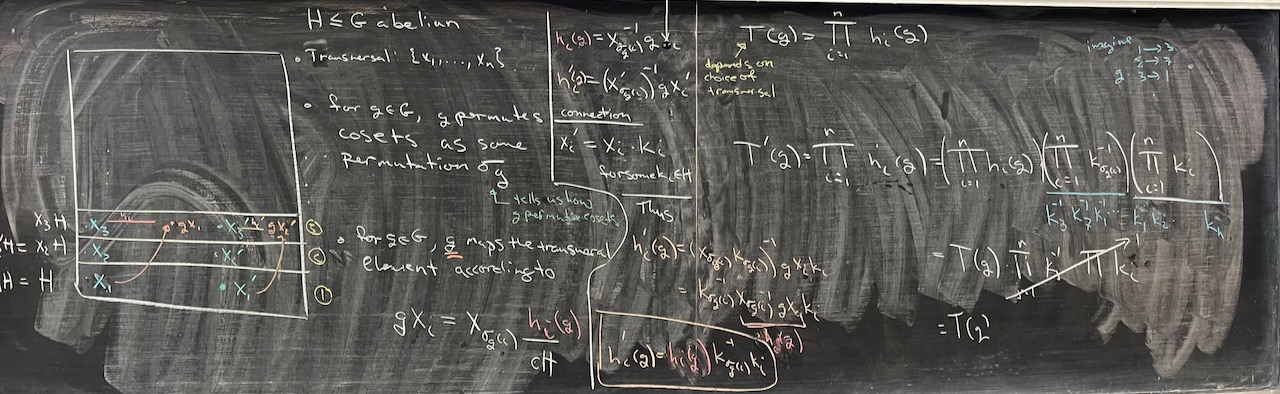 |
  |
Week 07
What we covered: No group meeting this week. We’ll keep working the problems from last time. There were some small adjustments and corrections made to Problem Set 04, so please make sure to use the current version.
To work on for next time: Some subset of: Problems 1,2,3,6 from Problem Set 04.
Week 06
What we covered: Worked on Problem 1 from Problem Set 03 and Problem 5 from Problem Set 04 and then tried to make a little more sense about the transfer map. We’ll prioritize getting through the (highly technical!) “basics” of the transfer next time, and then we can start looking at the payoff.
To work on for next time: Some folks have an exam…right? If so, that is priority number one. After that, see how much of the transfer you can digest: an ambitious target would be Problem 2 from Problem Set 03 and Problems 1 and 2 from Problem Set 04. If the transfer puts up a big fight, then spend some time on Problem 6 from Problem Set 04.
Photos from the day
  |
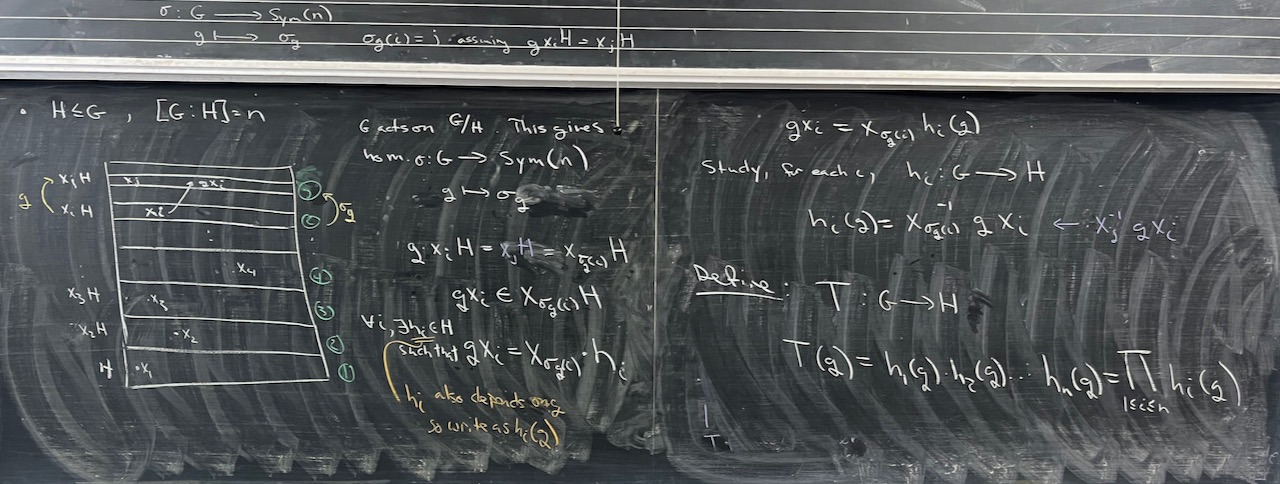 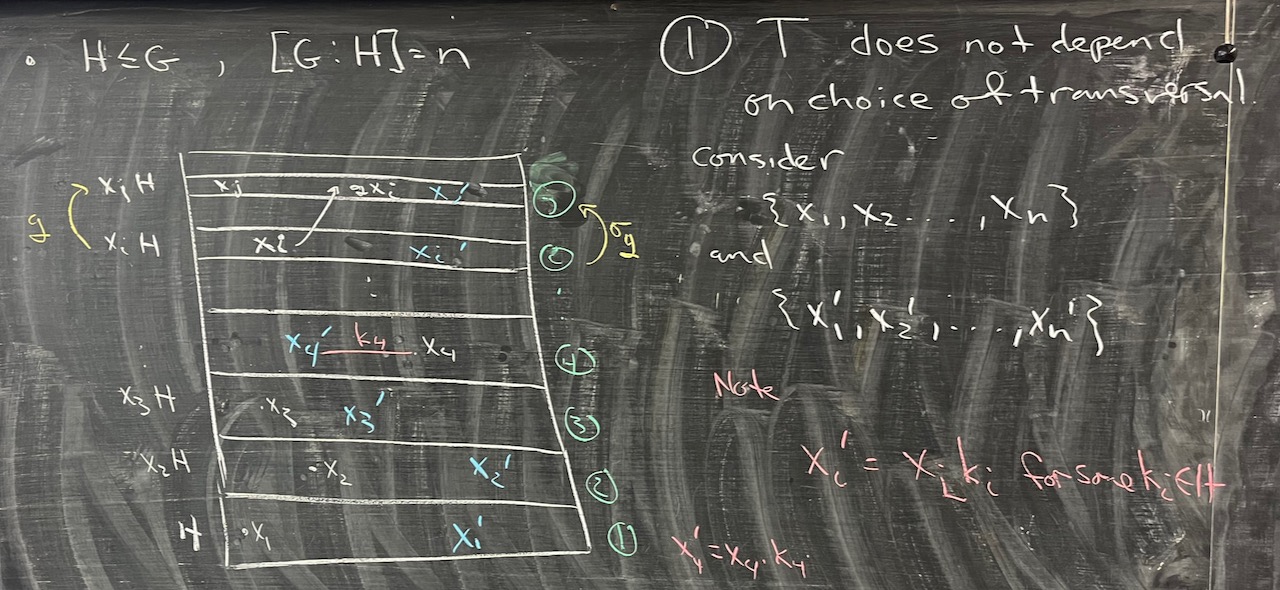 |
Week 05
What we covered: Finished Problem Set 02 today with a proof that a group of order $2m$, with $m$ odd, has a subgroup of index $2$ by looking closely at the left-regular representation. After that we took a look at groups of order 12 showing at they either have a normal Sylow 3-subgroup or they are isomorphic to $\operatorname{Alt}(4)$. With the remaining time, we started making sense of the definition of the transfer map as well as what it means for a group to have a normal $p$-complement. Much more with transfer next time.
To work on for next time: Problems 1 and 2 from Problem Set 03 and Problems 5 and 6 from Problem Set 04. And if you want to go a little further with the transfer this week, try Problem 1 from Problem Set 04.
Photos from the day
 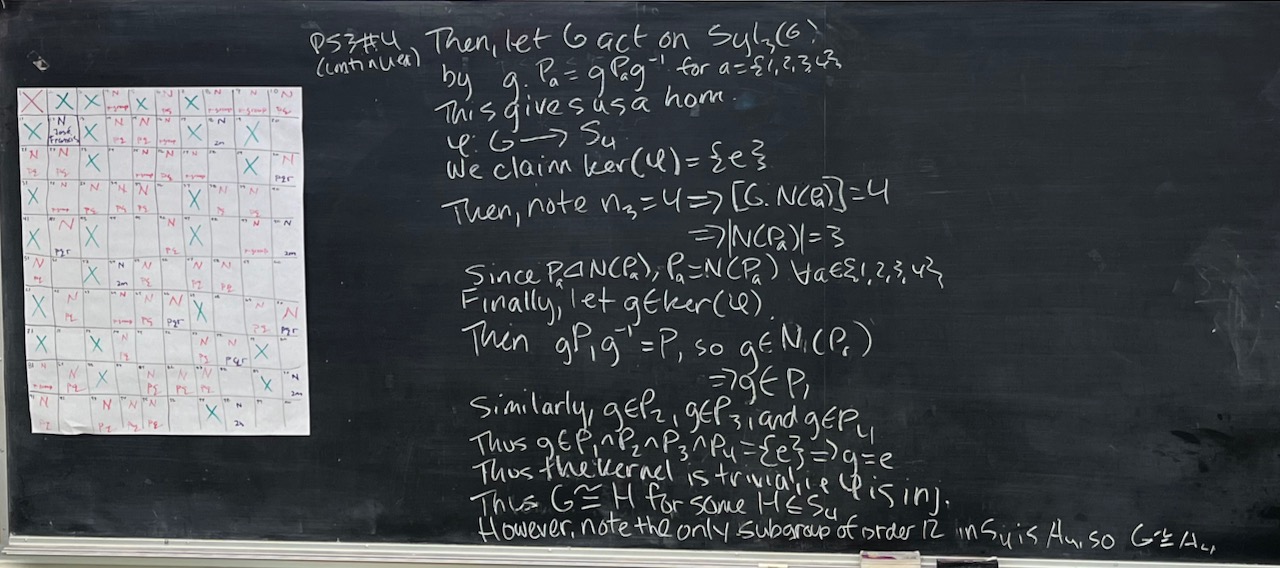 |
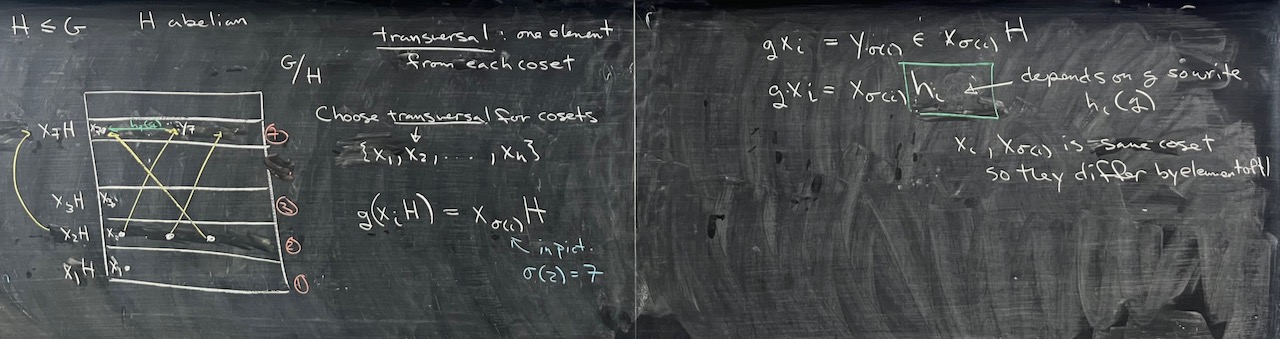 |
Week 04
What we covered: Worked though most of Problem Set 02 today. We started by showing that among all finite abelian groups and all $p$-groups, the only simple ones are those of prime order. Next, we took a look at groups of order $pqr$ (distinct primes) and put together a counting argument to show that no such group is simple. We wrapped up with a result that describes the cycle-structure of elements in the image of the left regular representation. It may seem a little off topic, but next time we’ll apply it develop another non-simplicity test (see #4 in Problem Set 02).
For next time, we’ll keep working on Problem Set 03 (as well as #4 from Problem Set 02).
To work on for next time: Problem Set 03
Photos from the day
 |
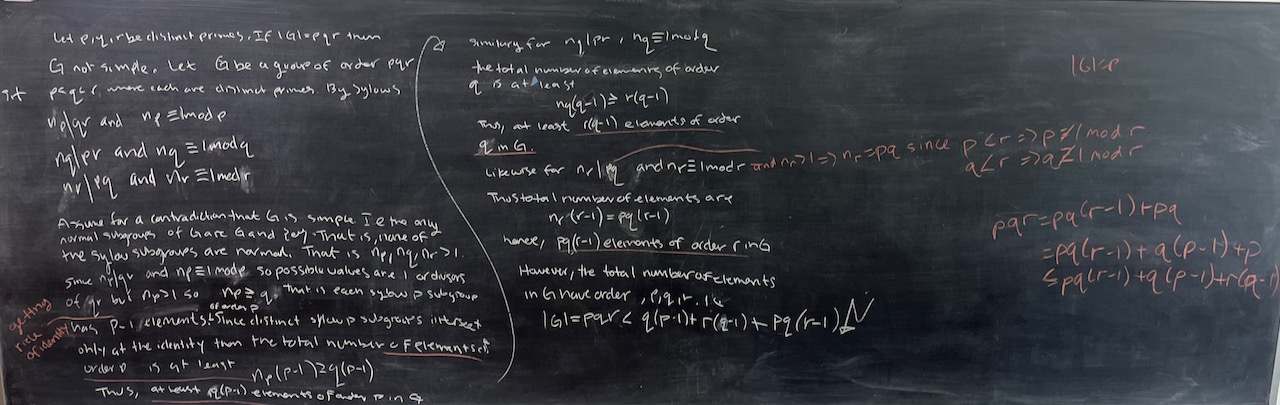 |
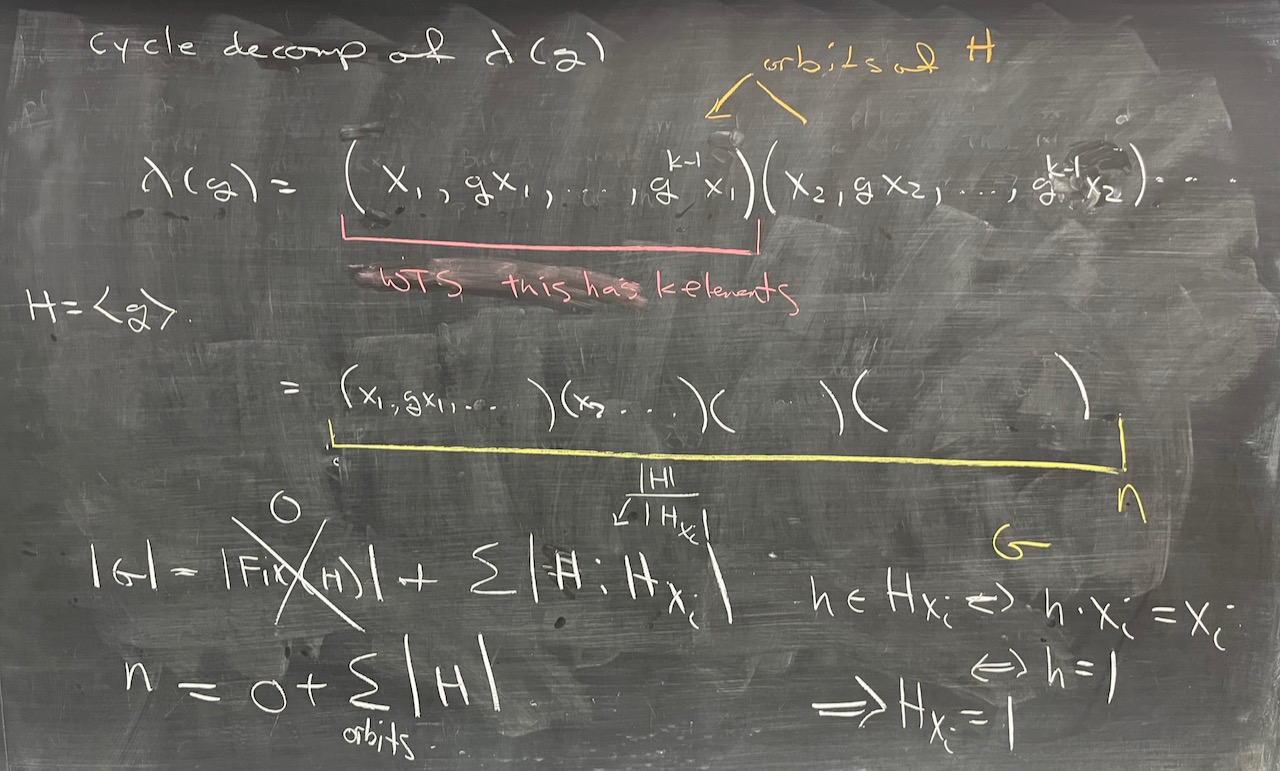 |
Week 03
What we covered: Started by revisiting Problem Set 01 to work through a proof of conjugacy of Sylow subgroups—nice job! After that, we got into Problem Set 02. We discussed the second problem showing that a proper subgroup of a simple group can not be too large. Next we looked at groups of order $pq$ and gathered some ideas about groups of order $pqr$. We’ll return to the remaining problems next time and also start learning about the transfer homomorphism.
To work on for next time: Problem Set 03
Photos from the day
 |
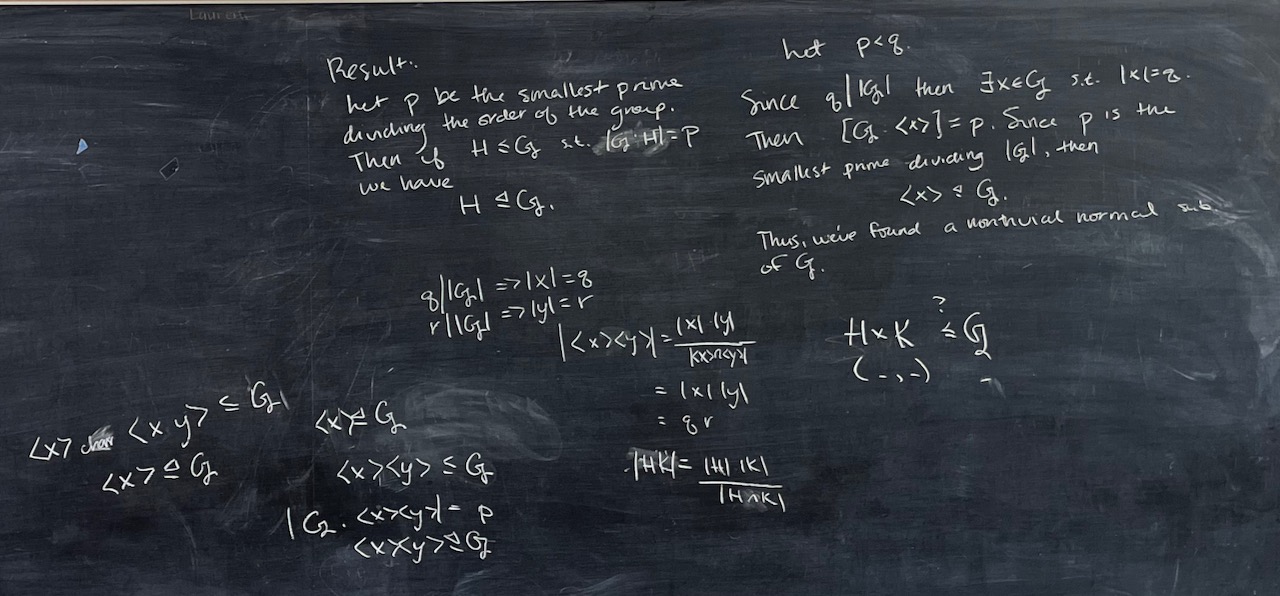 |
Week 02
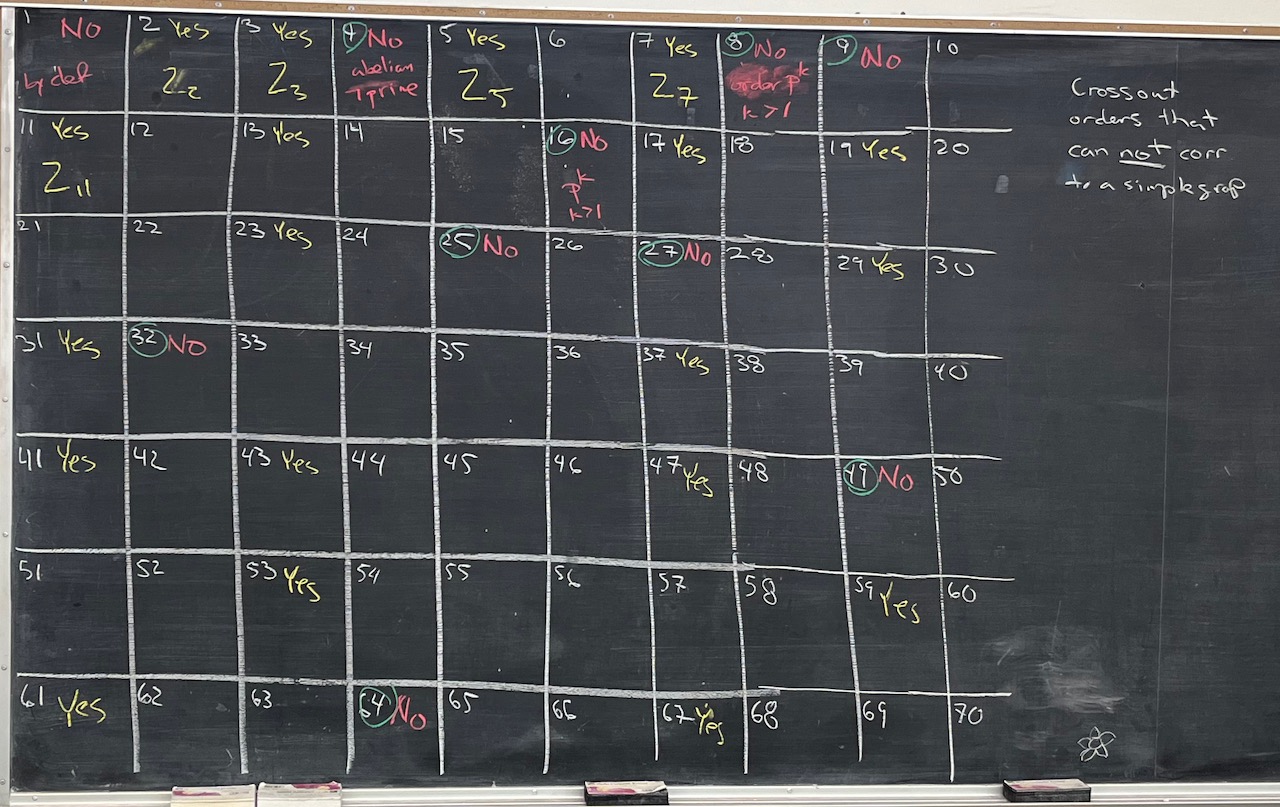
What we covered: We worked through a lot of Problem Set 01 but had to save Sylow for next time. We applied some of what we learned to groups of order up to 70 and saw that we could determine simplicity for all of the prime power orders (but have small details to finalize in the next problem set). In the next weeks, we’ll start bringing Sylow to bear and also develop some other tools. Pictures below. Great day—thank all!
To work on for next time: Problem Set 02
Photos from the day
 |
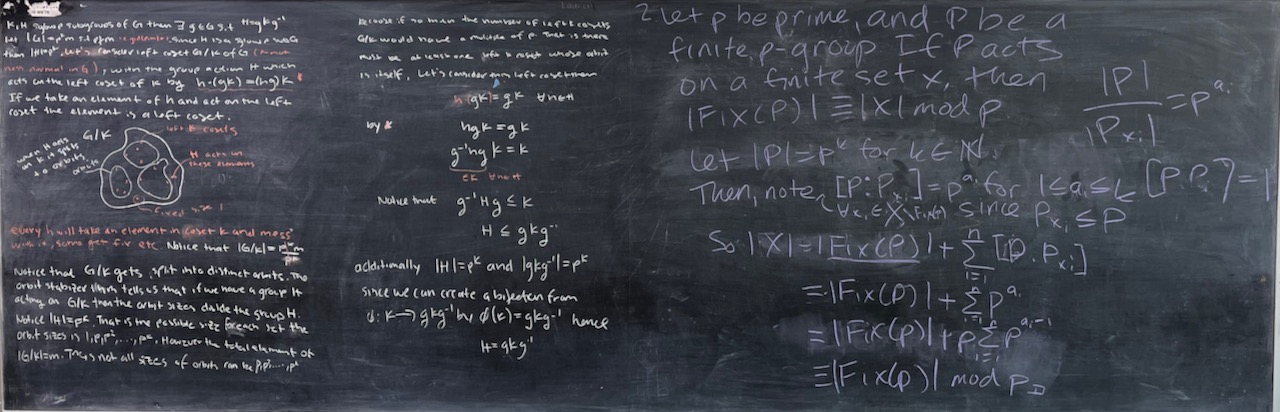 |
 |
Week 01
What we covered: Syllabus, planning, and overview of our work ahead. We ended with a discussion of simple groups, the Hölder program, and the classification of the finite simple groups (CFSG). For a fun and more visually interesting view of CFSG (and the sporadic groups), watch the video below.
To work on for next time: Start working on Problem Set 01
