Course Information
Meeting times
- Section 03: Tues and Thur from 1:30–2:45 PM (SQU 142)
Book(s)
- An Inquiry-Based Approach to Abstract Algebra by D.C. Ernst (the book is free and open source)
Daily Homework
Writing Assignments
Course Log
[05.09.24] - Thursday - Final Class Meeting!
| What we covered: Last class of the semester! Talked through the remaining problems on quotients, homomorphisms, and the First Iso Theorem, and then wrapped up with main task for the day: group photo. Thanks for a great semester everyone! Good luck prepping for the final (you’ve got it!), and look forward to continuing on in the Fall. |
 |
 |
 |
[05.07.24] - Tuesday
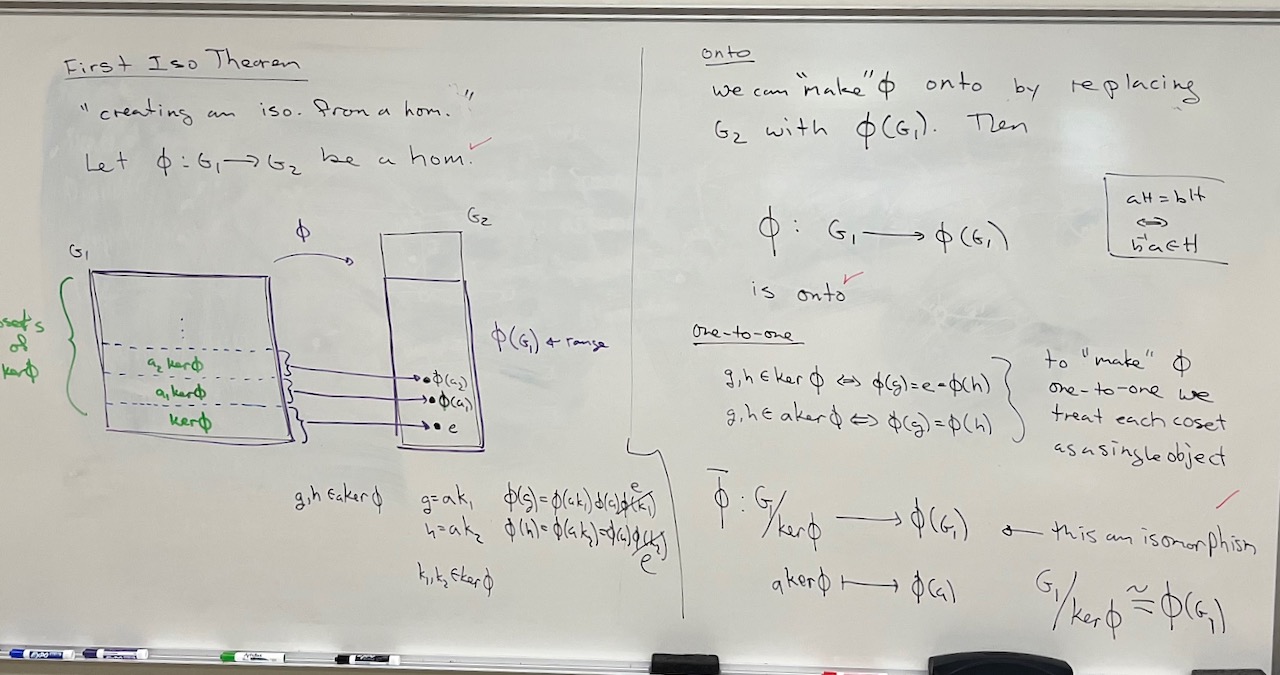
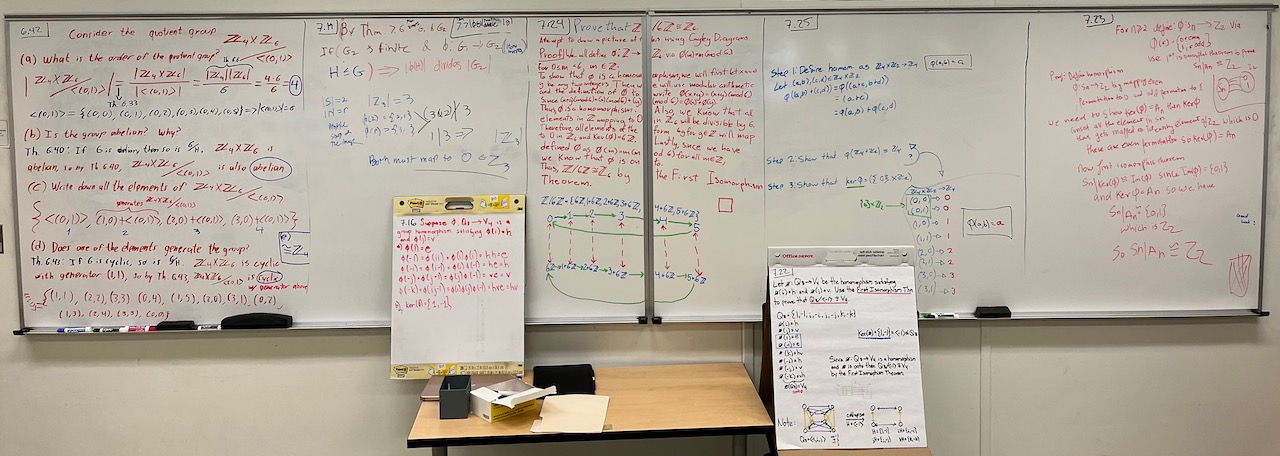
| What we covered: We began by discussing the First Isomorphism Theorem and seeing how it can be viewed as taking a homomorphism of groups and turning it into an isomorphism. After that, we got a lot of stuff on the board, but didn’t have much time to talk through it. We did get to see the details for using the First Isomorphism Theorem to show $Q_8/\langle -1\rangle \cong V_4$, but the rest was saved for next time. We’ll also check in about the final exam next class. |
 |
 |
| Due next class meeting: Nothing! Just start reviewing for the final and bring questions. |
Week 14
[05.02.24] - Thursday
| What we covered: Continued with homomorphisms today getting more into the general theory. For a homomorphism $\phi:G\rightarrow H$, we saw results like $|\phi(g) |$ divides $|\phi(g) |$ for all $g\in G$, that $\operatorname{ker}(\phi)$ is a normal subgroup of $G$, and that $\phi$ is one-to-one iff $\operatorname{ker}(\phi) = \{e\}$. We also computed the kernel and range in a concrete example. We still have a few of lingering problems (6.42, 7.16, and 7.20) that we’ll cover next time. |
 |
| Due next class meeting: HW26 |
[04.30.24] - Tuesday
| What we covered: Lots more with quotient groups today. We started with a couple of problems making computations in specific quotient groups like $(\mathbb{Z}_2 \times \mathbb{Z}_4)/\langle(0,2)\rangle$…which, incidentally, led to us noticing that $(\mathbb{Z}_2 \times \mathbb{Z}_4)/\langle(0,2)\rangle \cong V_4$. We then proved a couple of theorems about how certain properties of a group are inherited by quotients. Specifically we saw that if $G$ is abelian or is cyclic, then $G/H$ is as well. We wrapped up with a couple of problems on homomorphisms. Homomorphisms will be our last main topic for this semester, but the big result we are working towards will bring us back to quotient groups. More next time! |
 |
 |
| Due next class meeting: HW25 |
Week 13
[04.25.24] - Thursday
| Exam day |
| Due next class meeting: HW24 |
[04.23.24] - Tuesday
| What we covered: Finished up a couple of problems about direct products, and then moved on to quotient groups. We spent some time looking at a quotienting process for Cayley diagrams to build intuition, and then got to the formal definition. We finished by making some computations in a few quotient groups to find the orders of elements. More with quotient groups next time. |
 |
| Due next class meeting: Nothing. Just prep for Exam 2. Good Luck! |
Week 12
[04.18.24] - Thursday
| What we covered: Started by wrapping up a couple of problems about normal subgroups, one of which showing that $\langle(1,2,3)\rangle$ is not a normal subgroup of $A_4$. We then moved to direct products of groups. In the first first few examples, we saw that $\mathbb{Z}_2 \times \mathbb{Z}_3 \cong \mathbb{Z}_6$ and $\mathbb{Z}_2 \times \mathbb{Z}_2 \cong V_4$, but $\mathbb{Z}_4 \times \mathbb{Z}_2$ is a group we hadn’t met yet. We looked at orders of elements in direct products, and then unfortunately had to stop before finishing the last few problems. We’ll pick up there next time. |
 |
| Due next class meeting: Look over and try HW23 (and bring questions that you have!), but you will not turn it in. Instead, I will discuss the problems during the next class. Please use the extra time to start preparing for Exam 2. |
[04.16.24] - Tuesday
| What we covered: Started off with Lagrange’s theorem and applications that culminated with a proof that every group of order $p$ is isomorphic to $\mathbb{Z}_p$. We also started discussing normal subgroups, but had to stop before making it through all of the problems. We’ll pick up there next time and also discuss direct products of groups (after which we will return to normal subgroups when we look at quotient groups). |
 |
| Due next class meeting: HW22 |
Week 11
[04.11.24] - Thursday
| What we covered: Started on cosets today, and saw various examples (both finite and infinite). We made several observations early on about the size of cosets and number of cosets that turn out to be general facts. Towards the end we proved two of these: (1) if $H\le G$ and $G$ is abelian, then each left coset of $H$ in $G$ equals the corresponding right coset; and (2) for $H$ a subgroup of $G$, the relation $a\sim b \iff a^{-1}b \in H$ defines an equivalence relation on $G$ (as does $a\sim b \iff ab^{-1} \in H$). |
 |
| Due next class meeting: HW21 |
[04.09.24] - Tuesday
| What we covered: Continued working with permutations, looking at how we can break them down into a product of transpositions. This led to the notion of even and odd permutations and the definition of the alternating group. We finished by observing that $A_3 \cong R_3$ (and also discussed that $A_4$ is not isomorphic to any group we have seen yet). On to cosets next time! |
 |
| Due next class meeting: HW20 |
Week 10
[04.04.24] - Thursday
| What we covered: Took a closer look at $S_n$. We spent a lot of time understanding how to write, think, and compute with cycle notation. We ended with the Cayley diagram for $S_3$ with respect to the generators $(12)$ and $(123)$, which showed us that $S_3$ and $D_3$ are isomorphic. |
 |
| Due next class meeting: HW19 |
[04.02.24] - Tuesday
| What we covered: Wrapped up cyclic groups today with some specialized results about computing orders of elements. Then we got started on permutations and the groups $S_n$, thinking about them as functions and also representing them with string diagrams. Next time we’ll see another way to represent them using “cycle notation.” |
 |
| Due next class meeting: HW18 |
Week 9
[03.28.24] - Thursday
| What we covered: Continued with cyclic groups today. We started with an important result about the order of elements: $g^k=e$ if and only if $|g|$ divides $k$. Next we had a very (perhaps the most) important result about cyclic groups, which is that we know them all: a cyclic group is isomorphic to either the trivial group, $S_2$, $R_n$ (with $n\ge 3$), or $\mathbb{Z}$. After that, we met some new groups $\mathbb{Z}_n$ and $U_n$ using arithmetic modulo $n$ and worked out the details of $\mathbb{Z}_4$, $U_{10}$, and $U_{12}$. One takeaway was that the $\mathbb{Z}_n$ groups are all cyclic; while, the $U_n$ groups sometimes are and sometimes are not. We’ll wrap up cyclic groups next time and start in on a closer look at permutations and the groups $S_n$. |
 |
| Due next class meeting: HW17 |
[03.26.24] - Tuesday
| What we covered: More about cyclic groups today. We started by computing the orders of elements in various groups and then moved to a couple of theoretical results that made concrete much of the intuition we had already developed. When $g$ has finite order, the first result characterized $\langle g \rangle$ as $\langle g \rangle = \{e,g,g^2,\ldots,g^{n-1}\}$, with all elements distinct, for $n$ the smallest positive integer such that $g^n = e$; the second showed that $g^i = g^j$ precisely when $n$ divides $i-j$. Even more about cyclic groups coming! |
 |
| Due next class meeting: HW16 |
Week 8
[$\pi$-Day] - Thursday
| What we covered: Today we started a deeper dive into cyclic groups (and cyclic subgroups of arbitrary groups). We explored some concrete examples, e.g. working out in detail some of the cyclic subgroups of $D_3$, $R_4$, $D_4$, $R_6$, $Q_8$, $\mathbb{Z}$, and $\operatorname{GL}_2(\mathbb{R})$. We also saw proofs that neither $\mathbb{R}$ nor $\operatorname{GL}_2(\mathbb{R})$ are themselves cyclic groups. We finished up by building some general theory around cyclic groups with results like: $\langle g \rangle = \langle g^{-1} \rangle$, that cyclic groups are necessarily abelian, and that if the only subgroups of a group are itself and $\{e\}$, then the group must be cyclic. Time for a week off—enjoy the the break! |
 |
| Due next class meeting: HW15 |
[03.12.24] - Tuesday
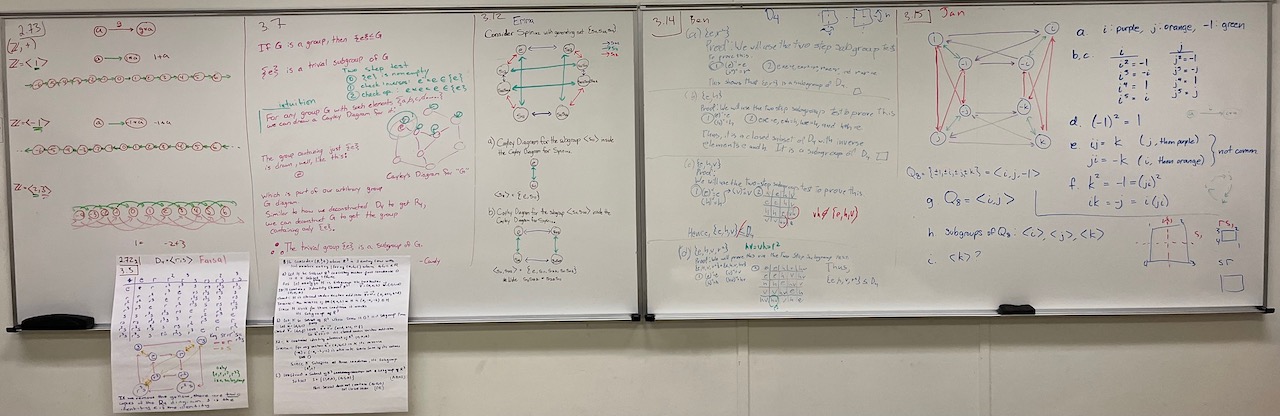
| What we covered: More about isomorphisms today. We saw more examples and nonexamples of isomorphisms as well as more of their properties (like isomorphisms “respect inverses”, they map subgroups to subgroups, and the composition of isomorphisms is again an isomorphism). Underscoring the fact that isomorphic groups are “the same” after renaming elements, we saw an explicit proof that if two groups are isomorphic and one of them is abelian, then the other is too. We also worked with group tables to show that every group of order $4$ is isomorphic to either $R_4$ or $V_4$. |
 |
| Due next class meeting: HW14 |
Week 7
[03.07.24] - Thursday
| Exam day |
| Due next class meeting: HW13 |
[03.05.24] - Tuesday
| What we covered: Started by discussing the idea of “identical table colorings” as another way to see that two groups are really the “same” (complementing the idea of matchings of Cayley diagrams from last time). We then formalized this with the notion of an isomorphism. After a of examples, we had established that $V_4\cong L_2$, $(\mathbb{R},+)\cong (\mathbb{R}^+,\cdot)$, $(\mathbb{Z},+)\cong (2\mathbb{Z},+)$, and that every group of order $3$ is isomorphic to $R_3$. We also explored some properties of isomorphisms, like that they must map the identity of one group to the identity of the other. More next week! Good luck preparing for the exam on Thursday! |
 |
 |
| Due next class meeting: Nothing. Just prep for Exam 1. Good Luck! |
Week 6
[02.29.24] - Thursday
| What we covered: Started with more subgroup lattices today. We’ve now seen them for $R_6$, $S_3$, $D_4$, and $Q_8$. We then started to build intuition about the upcoming concept of isomorphism by looking for “matchings”. With more than just a little effort, we were able to find a matching between $D_4$ and $\operatorname{Spin}_{1\times 2}$ by using the generating set $\{f, s_{11}\}$ for $\operatorname{Spin}_{1\times 2}$ where $f = s_{12}s_{22}$. Our last two problems introduced the “lightswitch groups” $L_2$ and $L_3$. We saw that $L_2$ and $V_4$ can be matched, but $L_3$ is honestly different than any group we’ve met so far. Great day—thanks! |
 |
| Due next class meeting: Look over and try HW12 (and record questions that you have!), but you will not turn it in. Instead, I will discuss the problems during the next class. Try to use the extra time to start preparing for the exam. |
[02.27.24] - Tuesday
| What we covered: Covered a lot of ground with subgroups today. We saw multiple examples of subgroups of $(\mathbb{R}^3,+)$ and also saw that $n\mathbb{Z}$ is a subgroup of $(\mathbb{Z},+)$ for each $n$. Exploring subgroup lattices, we saw that if $H$ and $K$ are subgroups of $G$, then so is $H\cap K$…but typically not $H\cup K$. We ended by determining all subgroups of $D_4$ and building the subgroup lattice. Thanks all! |
 |
| Due next class meeting: HW11 |
Week 5
[02.22.24] - Thursday
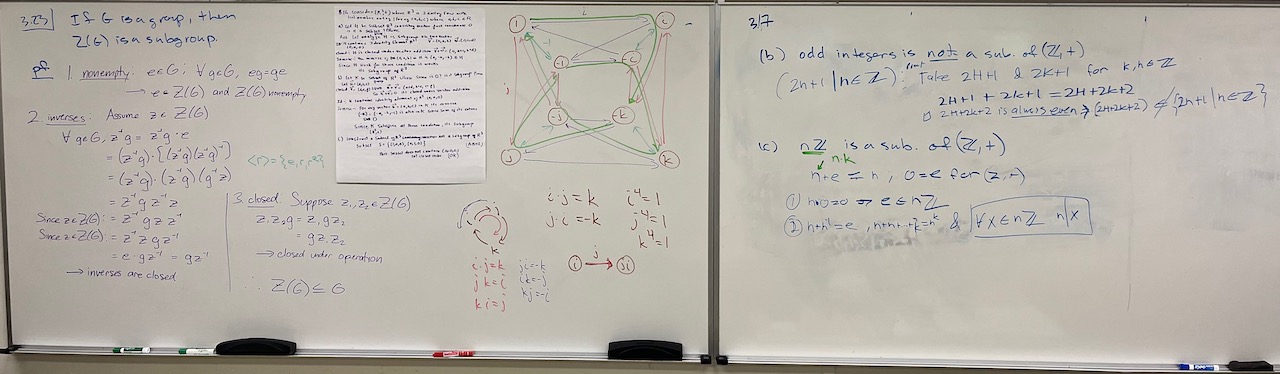
| What we covered: Started by talking through some of the subtleties from the last writing assignment. Then we had a long discussion about the center of a group; we clarified the definition, discussed alternative language, looked at some examples, and finally showed that in order to show $z$ commutes with all elements of $G$ it suffices to just show $z$ commutes with the elements of some generating set for $G$. We didn’t have much time to cover new problems, but we did see a proof that $Z(G)$ is a subgroup of $G$. More next time! |
 |
| Due next class meeting: HW10 |
[02.20.24] - Tuesday
| What we covered: Continued exploring Cayley diagrams, which then led naturally into subgroups. We focused on building intuition about the idea of a subgroup by looking for groups inside other groups (like seeing the diagram for $R_4$ inside the diagram for $D_4$), but we also started practicing how to formally prove if a subset is a subgroup or not. We had to save a couple of problems for Thursday (including the one with our new friend $Q_8$). Thanks for another great day you all! As we’ve noticed several times, the computing of group tables is highly prone to errors. The one for $D_4$ in the picture below is really close, but there are still a couple of small errors to address. (Can you find them?) Working from the one in the picture, I made some edits, and compiled the table here: Group Table for $D_4$. |
 |
| Due next class meeting: HW09 |
Week 4
[02.15.24] - Thursday
| What we covered: Started by finishing our talk about group tables from last time. We met the group $V_4$ (and it’s group table), and also proved a theorem about the structure of group tables: an element can only appear once in any given row and only once in any given column. Next, we discussed Cayley diagrams and explored ones for $\operatorname{Spin}_{1\times2}$, $R_6$, and $D_3$. We’ll create another one or two next time, and then it’s on to subgroups. |
 |
| Due next class meeting: HW08 |
[02.13.24] - Tuesday
| What we covered: We began with a proof that $S_3 = \langle s_1,s_2 \rangle$ and then moved to group tables. There was lots to discuss, and we only made it through the tables for $R_4$, $S_3$, and $S_2$, with a few words about $D_4$ too. In trying to simplify the computations for the tables, we started to take note of the key relations for each of these groups. For example, in $R_4$ the main relation is that $r^4 = e$. In $S_3$, we have $s_1^2 = e$ and $s_2^2 = e$ together with the relation $s_1s_2s_1 = s_2s_1s_2$ describing the interaction of the two generators. For $S_2$, we really just have $s^2 = e$. We’ll revisit $D_4$ next time, but we did take note that there we have $r^4 = e$, $s^2 = e$, and $sr = r^{-1}e$ (which then also implies that $sr = r^{3}e$). Sorry we ran out of time today, but we had great discussions. Thanks all! |
 |
| Due next class meeting: HW07 |
Week 3
[02.08.24] - Thursday
| What we covered: The focus was on generating sets today. We saw that $R_4 = \langle r \rangle$, $D_3 = \langle r,s \rangle = \langle s,s’ \rangle$, and $\mathbb{Z} = \langle 1\rangle = \langle -1\rangle$. Didn’t get to $S_3$ this time, but next time we’ll see that $S_3 = \langle s_1,s_2 \rangle$ (which will further highlight similarities between $D_3$ and $S_3$). Fun day! |
 |
 |
| Due next class meeting: HW06 |
[02.06.24] - Tuesday
| What we covered: Started with a closer look at $S_3$ to see that it is indeed a group and it is not commutative. Then we got into our first proofs for the class, showing things like cancellation, uniqueness of the identity and inverses, and the fact that $(g^{-1})^{-1} = g$ (as one would hope). Another great day—thanks to all! |
 |
| Due next class meeting: HW05 |
Week 2
[02.01.24] - Thursday
| What we covered: Continued our conversation about binary operations, looking at some that were nonassociative…which took a little while for us to see with 2.31 but we finally got there with a team effort! Next, we started exploring the definition of a group by looking at some examples and nonexamples. Not only did we get more comfortable with the abstract notition of a group, but we also continued to clarify some of the specific examples (like $R_4$ and $D_3$) that we’ll use a lot in our course. In the end, we only made it part way through 2.36, so we’ll pick up there next time. Great presentations and excellent questions from the whole group! Thanks for another fantastic day you all! |
 |
| Due next class meeting (02/06): HW04 |
[01.30.24] - Tuesday
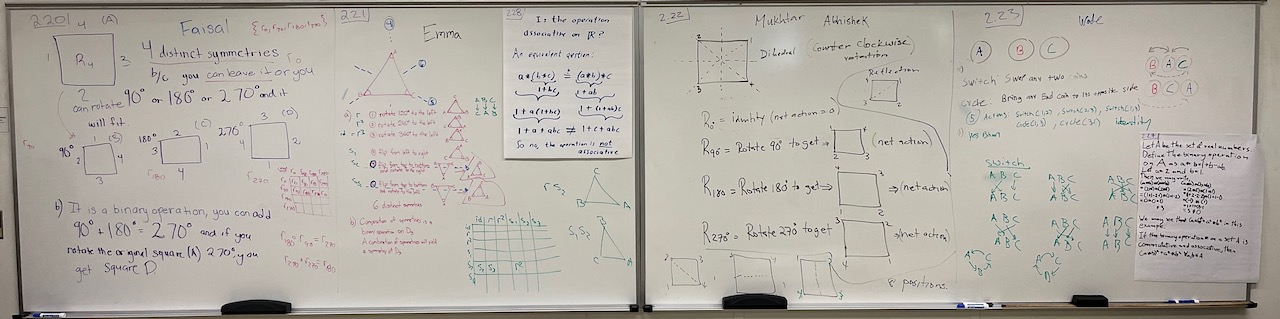
| What we covered: Discussed binary operations today. We spent most of our time getting acquainted with symmetries of certain objects and met the groups $R_4$, $D_3$, $D_4$, and $S_3$. We didn’t quite get to all of the problems, so we’ll discuss them next time along with the new problems. Photo of our work is below—you can click on it for a larger version. Many thanks to all of the presenters today! …and to everyone else too for such a fun and supportive environment. Looking forward to Thursday! |
 |
| Due next class meeting (02/01): HW03 |
Week 1
[01.24.24] - Thursday
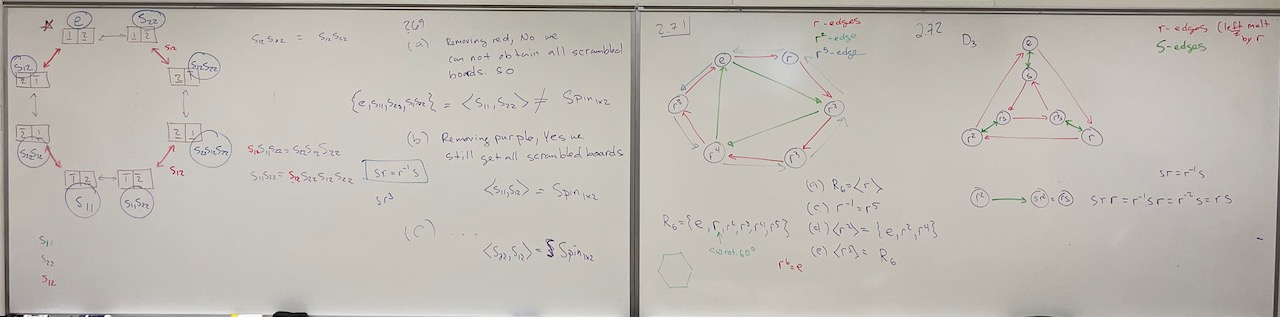
| What we covered: We started by playing a little Spinpossible together and then worked through most of Section 2.1 of our book. We computed the number of Spinpossible boards (presented by JJ–thanks!), found various relations among the actions generated by the spins (like $s_{12}s_{23}s_{12}=s_{23}s_{12}s_{23}$), and (best of all) asked lots more questions. Thanks for a great day you all!! |
| Due next class meeting (01/30): HW02. Remember: try to find/build community to collaborate on these problems, but please avoid using outside resources to solve them. (More info in the syllabus.) |
[01.22.24] - Tuesday
| What we covered: The faculty strike led to a tentative agreement with the CSU management after just one day, so it was quite a surprise that class met. Not everyone could be there, so we didn’t cover any course material. Instead, we did some introductions, chatted about the strike, and then took a look at the syllabus for the class. We’ll definitely repeat introductions on Thursday and review the main structural pieces about the course. |
| Due next class meeting (01/24): Please work on: HW01. Given all the start of semester turmoil, you will not be graded on this assignment, but we will talk about it in class. Also, if you couldn’t make it to class on Tuesday, please read over the syllabus. |
