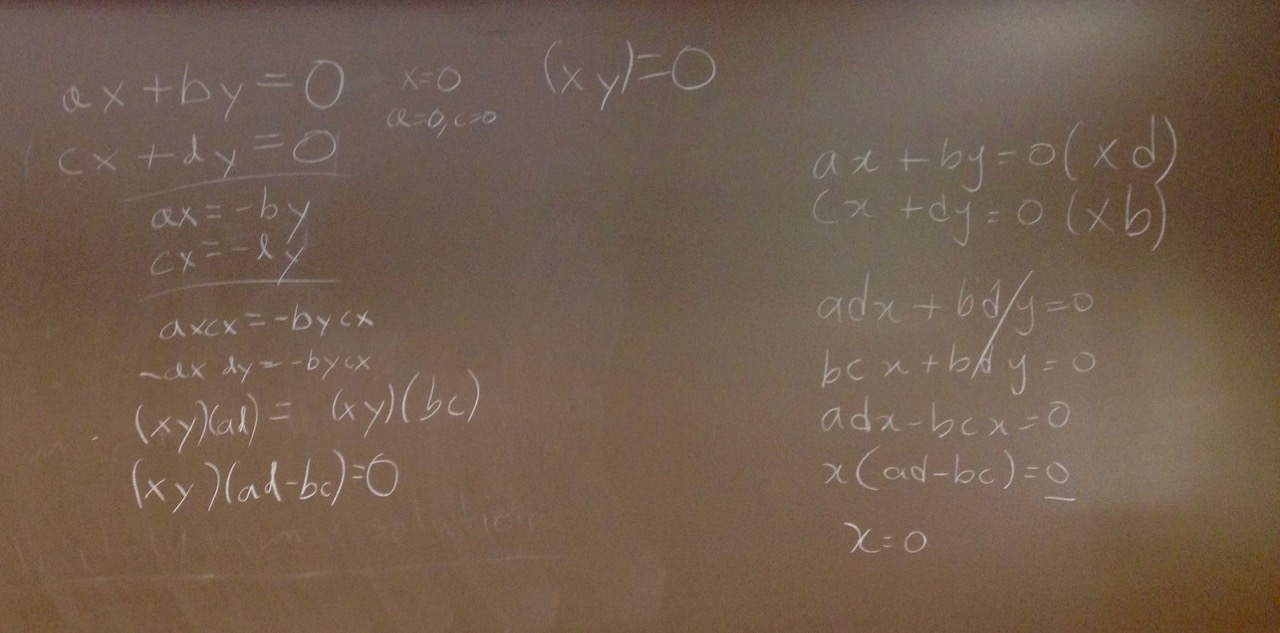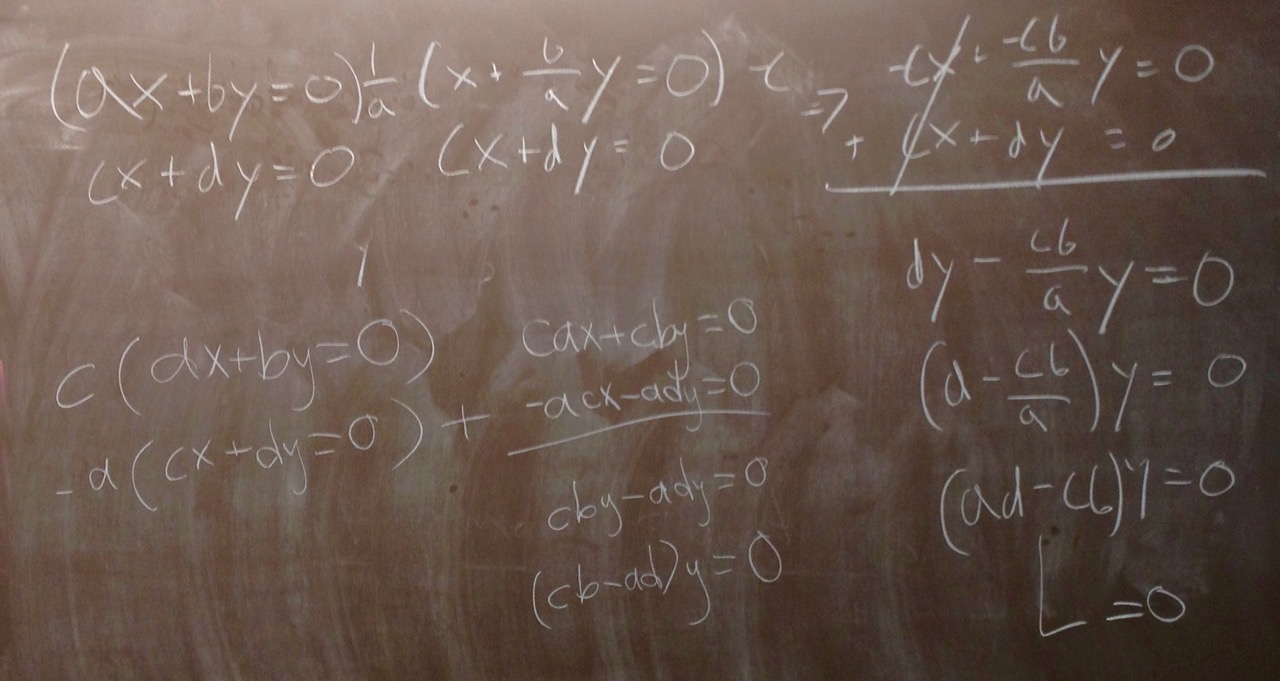| Week 1 |
|---|
|
[01.20.16] - Wednesday - First day!
Started with a discussion about super powers we wish we had and non-math skills we do have. Then we talked about what we even mean by "mathematical skill." No one said "the ability to solve hard problems." Instead, we wrote down some of the actual skills that enable us to solve hard problems (and communicate them to others).


- Math skills to hone -
(Please ignore my typos!)
|
|
Sections covered: 1.1 (started)
|
Reading for next time: Section 1.1. Focus on the following:
- the definitions, which are in bold. (Trivial solution, consistent system, and homogeneous system will be used a lot in this course.)
- Examples 3, 4, and 5
- Blue Box on Page 6
- Last paragraph of the section on page 8
|
To discuss next time:
- What are the differences between the linear systems in Examples 3, 4, and 5 in terms of the set of solutions? Are there any similarities?
- Prove (or at least be prepared to discuss where you got stuck in proving) the following proposition:
Proposition. Let $a,b,c,d$ be arbitrary real numbers. If $ad-bc \neq 0$, then the homogeneous system
\[
\begin{array}{rcrcr}
ax & + &by & = & 0\\
cx & + & dy & = & 0
\end{array}
\]
has only the trivial solution.
|
|
[01.22.16] - Friday
Started with great presentations and many excellent comments from the audience! We then talked a bit about the differences between presenting proofs at the board and writing up proofs on paper. Here's a link to the written model I presented today: Proof Model 1.
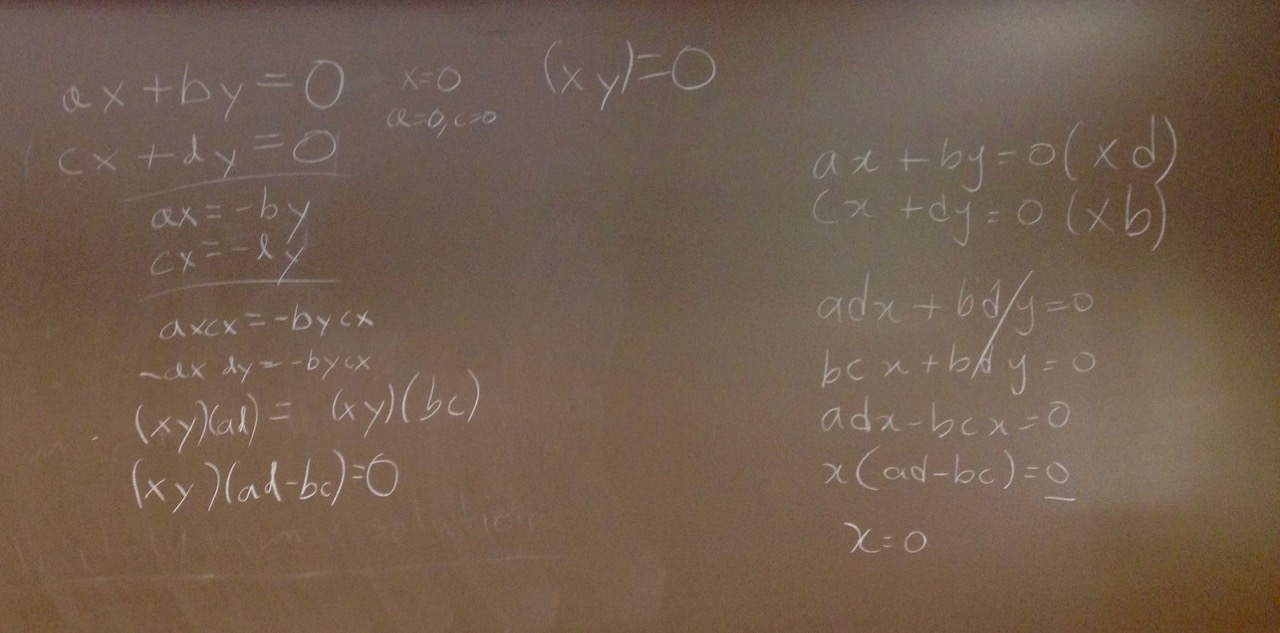
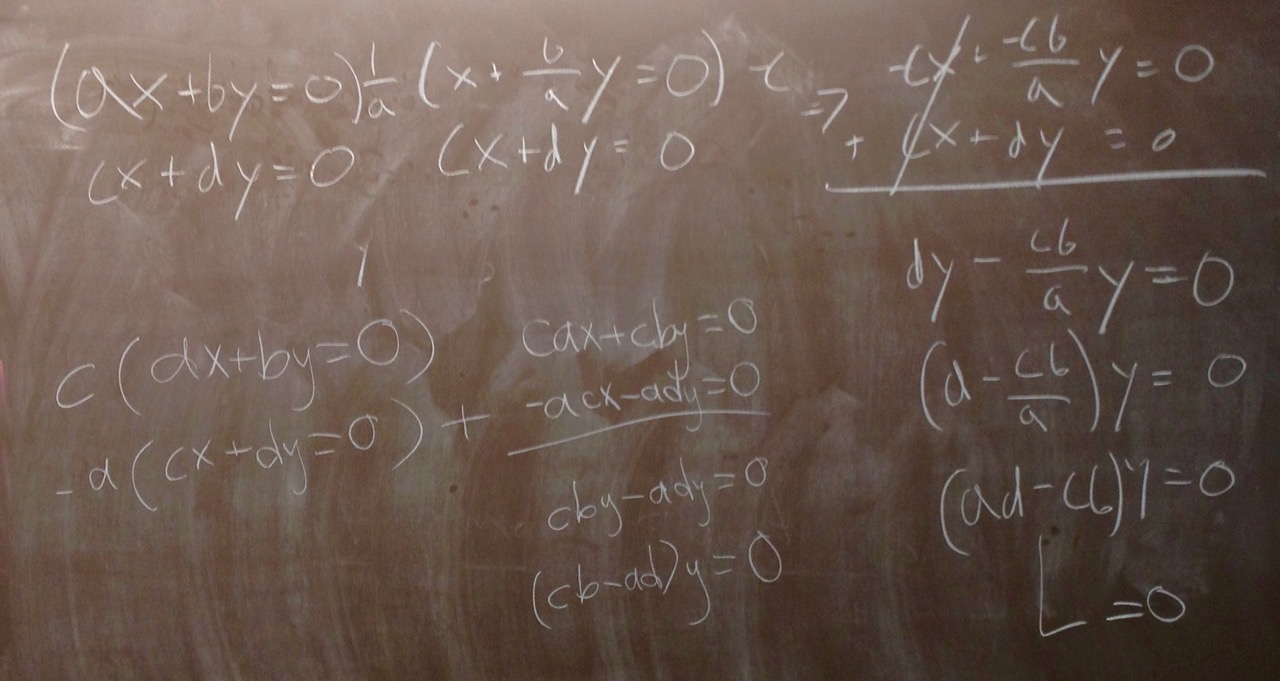
- Solving problems! -
(each picture has two different approaches)
|
|
Sections covered: 1.1 (finished), 1.2 (started)
|
Reading for next time: Section 1.2. Focus on the following:
- the definitions, paying special attention to $\mathbb{R}^n$, linear combination, and traspose
- notation for matrices, e.g. $A = [a_{ij}]$
- summation notation
|
To discuss next time:
- When we write "let $A=[a_{ij}]$ be an $m\times n$ matrix," what is the difference between $[a_{ij}]$ and $a_{ij}$?
- True or False: every vector in $\mathbb{R}^3$ can be written as a linear combination of the following three vectors: \[\begin{bmatrix}1\\0\\0\end{bmatrix}, \begin{bmatrix}0\\1\\0\end{bmatrix}, \begin{bmatrix}0\\0\\1\end{bmatrix}\]
- True or False: every vector in $\mathbb{R}^3$ can be written as a linear combination of the following three vectors: \[\begin{bmatrix}1\\0\\0\end{bmatrix}, \begin{bmatrix}0\\2\\0\end{bmatrix}, \begin{bmatrix}3\\4\\0\end{bmatrix}\]
|
|
[01.25.16] - Monday
Another fantastic day with excellent presentations (many thanks to the brave volunteers!) and superb audience participation. Great job!
|
| Sections covered: 1.2 (finished), 1.3 (started) |
Reading for next time: Section 1.3. Focus on the following:
- the definitions, paying special attention to the definition of matrix multiplication (Def. 1.7)
- Example 9
- the discussion about a matrix-vector product (between examples 11 and 12)
- Examples 11, 12
|
To discuss next time:
- True or False: if $A$ and $B$ are any (arbitrary) $3\times 3$ matrices, then $AB=BA$.
- True or False: if $A$ and $B$ are any $2\times 2$ matrices such that $AB = 0_{2\times 2}$, then it must be that either $A = 0_{2\times 2}$ or $B = 0_{2\times 2}$. Note: here $0_{2\times 2}$ denotes the $2\times 2$ zero matrix, i.e. \[0_{2\times 2} = \begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}.\]
- True or False: if $A$ is any $2\times 2$ matrix and $c\in \mathbb{R}$ is any scalar such that $cA = 0_{2\times 2}$, then it must be that either $A = 0_{2\times 2}$ or $c=0$.
|
[01.27.16] - Wednesday
Stellar presentations and good discussion again! Thanks!
Also, another proof model was added to ShareLaTeX. It is here: Proof Model 2.
|
| Sections covered: 1.3 (finished) |
Reading for next time: Section 1.4. Focus on the following:
- the theorems, which tell us that the matrix operations satisfy some familiar properties, e.g. commutativity of addition and associativity of addition and multiplication
- Examples 9 and 10 (and the blue boxes surrounding them), which tells us that some familiar properties are not true (in general)
|
To discuss next time:
- Bring in your (typed up, if possible) solution to #28(b) from 1.3; make sure that it is a formal write-up with all variables properly defined, correct punctuation, etc. Be prepared to talk through it on the document camera.
|
|
[01.29.16] - Friday
Today we began by discussing the structure and goals for a formal proof write-up (in contrast to a "regular" homework assignment or board work). Many thanks to those who presented their proofs. They were great!
|
| Sections covered: 1.4 |
Reading for next time: Section 1.5 up through Example 12. You can skip the subsection on "Partitioned Matrices," though this idea can be really useful sometimes. Focus on the following:
- the definitions, paying special attention to invertible (nonsingular) and inverse
- Examples 11 and 12
|
To discuss next time:
- Give an example of a $2\times 2$ matrix that is not the zero matrix and is not invertible.
- If $A$ is an $n\times n$ diagonal matrix such that every entry on the main diagonal is nonzero, show that $A$ is invertible. Hint: to do this, you just have to write down what the inverse is and then check that it works. If you have trouble seeing it, try experimenting in the $2\times 2$ world first.
|
| Week 3 |
|---|
|
[02.01.16] - Monday
|
|
Sections covered: 1.4 (finished), 1.5 (started)
|
Reading for next time: Section 1.5 from Theorem 1.6 through Example 14. Focus on the following:
- Theorem 1.6
- Examples 14
|
To discuss next time:
- Take another crack at this one: if $A$ is an $n\times n$ diagonal matrix such that every entry on the main diagonal is nonzero, show that $A$ is invertible. Hint: take an educated guess at what the inverse is (based on class today), and call it $B$. To show that $B$ is indeed the inverse, you just need to show that $AB = I$ and $BA = I$ (the remark between Definition 1.10 and Example 10 simplifies this further).
- Let $A = \begin{bmatrix} 2 & 3\\ 5 & 7\end{bmatrix}$. First, show that $B = \begin{bmatrix} -7 & 3\\ 5 & -2\end{bmatrix}$ is the inverse of $A$. Hint: you just need to show that $AB = I$. Second, use that $B = A^{-1}$ to quickly solve $\begin{bmatrix} 2 & 3\\ 5 & 7\end{bmatrix} \begin{bmatrix} x_1 \\ x_2\end{bmatrix} = \begin{bmatrix} 1\\ 1\end{bmatrix}$ (as in Example 14).
|
|
[02.03.16] - Wednesday
Great day! One of the highlights of the discussion was the proof of the following theorem, which you can now use in any future work.
Theorem (Jon-Jenny-Atticus). If $A =[a_{ij}]$ is an $n\times n$ diagonal matrix such that every entry on the main diagonal is nonzero, then $A$ is invertible and \[A^{-1} = \begin{bmatrix} \frac{1}{a_{11}} & 0 &\cdots & 0\\ 0 & \frac{1}{a_{22}} & \cdots & 0\\ \vdots & & \ddots & \vdots\\ 0 & 0 & \cdots & \frac{1}{a_{nn}}\end{bmatrix}.\]
|
|
Sections covered: 1.5
|
Reading for next time: Section 1.6. Focus on the following:
- the discussion on the top half of page 57 (pay attention to the definitions)
- Examples 2 and 3
|
To discuss next time:
- Bring in your typed up solution to AP #2; make sure that it is a formal write-up that is fully justified with correct punctuation.
|
|
[02.05.16] - Friday
|
|
Sections covered: 1.6
|
Reading for next time: The logic notes of Professor Gibbons: beginning through Theorem 1.16. Focus on the following:
- the definitions, e.g. statement, negation, conjunction, disjunction, implication, logically equivalent
- the examples
- De Morgan's Laws, Law of Double Negation, Law of Implication
|
|
To discuss next time: Download and print out this worksheet. Be able to discuss the first two problems when you come to class. Of course, you can think about them all, but the rest can be completed in class.
|
| Week 4 |
|---|
|
[02.08.16] - Monday You all are amazing! I couldn't be in class today (for which I'm very sorry), and I was very impressed (but not at all surprised) to see that you don't need me at all. Great job!! See you soon.


- No Josh! -
|
|
Sections covered: Logic (started)
|
Reading for next time: The logic notes: Definition 1.17 through Example 2.4. Focus on the following:
- the definitions
- Examples 1.18, 2.2, 2.4
|
|
To discuss next time: There may not be a formal discussion on Wednesday, but make sure to be involved. Class will be in the exceptionally capable hands of Professors Dykstra and Gibbons. See you Friday!
|
|
[02.10.16] - Wednesday
|
|
Sections covered: Logic (continued)
|
Reading for next time: The logic notes: Section 3 (starting at the bottom of page 7 and continuing through page 9. Focus on the following:
- the definitions
- Examples 3.1, 3.2, 3.3, 3.4
|
|
To discuss next time: Bring you questions about Examples 3.1, 3.2, 3.3, and 3.4. We will discuss all of these in class taking time to highlight both the structure (because that's really what this section is all about) and the content.
|
|
[02.12.16] - Friday
|
|
Sections covered: Logic (continued)
|
Reading for next time:
- Start by reading Theorem 2.3 on page 96. It contains terms that we haven't defined yet, but it motivates Section 2.1.
- Look back, if needed, to remember how we change between linear systems and augmented matrices (see pg 27-28).
- Read Definitions 2.2 and 2.3 in Section 2.1, and then read Examples 3 and 4 in Section 2.1.
|
To discuss next time:
- Do you see similarities between the manipulations we do to solve linear systems (see blue box on page 6) and the elementary row operations? Differences?
- Consider the following linear system: \[\begin{align*}x_2 + x_3 &= 2\\x_1 + x_3 &= 1\\-3x_1 + 2x_2 &= 4\end{align*}\]
- Write the augmented matrix corresponding to this linear system.
- Show that the augmented matrix you found is row equivalent to \[ \left[\begin{array}{ccc|c}1 & 0 & 1& 1\\ 0 & 1 & 1& 2\\0 & 0 & 1& 3\end{array}\right].\] That is, use elementary row operations to transform the augmented matrix you found before into this one.
- Write out the linear system corresponding to this new augmented matrix.
|
| Week 5 |
|---|
|
[02.15.16] - Monday
|
|
Sections covered: Logic, 2.1 (started)
|
Reading for next time: Section 2.2. Focus on the following:
- Examples 3, 6, and 10
|
To discuss next time:
- Notice that, as in Example 6, you can stop the reduction process at an REF and solve the system with "back substitution", or you can continue the reduction process to RREF and have the solutions "right there." Which one do you like better? Does one method seem more efficient?
- Suppose you are trying to solve a homogeneous linear system of 3 equations in 4 unknowns. Explain (and don't just quote a theorem) why the system must have infinitely many solutions (regardless of what the system actually looks like).
- Is an arbitrary linear system of 3 equations in 4 unknowns guaranteed to have infinitely many solutions? Why or why not?
|
|
[02.17.16] - Wednesday
|
|
Sections covered: 2.1 (finished), 2.2 (started)
|
|
Reading for next time: Start of Section 2.3, through Example 2. Also read Lemma 2.1 on page 119.
|
To discuss next time: let's make sense of Lemma 2.1. Let $A$ be an $n\times n$ matrix.
- We want to show that if $A\mathbf{x} = \mathbf{0}$ has only the trivial solution, then $A$ is row equivalent to the identity. Suppose $A\mathbf{x} = \mathbf{0}$ has only the trivial solution. Using the language of pivots and free variables, find the RREF of $\left[\begin{array}{c|c}A & \mathbf{0}\end{array}\right]$. (If needed, experiment in the $3\times 3$ case first.) What does this mean about the RREF of $A$?
- Is the converse true? That is, is it true that if $A$ is row equivalent to the identity, then $A\mathbf{x} = \mathbf{0}$ has only the trivial solution?
|
|
[02.19.16] - Friday
|
|
Sections covered: 2.2 (finished), 2.3 (started)
|
Reading for next time: Section 2.3 - Finding $A^{-1}$. Focus on the following:
- pg. 121
- Examples 5 and 6
|
To discuss next time: Let $A$ be an arbitrary $2\times 2$ upper triangular matrix, i.e. \[A=\begin{bmatrix}a & b\\ 0 & c\end{bmatrix}\]
- Complete the following sentence: $A$ is invertible if and only if... (insert some condition on $a$, $b$, and $c$)
Hint: Think about what you read; there is an algorithm for finding $A^{-1}$. When does the algorithm succeed for this particular $A$ (or, alternatively, what could make it fail)?
- What if $A$ had been an arbitrary $n\times n$ upper triangular matrix? Complete the following sentence for the $n\times n$ case: $A$ is invertible if and only if... (insert some condition on the entries of $A$)
|
| Week 6 |
|---|
|
[02.22.16] - Monday
|
|
Sections covered: 2.3 (finished), 3.1 (started)
|
Reading for next time: Section 3.1. Focus on the following:
- Intro. through Example 5. (For the record, I find Example 1 confusing, which motivated the discussion questions below.)
|
To discuss next time:
- How do you visualize a permutation? If you're at a loss, try googling "permutation."
- How many permutations are there of the set $\{1,2,3,4\}$, i.e. how many ways are there to arrange the numbers $1,2,3,4$? (Yes, the answer is in the book. But, I want each of you to understand it and be able to clearly explain it.)
- Is the permutation 4321 even or odd? Be able to identify the inversions.
|
|
[02.24.16] - Wednesday
Lots of nice presentations and discussion today. Great job! Here is one of the things that came out of it.
Theorem (Mike-Ryan). If $A$ is an $n\times n$ upper or lower triangular matrix, then $A$ is invertible if and only if every entry on the main diagonal of $A$ is nonzero.
|
|
Sections covered: 3.1
|
Reading for next time: Section 3.2. Focus on the following:
- Read the statements of the Theorems, but you can skip the proofs for now.
|
To discuss next time: let's make a review sheet for the midterm.
- Please construct one question of the form "provide a specific example which satisfies the given description, or if no such example exists, briefly explain why not" and add it to our review sheet here
https://www.sharelatex.com/project/56ce03263a091c210d42ed9a
The review sheet already contains a question I made that you can use as an example.
Make sure to
- put your initials next to your questions, and
- put an answer in the "Answers" section of the document (again, I provided an example).
- Repeat with a T/F question.
- Make sure to write down your questions and answers on paper too, so you are prepared to present them in class.
|
|
[02.26.16] - Friday
Excellent job on the review sheet!! Here's (a slightly edited version of) what you made:
Exam1ReviewQuestions.pdf
|
|
Sections covered: 3.2 (started)
|
|
Reading for next time: None. Focus on studying.
|
| Week 7 |
|---|
|
[02.29.16] - Monday Remember that the first midterm exam is tomorrow evening. It will cover oll of the material we talked about up through Section 2.3 (including logic). Happy studying!
|
|
Sections covered: 3.2 (finished)
|
Reading for next time: First, study for the exam! Then read Section 3.3. Focus on the following:
- Example 2 in Section 3.3.
|
To discuss next time: Properties of the determinant.
- Let $A\in M_{n\times n}$, and assume that $A$ is invertible with $A=A^{-1}$. What are the possible values for $\operatorname{det}(A)$?
|
|
[03.02.16] - Wednesday
|
|
Sections covered: 3.3
|
Reading for next time: Section 4.2. Focus on the following:
- Examples 1, 2, 5, 6, 11 (and the blue box following Example 11)
- The proof of Theorem 4.2(a)
|
To discuss next time:
- Let $V$ be the set of all $2\times 2$ matrices (with entries from $\mathbb{R}$) that have determinant $0$. Define $\oplus$ to be ordinary matrix addition, and $\odot$ to be ordinary scalar multiplication. Is $V$ closed under $\oplus$ (see Definition 4.4(a))? That is, is it true that for all $A,B\in V$, $A+B \in V$? Is $V$ closed under $\odot$ (see Definition 4.4(b))?
- Digest the proof of Theorem 4.2(a). Use a similar idea to prove Theorem 4.2(b).
|
|
[03.04.16] - Friday
|
|
Sections covered: 4.2 (started)
|
Reading for next time: Section 4.2. Focus on the following:
- Examples 7, 9, 10
|
To discuss next time: Revisit the questions from last time. (If you haven't presented in class yet, Monday would be a great day for it; there are three to do.)
- Let $V$ be the set of all $2\times 2$ matrices (with entries from $\mathbb{R}$) that have determinant $0$. Define $\oplus$ to be ordinary matrix addition, and $\odot$ to be ordinary scalar multiplication. Is $V$ closed under $\oplus$ (see Definition 4.4(a))? That is, is it true that for all $A,B\in V$, $A+B \in V$? Is $V$ closed under $\odot$ (see Definition 4.4(b))?
- Digest the proof of Theorem 4.2(a). Use a similar idea to prove Theorem 4.2(b).
|
| Week 8 |
|---|
|
[03.07.16] - Monday
|
|
Sections covered: 4.2 (finished), 4.3 (started)
|
Reading for next time: Section 4.3. Focus on the following:
- Definition 4.5 through Theorem 4.3 (put your focus on Theorem 4.3)
- Examples 1-4
|
To discuss next time:
- We learned that $M_{2\times 2}$ is a vector space. Let $W$ be the subset of $M_{2\times 2}$ consisting of the $2\times 2$ matrices whose trace is $0$, i.e. $W=\{A \in M_{2\times 2} \,|\, \operatorname{tr}(A) = 0\}$. Use Theorem 4.3 to show that $W$ is a subspace of $M_{2\times 2}$.
|
|
[03.09.16] - Wednesday
|
|
Sections covered: 4.3 (continued)
|
Reading for next time: Section 4.3. Focus on the following:
- Examples 6-9 and Definition 4.6
|
To discuss next time:
- Be able to write on the board, from memory, the definition of a linear combination of vectors $v_1,\ldots,v_k$. I may call on multiple people for the same definition!
- After reading Example 7 and looking over Figure 4.22, describe algebraically and geometrically the set of all linear combinations of the following two vectors in $\mathbb{R}^3$: \[\mathbf{v_1} = \begin{bmatrix}\pi\\0\\0 \end{bmatrix}\text{ and } \mathbf{v_2} = \begin{bmatrix}0\\0\\e \end{bmatrix}.\]
|
|
[03.11.16] - Friday
|
|
Sections covered: 4.3
|
Reading for next time: Section 4.4. Focus on the following:
- Definition 4.7, Definition 4.8, and the remark following Definition 4.8
- Examples 1, 2, 5, 7, 8
|
To discuss next time: (Make sure to read Example 7 first.)
- Consider the following four vectors in $P_3$
\[\mathbf{v}_1 = 1+2t+3t^3,\quad \mathbf{v}_2 = 3+t+t^2-t^3,\quad \mathbf{v}_3 = -5t-t^2-t^3,\quad \mathbf{v} = -2-14t-2t^2-8t^3.\]
Suppose you want to determine if $\mathbf{v}$ is in $\operatorname{span}\{\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3\}$.
- Explain why this is the same as determining if the following system is consistent.
\[\left[\begin{array}{rrr|r}1 & 3 & 0 & -2\\ 2 & 1 & -5 & -14\\0 & 1 & -1 & -2\\ 3 & -1 & -1 & -8\end{array}\right]\]
- Is $\mathbf{v}\in\operatorname{span}\{\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3\}$?
- Consider the following four vectors in $M_{2 \times 2}$
\[\mathbf{v}_1 = \begin{bmatrix}0 & 2\\ 3 & 0 \end{bmatrix},\quad \mathbf{v}_2 = \begin{bmatrix}1 & -1\\ 3 & -1 \end{bmatrix},\quad \mathbf{v}_3 = \begin{bmatrix}\pi & 0\\ 0 & -\pi \end{bmatrix},\quad \mathbf{v} = \begin{bmatrix}1 & 2\\ 3 & 4 \end{bmatrix}.\] Suppose you want to determine if $\mathbf{v}$ is in $\operatorname{span}\{\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3\}$.
- Explain why this is the same as determining if the following system is consistent.
\[\left[\begin{array}{rrr|r}0 & 1 & \pi & 1\\ 2 & -1 & 0 & 2\\3 & 3 & 0 & 3\\ 0 & -1 & -\pi & 4\end{array}\right]\]
- Is $\mathbf{v}\in\operatorname{span}\{\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3\}$?
|
| Week 9 |
|---|
|
|
|
[03.28.16] - Monday
|
|
Sections covered: 4.4 (continued)
|
Reading for next time: Section 4.5. Focus on the following:
- Definition 4.9
- Examples 2, 6
|
To discuss next time: Let $\mathbf{u} = \begin{bmatrix} 1\\ 2\\ \pi \end{bmatrix}$.
- Is $\{\mathbf{u}, \mathbf{0}\}$ linearly dependent?
- Find three different choices for $\mathbf{v}\in \mathbb{R}^3$ for which $\{\mathbf{u}, \mathbf{v}\}$ is linearly dependent.
- Can you find all vectors $\mathbf{v}\in \mathbb{R}^3$ for which $\{\mathbf{u}, \mathbf{v}\}$ is linearly dependent?
|
|
[03.31.16] - Wednesday
|
|
Sections covered: 4.4 (finished), 4.5 (started)
|
Reading for next time: Section 4.5. Focus on the following:
- Theorem 4.7 (compare this with what you proved on the last writing assignment, see Remark 2 following Example 10)
- Remarks 1-3 following Example 10 (also compare Remark 3 with what you proved on the last writing assignment)
|
To discuss next time: Carry over from last time plus a little more:
- Be able to write on the board, from memory, the definition of linearly independent vectors $v_1,\ldots,v_k$. I may call on multiple people for the same definition!
- Let $\mathbf{u} = \begin{bmatrix} 1\\ 2\\ \pi \end{bmatrix}$.
- Is $\{\mathbf{u}, \mathbf{0}\}$ linearly dependent?
- Find three different choices for $\mathbf{v}\in \mathbb{R}^3$ for which $\{\mathbf{u}, \mathbf{v}\}$ is linearly dependent.
- Can you find all vectors $\mathbf{v}\in \mathbb{R}^3$ for which $\{\mathbf{u}, \mathbf{v}\}$ is linearly dependent?
|
|
[04.01.16] - Friday
Lots of nice presentations and discussions today! Nice job.
|
|
Sections covered: 4.5 (almost finished)
|
Reading for next time: Section 4.6. Focus on the following:
- Definition 4.10
- Example 1
|
To discuss next time:
- Is $\left\{ \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix}, \begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix}\right\}$ a basis for $\mathbb{R}^3$? Why or why not?
- Is $\left\{ \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix}, \begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix}, \begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}, \begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix}\right\}$ a basis for $\mathbb{R}^3$? Why or why not?
- Is $\left\{ \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix}, \begin{bmatrix} 1\\ 1\\ 0 \end{bmatrix}, \begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix}\right\}$ a basis for $\mathbb{R}^3$? Why or why not?
|
| Week 10 |
|---|
|
|
|
[04.04.16] - Monday Great presentations today with nice audience involvement. Love it!
|
|
Sections covered: 4.5 (finished), 4.6 (started)
|
Reading for next time: Section 4.6. Focus on the following:
- Definition 4.10
- Examples 2 and 4
|
To discuss next time: Let $\mathbf{v}_1$, $\mathbf{v}_2$, $\mathbf{v}_3$, $\mathbf{v}_4$ be arbitrary vectors in $P_2$. Thus
\[
\begin{align}
\mathbf{v}_1 & = a_1+b_1t+c_1t^2\\
\mathbf{v}_2 & = a_2+b_2t+c_2t^2\\
\mathbf{v}_3 & = a_3+b_3t+c_3t^2\\
\mathbf{v}_4 & = a_4+b_4t+c_4t^2
\end{align}
\] for some $a_i,b_i,c_i \in \mathbb{R}$
- Explain, in detail, why determining if $\{\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3, \mathbf{v}_4\}$ is linearly independent is the same as determining if the following system has only the trivial solution:
\[
\left[\begin{array}{cccc|c}
a_1 & a_2 & a_3 & a_4 & 0\\
b_1 & b_2 & b_3 & b_4 & 0\\
c_1 & c_2 & c_3 & c_4 & 0\\
\end{array}\right]
\]
- By considering the RREF (i.e. think about pivots and free variables), explain why $\{\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3, \mathbf{v}_4\}$ is linearly dependent (no matter what $\mathbf{v}_1$, $\mathbf{v}_2$, $\mathbf{v}_3$, $\mathbf{v}_4$ actually are).
- Explain, in detail, why determining if $\{\mathbf{v}_1, \mathbf{v}_2\}$ spans $P_2$ is the same as determining if the following system is consistent for all choices of $e,f,g\in \mathbb{R}$:
\[
\left[\begin{array}{cc|c}
a_1 & a_2 & e\\
b_1 & b_2 & f\\
c_1 & c_2 & g\\
\end{array}\right]
\]
- By considering the RREF, explain why $\{\mathbf{v}_1, \mathbf{v}_2\}$ does not span $P_2$ (no matter what $\mathbf{v}_1$ and $\mathbf{v}_2$ actually are).
- Explain the following statement: "every basis for $P_2$ has the same number of vectors and that number is $\underline{\phantom{XXXX}}$".
|
|
[04.06.16] - Wednesday
|
|
Sections covered: 4.6 (continued)
|
Reading for next time: Section 4.6. Focus on the following:
- Blue box on page 235
- Example 6
|
To discuss next time:
- Let $v_1 = \begin{bmatrix} 1\\ -1\\ 1\\ 0 \end{bmatrix}$, $v_2 = \begin{bmatrix} 2\\ -1\\ -1\\-1 \end{bmatrix}$, $v_3 = \begin{bmatrix} 3\\ -6\\ 12\\ 3 \end{bmatrix}$, and $v_4 = \begin{bmatrix} 4\\ -3\\ 2\\-\frac{1}{2} \end{bmatrix}$. Follow the process in the blue box on page 235 to find a basis for $W = \operatorname{span}\{v_1, v_2, v_3, v_4\}$.
|
|
[04.08.16] - Friday
|
|
Sections covered: 4.6 (finished)
|
Reading for next time: Section 4.8. Focus on the following:
- Introduction
- Example 1 and 2
|
To discuss next time:
- Let $B_1$ be the following ordered basis for $P_2$: $B_1 = \{t^2,t,1\}$.
- Explain why $\left[3t^2 + 2\right]_{B_1} = \begin{bmatrix} 3\\ 0\\ 2 \end{bmatrix}$.
I'll answer this one, but make sure you understand my reasoning...
Define $\mathbf{b}_1 = t^2$, $\mathbf{b}_2 = t$, and $\mathbf{b}_3 = 1$; thus, $B_1 = \{\mathbf{b}_1, \mathbf{b}_2, \mathbf{b}_3\}$. Now, observe that $3t^2 + 2 = 3\cdot \mathbf{b}_1 + 0\cdot\mathbf{b}_2 + 2\cdot \mathbf{b}_3$, and this implies that $\left[3t^2 + 2\right]_{B_1} = \begin{bmatrix} 3\\ 0\\ 2 \end{bmatrix}$.
- Let $B_2$ be the following ordered basis for $P_2$: $B_2 = \{t,1,t^2\}$.
- Explain why $\left[3t^2 + 2\right]_{B_2} = \begin{bmatrix} 0\\ 2\\ 3 \end{bmatrix}$.
- Let $B_3$ be the following ordered basis for $P_2$: $B_3 = \{t^2+t+1,t^2+t,t^2\}$.
- Explain why $\left[3t^2 + 2\right]_{B_3} = \left[\begin{array}{r} 2\\ -2\\ 3 \end{array}\right]$.
|
| Week 11 |
|---|
|
[04.11.16] - Monday
|
|
Sections covered: 4.8 (started)
|
Reading for next time: Section 4.8. Focus on the following:
- Introduction to transition matrices (pages 261-262)
- Example 4
|
To discuss next time: Let $A\in M_{n\times n}$ be a matrix, and define a function $f:\mathbb{R}^n \rightarrow \mathbb{R}^n$ by $f(\mathbf{v}) = A\mathbf{v}$. (These types of functions were introduced in section 1.6; they're called matrix transformations.)
- If $A$ is invertible, show that $f$ is an isomorphism. (Remember there are 4 things to show.)
- If $A$ is not invertible, show that $f$ is not an isomorphism. (Note, $f$ is not an isomorphism as soon as one of the four properties fails.)
|
|
[04.13.16] - Wednesday
|
|
Sections covered: 4.8 (almost finished)
|
Reading for next time: Section 4.9. Focus on the following:
- Intro through Example 1
|
To discuss next time: let's make a review sheet for the midterm. The exam will cover up through section 4.8, excluding section 4.7. Same directions as before, but with a new link...
- Please construct one question of the form "provide a specific example which satisfies the given description, or if no such example exists, briefly explain why not" and add it to our review sheet here
https://www.sharelatex.com/project/570e88cfe18718921bb52d30
The review sheet already contains some questions that you can use as an example.
Make sure to
- put your initials next to your questions, and
- put an answer in the "Answers" section of the document.
- Repeat with a T/F question.
- Make sure to write down your questions and answers on paper too, so you are prepared to present them in class.
|
|
[04.15.16] - Friday
Good job on the review sheet! Here's (a slightly edited version of) what you made:
Exam2ReviewQuestions.pdf
|
|
Sections covered: 4.7, 4.9 (started)
|
|
Reading for next time: None. Focus on studying!
|
To discuss next time:
- Give an example of a $3 \times 4$ matrix for which the row space has dimension 2. (You can make your example as simple as you like.)
- What is the dimension of the column space of your example?
- Is it possible to find a $3 \times 4$ matrix for which the row space has dimension 4?
- Is it possible to find a $3 \times 4$ matrix for which the column space has dimension 4?
|
| Week 12 |
|---|
|
[04.18.16] - Monday
|
|
Sections covered: 4.9 (finished), 6.1 (started)
|
Reading for next time: Section 6.1. Focus on the following:
- Definition 6.1
- Examples 1, 4
- Theorem 6.2 as well as the paragraphs immediately before and immediately after it.
|
|
To discuss next time: just focus on studying. Good Luck!
|
|
[04.20.16] - Wednesday
|
|
Sections covered: 6.1 (finished)
|
Reading for next time: Section 6.2. Focus on the following:
- Definitions 6.2, 6.3, 6.4
- Examples 2, 3, 5
- Examples 4, 6
|
To discuss next time: Let $L:P_3 \rightarrow P_2$ be defined by $L(p(t)) = \frac{d}{dt}(p(t))$
- Is $L$ one-to-one?
- What polynomials (from $P_3$) are in $\operatorname{ker}(L)$?
- Is $L$ onto?
- What polynomials (from $P_2$) are in $\operatorname{range}(L)$?
|
|
[04.22.16] - Friday
|
|
Sections covered: 6.2 (started)
|
Reading for next time: Section 6.2. Focus on the following:
- Theorem 6.6 (this should remind you of the Rank-Nullity Theorem)
- Examples 9 and 10
|
To discuss next time: Let $L:M_{3\times 3} \rightarrow \mathbb{R}$ be defined by $L(A) = \operatorname{tr}(A)$. (Remember that $\operatorname{tr}(A)$ denotes the trace of $A$.)
- Explain why $L$ is a linear transformation. (Make use of the properties of trace.)
- Describe $\operatorname{range}(L)$. Is $L$ onto? What is $\dim(\operatorname{range}(L))$?
- Describe $\operatorname{ker}(L)$. (Hint: we've talked about the matrices in $\operatorname{ker}(L)$ many times before.) Is $L$ one-to-one? Use Theorem 6.6 to quickly find $\dim(\operatorname{ker}(L))$.
|
| Week 13 |
|---|
|
[04.25.16] - Monday
|
|
Sections covered: 6.2 (almost finished)
|
Reading for next time: Section 6.3. Focus on the following:
- Introduction
- Example 1
|
To discuss next time:
- We have seen that "taking the derivative" is a linear transformation. That is, for every positive $n$, the function $L:P_n\rightarrow P_n$ defined by $L(p(t)) = p'(t)$ is a linear transformation. Section 6.2 is about finding a way to view $L$ as a matrix transformation.
- Notice that I wrote $L:P_n\rightarrow P_n$ instead of $L:P_n\rightarrow P_{n-1}$. Think about how that choice affects the following questions. What else might that choice affect, e.g. onto, one-to-one,...?
- Let $p(t) =a + bt + ct^2$. Compare $p'(t)$ with $\begin{bmatrix}0 & 1 & 0\\0 & 0 & 2\\0 & 0 & 0 \end{bmatrix}\begin{bmatrix}a\\b\\c \end{bmatrix}$.
- Let $p(t) =a + bt + ct^2 + dt^3$. Compare $p'(t)$ with $\begin{bmatrix}0 & 1 & 0 & 0\\0 & 0 & 2 & 0\\0 & 0 & 0 & 3\\0 & 0 & 0 & 0\end{bmatrix}\begin{bmatrix}a\\b\\c\\d \end{bmatrix}$.
- Can you generalize the above situation? What matrix would you use to compute the derivative of $p(t)= a_0 + a_1t + a_2t^2 + \cdots a_nt^n$? Why?
|
|
[04.27.16] - Wednesday
|
|
Sections covered: 6.2 (finished), 6.3
|
Reading for next time: Section 7.1. Focus on the following:
- Intro through Definition 7.1
|
To discuss next time:
- Let $L:\mathbb{R}^2\rightarrow\mathbb{R}^2$ be defined by $L\left(\begin{bmatrix}x\\y\end{bmatrix}\right) = \begin{bmatrix}y\\x\end{bmatrix}$
- Find all $\mathbf{v} \in \mathbb{R}^2$ such that $L(\mathbf{v}) = \mathbf{v}$. Can you also explain this geometrically (by thinking about $L$ geometrically)?
- Find all $\mathbf{v} \in \mathbb{R}^2$ such that $L(\mathbf{v}) = -\mathbf{v}$. Can you explain this geometrically as well?
- Find all $\mathbf{v} \in \mathbb{R}^2$ such that $L(\mathbf{v}) = 2\mathbf{v}$. Can you explain this geometrically?
|
|
[04.29.16] - Friday
|
|
Sections covered: 7.1 (started)
|
Reading for next time: Section 7.1. Focus on the following:
- The definitions of eigenvalue and eigenvector of a matrix in the middle of page 442
- Definition 7.2 (this is really important!)
- Example 11 and 12
|
To discuss next time:
- Find the characteristic polynomial of $\displaystyle A=\begin{bmatrix}2 & 7\\7 &2\end{bmatrix}$. Please write the polynomial in factored form.
- Find the characteristic polynomial of $\displaystyle A=\begin{bmatrix}1 & 0 & 0\\3 & 2 & 0\\ 0 & 0 & 1\end{bmatrix}$. Please write the polynomial in factored form.
- If $a_{ij}$ are arbitrary real numbers, find the characteristic polynomial of $\displaystyle A=\begin{bmatrix}a_{11} & 0 & 0\\a_{21} & a_{22} & 0\\ a_{31} & a_{32} & a_{33}\end{bmatrix}$. Please write the polynomial in factored form.
- If $A = [a_{ij}]$ is an arbitrary $n\times n$ lower triangular matrix, find the characteristic polynomial, in factored form, of $A$.
|
| Week 14 |
|---|
|
[05.02.16] - Monday
|
|
Sections covered: 7.1 (continued)
|
Reading for next time: Page 410. Focus on the following:
- The definition of similar matrices on page 410
|
To discuss next time:
- "Similar matrices are similar." Let $A,B \in M_{n\times n}$, and assume $B$ is similar to $A$, i.e. $B = P^{-1}AP$ for some invertible matrix $P$.
- Explain why $\operatorname{Tr}(A) = \operatorname{Tr}(B)$? Hint: use properties of the trace.
- Explain why $\det(A) = \det(B)$? Hint: use properties of the determinant.
- Can you think of other things that may be the same for similar matrices?
- Explain why $B^k = P^{-1}A^kP$ for any positive integer $k$. Hint: to see what's going on, start with $k=2$, and try to simplify $B^2 = (P^{-1}AP)^2$
|
|
[05.04.16] - Wednesday
|
|
Sections covered: 7.1 (finished), 7.2 (started)
|
Reading for next time: Section 7.2. Focus on the following:
- Theorem 7.4, and the remark following Theorem 7.4
- The discussion between Examples 3 and 4 (this, together with Theorem 7.4, is what I presented as the Diagonalization Theorem in class)
- Theorem 7.5
- Examples 2-6
|
To discuss next time: Consider the following martices: \[A=\begin{bmatrix}1 & 0 & 0\\3 & 2 & 0\\ 0 & 0 & 1\end{bmatrix}\quad\quad B = \begin{bmatrix}1 & 0 & 0\\3 & 1 & 0\\ 0 & 0 & 2\end{bmatrix} \]
Note that both matrices have the same characteristic polynomial, which is \[p(\lambda) = (\lambda-1)^2(\lambda - 2).\]
- Find a basis for $E_1(A)$, i.e. the eigenspace of A associated to $\lambda=1$.
- Find a basis for $E_2(A)$, i.e. the eigenspace of A associated to $\lambda=2$.
- Show that when your basis for $E_1(A)$ is combined with your basis for $E_2(A)$, you get a basis for $\mathbb{R}^3$, and explain why this shows that $A$ is diagonalizable. (Hint: to see why $A$ is diagonalizable, use Theorem 7.4, i.e. the Diagonalization Theorem.)
- Find a basis for $E_1(B)$ and a basis for $E_2(B)$.
- Explain why $B$ is NOT diagonalizable. (Hint: use the Diagonalization Theorem; remember it is an if and only if statement.)
|
|
[05.06.16] - Friday
We had a great last day of presentations! Thanks to everyone who shared their eigenknowledge.
|
|
Sections covered: 7.2 (finished)
|
|
Reading for next time: Finish reading Section 7.2, and start reviewing for the final.
|
|
To discuss next time: Let's make a review sheet for the final exam. Focus on the material since the last exam, i.e. sections 4.7, 4.9, 6.1, 6.2, 6.3, 7.1, 7.2, but don't forget the "old" stuff. Same directions as before, but with a new link...
https://www.sharelatex.com/project/572cecd7fddf965455c829ca
|
| Week 15 |
|---|
|
[05.09.16] - Monday
Done!! Thanks for a great semester!
|