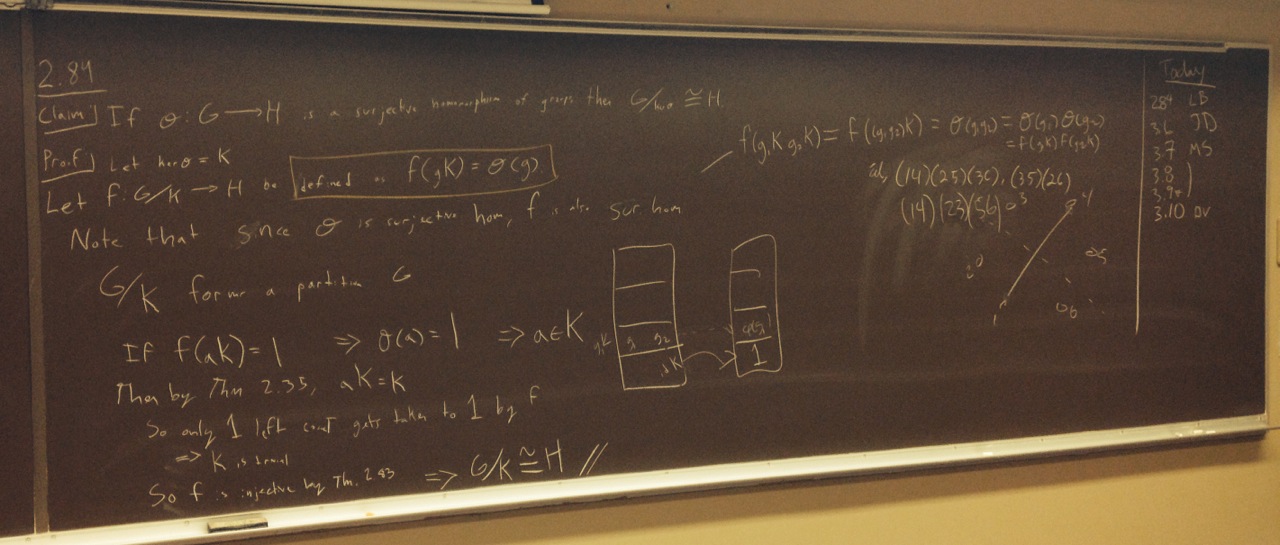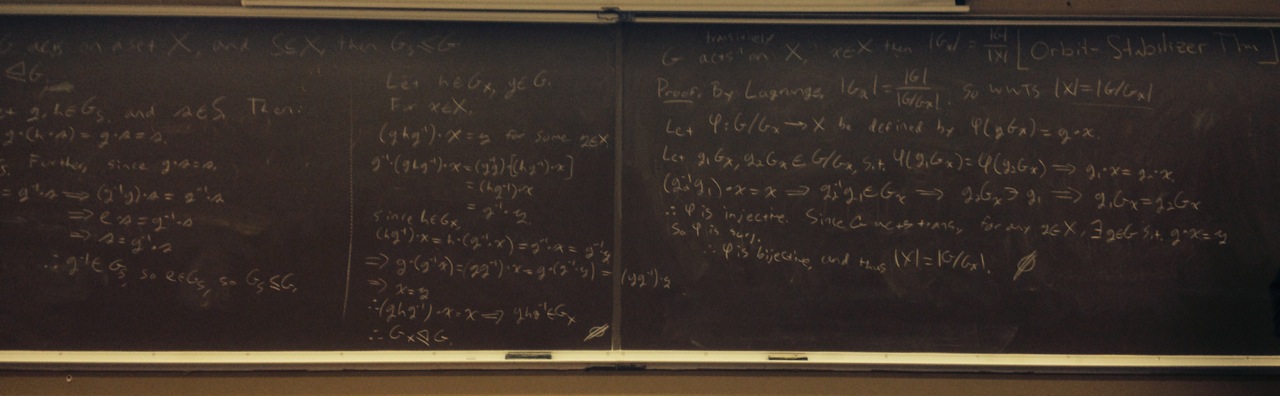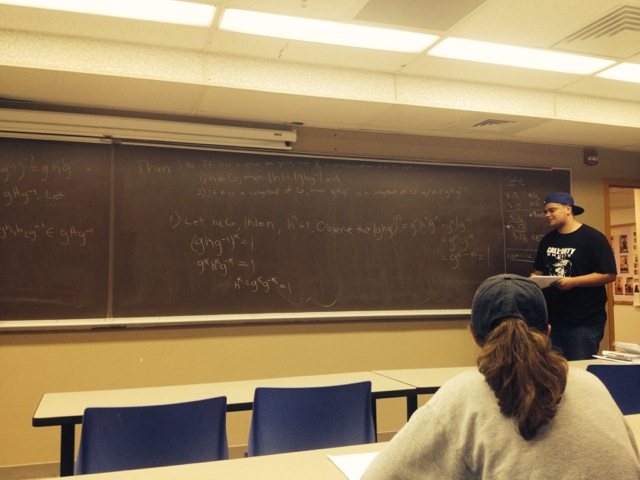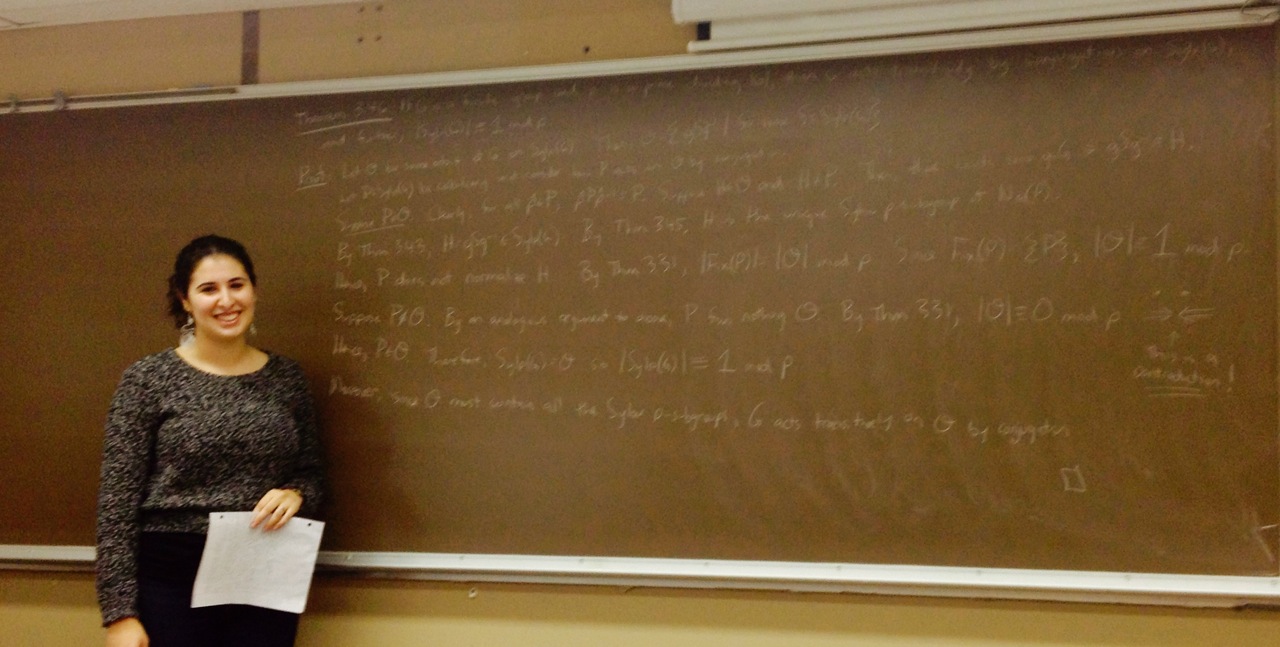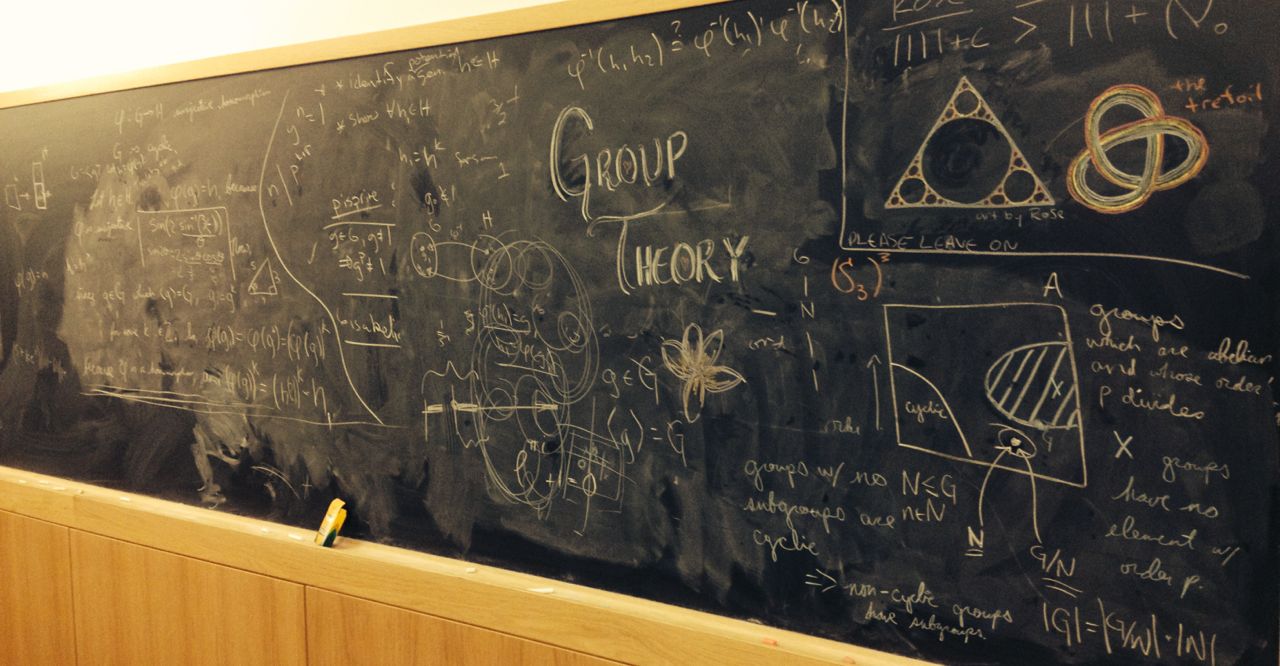
An Introduction to the Theory of Groups (Math 437 section 01)

Class times: 10:30AM - 11:45AM, TR (JHSN 222)
Office Hours: 2:30PM - 4:30PM, MWF; or by appointment

Most of the general information about the course can be found in the syllabus. Student grades will be maintained on Blackboard.

Course Notes and More

1 - Examples
[updated on 09.10.14]

2 - Abstract Groups
[updated on 10.14.14]

3 - Group Actions
[updated on 11.18.14]

Project Template
[updated on 11.11.14]

Project Schedule

Here is the schedule for project presentations along with the tentative titles. They look great!

12.04.14	12.08.14	12.11.14	12.17.14
Transfer Theory (DV)	Free groups (SC)	Group representations with applications in physics (JD)	The isomorphism theorems (EM)
	Thompson's groups (RBZ)	An Introductions to multiply transitive groups (MS)	Nilpotent groups (MG)
		The classification of the finite simple groups (AOE)	Burnside's problem (LB)
			Finite Coxeter groups (AM)

Course Log

Jump to week: 1 -- 2 -- 3 -- 4 -- 5 -- 6 -- 7 -- 8 -- 9 -- 10 -- 11 -- 12 -- 13 -- 14 -- 15 and beyond

Week 1

[08.28.14] - First day!

Could not have hoped for a better first class. The brave DV and MG rocked the first two presentations of the course, both exposing some subtle points - big thanks! The rest of the class was very involved and vocal (yes!); a big thanks to MS for taking the lead on this. Psyched for Tuesday!

Problems/theorems covered: Th. 1.4 (DV-JW), Pr. 1.5 (MG)

Goal for next time: 1.7 - 1.17; we will skip Problem 1.6, but please look it over (or just do it)

Week 2

[09.02.14]

Another great day! Definitely starting things off right. Had nice presentations from ZY and RBZ that generated some good dialog. MS had a great comment about finding the inverse of a product of cycles that are not necessarily disjoint. DV crushed the rather challenging Theorem 1.15. The presentation was quite nice with a fantastic balance of writing an talking. SC had a great comment about a different way to count the number of elements of order 2 with a given cycle type. In fact, there were good comments all around.

Problems/theorems covered: Pr. 1.7 (ZY), Th. 1.14 (RBZ), Th. 1.15 (DV)

Goal for next time: 1.16, 1.17, 1.18 - 1.30; the red problems were collected last time but still needed to be presented

[09.04.14]

Nice presentations from MS and SC and great dialog. Had a very brief chat about whether or not the lcm of a set of integers divides every common multiple (as a possible clean end game to 1.17). Did you all sort it out? SC gave a very general argument to a specific problem that we agreed should generalize to show that every cyclic group is abelian. We ended with a nice group discussion about Th. 1.26 led by AM. Well done all around. Well, except for me since I had to split my attention with grading...sorry!!

Problems/theorems covered: Th. 1.17 (MS), Pr. 1.22 (SC), discussion about Th. 1.26 (AM)

Due next time: 1.27 - 1.33

Presentation goal for next time: 1.16, 1.26, 1.30, 1.32, 1.33

- Dihedral and cyclic groups are taking over CJ! -

Week 3

[09.09.14]

LB started it off with a very nice and concise proof of Th. 1.16. There was focus on the action of Sym(X) on X over abstract group theory which seemed to streamline things. AOE took us through Th. 1.29 with a clear and extremely well-written proof. The proof utilized the the fact that C_n acts regularly, i.e. transitively and freely, on the relevant graph. We are starting to see the value of studying groups via actions. Finally, EM patiently guided us through Pr. 1.30. This generated great discussion about different ways to count the elements that generate C_n that ended with a rather insightful comment by DV. Great job all around!

Problems/theorems covered: Th. 1.16 (LB), Th. 1.29 (AOE), Pr. 1.30 (EM)

Due next time: 1.34 - 1.37

Presentation goal for next time: 1.26 (AM?), 1.32 (AA?), 1.35, 1.37

[09.11.14]

Great day! So much to record... Started with a brief discussion about free actions. Then AA took us through a very nice presentation of the fact that C_∞ is cyclic. AM followed it up with a clear and concise proof that cyclic groups are abelian. RBZ delivered a very clean presentation, while nicely fielding several questions, of Th. 1.36 showing that the dihedral groups (including the infinite one) are nonabelian (except for D₂, of course). This led to a brief discussion about notation for elements in D_∞. Then MS asked a great question that evolved into a discussion as to what the centralizer is, in D_∞, of the element that translates every vertex by 1, and after about 30 seconds, AM crushed it! We concluded with JD's proof of Th. 37. His presentation went above and beyond what was necessary and hinted at a more general theorem, which was ultimately vocalized by DV. Fantastic job!

Problems/theorems covered: Th. 1.32 (AA), Th. 1.35 (AM), Th. 1.36 (RBZ), Th. 1.37 (JD)

Due next time: 1.38 - 2.3 (LaTeX: two of 1.32, 1.35, 1.37)

Presentation goal for next time: 1.41, 1.42, 1.43, 1.44, 2.2, 2.3

Week 4

[09.16.14]

JD started it off with a very nice, albiet partial, proof of Th. 1.41. The "generic case" was treated very efficiently, but after questions by RBZ and AM, we realized that there were a number of other cases that need to be addressed. We put the problem on hold, and JD will present the end game next time. We then paused for a brief discussion about transitivity. The main point was that transitivity follows from simply knowing that one element can be mapped to any other by some element of the group. Next, MG gave a great constructive and to-the-point proof of Th. 1.42. MS then guided us through Th. 1.43. The example showing that commutativity fails for GL_n when n is at least 2 was quite general, but we noticed that it needed a slight bit of doctoring to ensure that the matrices involved were actually in GL_n. In the end, the solution nicely illustrated how treating the special case of n=2 easily extended to larger n. Finally, SC and EM brought it home with great "by-the-book" proofs of Th. 1.43 and Th. 2.3. Excellent day - as usual!

Problems/theorems covered: Th. 1.42 (MG), Th. 1.43 (MS), Th. 1.43 (SC), Th. 2.3 (EM)

Due next time: 2.4 - 2.13

Presentation goal for next time: 1.41 (JD), 2.8, 2.9 (time permitting), 2.11, 2.13

[09.18.14]

Fantastic presentations by JD, DV (x 2), and LB. Everything was right on, so there's not much to say...except, nice job! We finished presentations a bit early and took the opportunity to raise some questions...

We know that groups of exponent 2 are abelian. What, if anything, can be said about exponent 3?
To what degree is the following table complete? Are all groups on the table honestly different?

Order 1 2 3 4 5 6 7 8

trivial group C₂ or Z₂ C₃ or Z₃ C₄ or Z₄ C₅ or Z₅ C₆ or Z₆ C₇ or Z₇ C₈ or Z₈

Z₂ x Z₂ S₃ D₈

Z₂xZ₃ Q₈

Problems/theorems covered: Th. 1.41 (JD), Th. 2.8 (DV), Th. 2.13 (LB), Th. 2.11 (revised version) (DV)

Due next time: 2.13 - 2.24; LaTeX: two of 1.41, 1.42, 1.43, 1.44, 2.8

Presentation goal for next time: 2.14, 2.16, 2.17, 2.21, 2.23, 2.24

Week 5

[09.23.14]

Fun day! Started off by discussing the possibility of holding next Tuesday's class at the Cider Mill over cider and doughnuts... We'll see; perhaps the Cider Mill will have to come to us. Moving on, we saw five very solid presentations. AOE took us through the proof that the powers of any group element g form a subgroup with exactly order of g many elements. What seemed to be such an obvious fact in fact had a couple of nontrivial details to address. The problems presented by SC and MG exposed us to the lattice of subgroups for of a group. RBZ identified some interesting subgroups of S₄, and we had a little discussion about others. RBZ gave the canonical example of a proper nonabelian subgroup of S₄, namely S₃. DV mentioned one that he found which we will see is a so-called Sylow 2-subgroup of S₄ and is morally the same as the Dihedral group of order 8. DV then brought it home with a proof of the fact that every subgroup of a cyclic group is cyclic. This was not easy! DV's proof also seemed to hint at a way to streamline things from the start. We will see. Great job!

Problems/theorems covered: Th. 2.14 (AOE), Pr. 2.16 (SC), Pr. 2.17 (RBZ), Pr. 2.21 (MG), Th. 2.23 (DV)

Due next time: 2.25 - 2.31; also read 2.32-2.33

Presentation goal for next time: 2.24 (JD), 2.26, 2.27, 2.29, 2.31

[09.25.14]

Solid day. Did some nice group theory, and in addition to covering 2.24 - 2.31, we also answered (in the negative) the following question of DV.

If g and h are elements of a (not necessarily abelian) group, can we conclude that the order of gh divides the least common multiple of the orders of g and h?

Please keep up the side questions!

Problems/theorems covered: Th. 2.24 (JD), Th. 2.27 (EM), Pr. 2.29 (SC), Pr. 2.31 (MS)

Due next time: 2.32 - 2.44 but you do not need to prove Th. 2.33

Presentation goal for next time: 2.34, 2.35, 2.38, 2.41, 2.42, 2.43

Week 6

[09.30.14]

Celebrated the beautiful autumn weather with some Cider Mill cider, doughnuts, and apples as well as the crushing of Lagrange's Theorem. We started class by realizing that we had a bit of confusion about the notation surrounding Pr. 2.34, which is certainly to be expected. We chatted a bit about additive notation for abelian groups and what Pr. 2.34 was really talking about. The problem was ultimately pushed to the next meeting so that everyone could take another shot at it. Thanks to AOE and MS for guiding us through the problem. Next, RBZ took down Th. 2.35, taking care of much of the setup for Lagrange's Theorem. The presentation of the next theorem, showing that G/H partitions G, was pushed to next time, and we moved on to Lagrange's Theorem. AOE had the honor and gave a very clear and concise proof that certainly did the theorem justice. Finally, LB and AM made extremely short work of the first two applications of Lagrange's Theorem; both presentations were nothing short of perfect and by-the-book. Great job all around! Happy autumn!

Problems/theorems covered: Pr. 2.34 (MS-AOE), Th. 2.35 (RBZ), Th. 2.41 (AOE), Th. 2.42 (LB), Th. 2.43 (AM)

Due next time: 2.44 - 2.54

Presentation goal for next time: 2.38 (AA?), 2.46, 2.47, 2.51, 2.52, 2.54

[10.02.14]

Started class with AA taking us through the proof, complete with a nice picture, that the cosets of a subgroup partition the group. JD followed it up with an extremely efficient proof, essential by drawing the right picture, that subgroups of index 2 are necessarily normal. We then moved to quotient groups. We started by discussing Th. 2.47 but got side-tracked by a question about coset arithmetic:

if N is a normal subgroup of G, is it true that gaN = agN for all a and g in G?

We'll be prepared to discuss this next time and finish Th. 2.47. Next, EM showed us that quotients of cyclic groups are again cyclic, and SC illustrated that simply having a cyclic quotient does NOT imply the original group is cyclic, even when the normal subgroup is cyclic. The example of SC came from Q₈, and we also discussed examples from S₃ and D₄. Finally, DV proved that having a cyclic quotient DOES imply the original group is abelian provided the normal subgroup is central. Very nice day!

Problems/theorems covered: Th. 2.38 (AA), Th. 2.46 (JD), Th. 2.51 (EM), Pr. 2.52 (SC), Th. 2.54 (DV)

Due next time: 2.55 - 2.63 (LaTeX: two of 2.35, 2.38, 2.41, 2.42, 2.43, 2.46, 2.51, 2.54)

Presentation goal for next time: Th. 2.47 (MS?), Th. 2.57, Th. 2.60, Th. 2.61, Th. 2.62

Week 7

[10.07.14]

Good day with hard problems. MS started it off by wrapping up 2.47, and clarifying the question from last time. We have the feeling that the answer to the question is NO, but we haven't yet come up with an example. We then moved on to some hard problems involving quotient groups as well as the new notion of p-divisibility. EM, MG and RBZ did great! We are starting to see how to work with and exploit quotient groups, but it certainly takes practice. Ultimately, we pushed 2.62 back to the next meeting so that we could have more time to meditate on it. It's hard. Thursday's going to be fun!

Problems/theorems covered:Th. 2.47 (MS), Th. 2.57 (EM), Th. 2.60 (MG), Th. 2.61 (RBZ)

Due next time: 2.64 - 2.71

Presentation goal for next time: Th. 2.62, Th. 2.66, Th. 2.68, Th. 2.70

[10.09.14]

Great day, with the pictures to prove it! DV started it off with a proof of the theorem that every finite abelian group of order divisible by a prime p has an element of order p. The theorem was HARD, but we learned a lot about working with minimal counterexamples and exploiting subgroups and quotient groups. We then had a discussion about whether or not we could improve the theorem. JD suggested that perhaps G need only have a central subgroup, and we are now working on this as Th. 2.63.1. Very nice! We also voted on if the theorem should hold for all finite groups; the tally was Huzzah: 5, Nay: 6. Next JD and AOE got our study of homomorphisms and isomorphisms started with two very clean and spot-on presentations. Great job!!

Problems/theorems covered: Th. 2.62 (DV), Th. 2.66 (JD), Th. 2.68 (AOE)

Due next time: 2.63.1, 2.72 - 2.77 (LaTeX: two of 2.57, 2.60, 2.61, 2.62, 2.66)

Presentation goal for next time: Th. 2.70 (AM), Th. 2.63.1, Th. 2.72, Th. 2.73, Pr. 2.74, Pr. 2.76, Pr. 2.77

- DV proving the decidedly hard fact that every finite abelian group of order divisible by a prime p has an element of order p...Victory! -

- JD and AOE crushing our first theorems about isomorphisms. -

Week 8

[10.14.14]

Interesting day. It started with AOE sent to the board on a suicide mission. The "old" Th 2.63.1 (it has since been updated) requested a proof of the fact that if a finite group with nontrivial center has order divisible by a prime p then the group has an element of order p. As we investigated the end game, we realized that the argument wasn't going to work (DV was all over this!), and more importantly, we didn't know how to fix it. The presentation given by AOE was extremely clear and illustrated perfectly what we want to do, though we couldn't yet do it. I confessed that I hadn't fully thought out the theorem when assigning it. We definitely need more tools to determine if the theorem as stated is even true. That said, the discussion surrounding the situation made it quite clear that the class has matured A LOT as group theorists. Further, AOE's methods were more than adequate to prove the following nontrivial generalization of Th. 2.62.

Theorem: Let G be a finite group with nontrivial center AND assume that G/Z(G) is abelian. If p is a prime dividing |G|, then G has an element of order p.

We finished off class with three very well-done and spot-on presentations by AM, LB, and DV that, among other things, illustrated how comfortable we are becoming working with homomorphisms. Well done everyone...well, I could have done a bit better ☺

Problems/theorems covered: Th. 2.63.1 (AOE), Th. 2.70 (AM), Th. 2.72 (LB), Th. 2.73 (DV)

Due next time: 2.78 - 2.86, 3.1 - 3.6 (LaTeX: two of 2.70, 2.72, 2.73)

Presentation goal for next time: Pr. 2.74 (SC), Pr. 2.76 (MG), Pr. 2.79, Th. 2.81, Th. 2.83, Pr. 2.86, Pr 3.6

[10.16.14]

Fall Break! Enjoy!

Week 9

[10.21.14]

Good, albeit low-energy, day. Seems like the semester is starting to take it toll, but maybe it's just the change of seasons... We covered several more problems about homomorphisms today. SC started it off by showing that the subgroups nZ of Z are all isomorphic to Z itself. MG gave a great presentation about the additive group of the real numbers R⁺ and the multiplicative group of nonzero real numbers R^x. MG showed that R⁺ is not isomorphic to R^x by looking at elements of order 2 and also showed that R⁺ is isomorphic to the subgroup of R^x consisting of the positive elements via exponentiation. AM proved that the image and kernel of a homomorphism are subgroups and that the later is normal. This also took us on a discussion of other conditions for normality, namely that N = gNg^-1. Finally, DV showed that SL_n is normal in GL_n by showing that it is the kernel of the determinant map and then described, very nicely, the quotient GL_n/SL_n. Well done everyone...but get rested up for Thursday!

Problems/theorems covered: Pr. 2.74 (SC), Pr. 2.76 (MG), Th. 2.81 (AM), Th. 2.86 (DV)

Due next time: 3.6 - 3.10

Presentation goal for next time: Th. 2.84, Th. 3.6, Pr. 3.7, Pr. 3.8, Pr. 3.9, Th. 3.10

[10.23.14]

Energy was a bit higher today, and good things happened. LB crushed the First Isomorphism Theorem, complete with a great picture, which we followed with a brief discussion about functions being well-defined. JD took down Th. 3.6 with a picture that was so clear that we hardly need to see the actual proof. MS walked us through some questions about how D₆ (and C₆) act on the three diagonals of the regular (directed) hexagon. Super clear! We talked about the image of this permutation representation using a combination of concrete calculations and general First Isomorphism Theorem calculations. Finally, DV presented Th. 3.10. After a very nice presentation, DV requested to talk about an "observation" that he made and then proceded to prove the Orbit-Stabilizer Theorem (which is coming soon)...WOW!...I mean, WOW!!!

- First Isomorphism Theorem, courtesy of LB -

- Th. 3.10 and DV's "observation" -

Problems/theorems covered: Th. 2.84 (LB), Th. 3.6 (JD), Pr. 3.7 (MS), Pr. 3.8 (MS), Th. 3.10 (DV)

Due next time: 3.11 - 3.18 (LaTeX: two of 2.81, 2.83, 2.84, 3.6, 3.10)

Presentation goal for next time: Th. 3.13, Th. 3.14, Th. 3.16, Th. 3.17, Pr. 3.18

Week 10

[10.28.14]

Started off with some important applications of groups acting on coset spaces to nonsimplicity. The proofs invoked the associated permutation representation, and MG and DZ did an excellent job of guiding us through the details. And yes, he turned to the right! We then moved on to groups acting on themselves by conjugation. In our quest for the Sylow Theorems, this was the beginning of the end, and RBZ and the Boss got us started off right.

- DZ and MG showing that groups with "big" proper subgroups are not simple. -

- RBZ and the Boss proving theorems about conjugation. -

Problems/theorems covered: Th. 3.13 (MG), Th. 3.14 (AOE), Th. 3.16 (EM), Pr. 3.18 (RBZ)

Due next time: 3.19 - 3.25

Presentation goal for next time: Th. 3.19, Th. 3.21, Pr. 3.23, Pr. 3.24, Th. 3.25

[10.30.14]

Today was exceptionally exceptional! I had just sat down to watch the first presentation when I looked up to see myself and Topaz walking in the door with cider and doughnuts. As my other self conducted class, I just watched in awe at all of my ridiculous mannerisms. It was hilarious, and I enjoyed every minute of it. After plenty of cider, doughnuts, and laughs, AA got us started with a very important theorem on how conjugation works in S_n. We then jumped to Th. 3.25, so DV could use AA's theorem to connected conjugacy classes and cycle type in S_n. Next, RBZ gave a very nice and concise proof of the fact that the orbits partition the set being acted on, and AM wrapped things up with a presentation of conjugacy classes of elements and conjugacy classes of subgroups in S₃. We realized that many of us had some confusion about the latter, but it seemed like we sorted things out quickly. Great day. Big thanks to AOE and SC for the early birthday present!

- Other-Josh and Other-Topaz take over class! AA taking down a theorem about conjugation in S_n. -

Problems/theorems covered: Th. 3.17 (AA), Th. 3.21 (RBZ), Pr. 3.23 (AM), Th. 3.25 (DV)

Due next time: 3.26 - 3.33 (LaTeX: none this week)

Presentation goal for next time: Pr. 3.24, Th. 3.26, Th. 3.30, Th. 3.31, Th. 3.32, Th. 3.33

Week 11

[11.04.14]

Started the day with a very clean and concise proof by SC of the fact that Z(S_n) = 1 whenever n > 2. RBZ then took us through a very important result for making computations with group actions, namely that |X| = |Fix(G)|+|G : G_x₁| + ... + |G : G_{x_n}|. The proof was spot on and super clear, thanks in part to an excellent illustration. JD and DV then presented two applications of this result to groups of prime-power order. JD's was about fixed points for an arbitrary action of such a group, and DV applied this to show that the center of a group of prime-power order is nontrivial. This final result also gave the opportunity to mention nilpotent groups, which we will hear more about later. Great day - Thanks!

- RBZ -

Problems/theorems covered: Th. 3.26 (SC), Th. 3.30 (RBZ), Th. 3.31 (JD), Th. 3.32 (DV)

Due next time: 3.34 - 3.37

Presentation goal for next time: Th. 3.33, Pr. 3.34, Th. 3.35, Th. 3.36 (AOE), Pr. 3.37

[11.06.14]

Began the the day with The Boss showing us that groups of order p² are abelian. In light of our past efforts, the theorem fell with just a handful of lines of proof; very nice. MG then gave a great presentation of 3.35 and with it, kicked down the door to Cauchy! AOE (DZ?) had the honor of taking us in and proving a theorem that was a long time in the making. The proof was fantastic and very colorful! And then it happened...he turned to the left and time stopped as we all bore witness to...MAGNUM! Absolutely breathtaking. Much to my surprise, I was able to catch it on camera. After collecting ourselves, we had a discussion about generalizing (and not being able to generalize) Cauchy's Theorem. Several different conjectures and questions were raised. Here are some concrete versions of them. We answered the third in the negative. What about the first two?

Question: Let G be a finite group. If 6 divides |G|, must G have an element of order 6?
Question: Let G be a finite abelian group. If 6 divides |G|, must G have an element of order 6?
Question: Let G be a finite group. If 4 divides |G|, must G have an element of order 4?

We also rephrased Cauchy's Theorem in terms of subgroups and discussed generalizing things that way, which naturally led to mentioning Sylow.

- Cauchy and Magnum! -

Problems/theorems covered: Th. 3.33 (#BOSS), Th. 3.35 (MG), Th. 3.36 (AOE)

Due next time: 3.19.1 - 3.19.2, 3.38 - 3.43 (LaTeX: two or three of 3.13, 3.14, 3.16, 3.17, 3.19, 3.21, 3.25, 3.26, 3.28 3.30 - 3.33)

Presentation goal for next time: Th. 3.19.2, Th. 3.38, Pr. 3.41, Pr. 3.42, Th. 3.43

Week 12

[11.11.14]

Got working on Sylow subgroups today. Started with LB using Cauchy to show that finite p-groups are exactly the groups of prime-power order. We then found Sylow subgroups of S₄ and S₅. The problems were about Sylow 5-subgroups of S₅ and Sylow 2-subgroups of S₄, but we ended up discussing the other primes too. Then we wrapped up with AOE proving that every group acts on its Sylow p-subgroups by conjugation. Very nice day but, sadly, no pics. Getting close to serving up Sylow's Theorems.

Problems/theorems covered: Th. 3.38 (LB), Pr. 3.41 (MS), Pr. 3.42 (DV), Th. 3.43 (AOE)

Due next time: 3.44 - 3.45

Presentation goal for next time: Th. 3.19.2, Th. 3.44, Th. 3.45

[11.13.14]

Short day of presentations as MS and DV crushed the final two lemmas needed for Sylow's Theorems. We killed the remaining time with a discussion of various topics that began with addressing the question "why do we care about Sylow subgroups?" This started with an analogy to factoring numbers and led to the fact that after selecting one Sylow p-subgroup for each relevant p we obtain a collection of subgroups that pairwise intersect trivially and generate the group. The analogy with factoring numbers was reinforced upon specializing our observation to abelian groups, and this also gave an excellent opportunity to mention nilpotent groups again. To tidy things up we then (finally!!) defined direct products of groups. This then morphed into a discussion of groups of small order, and after we continued to revisit the notion of "factoring" groups, we ended with the following questions:

Question: What is an example of a living, breathing nonabelian simple group?
Question: What is the order of the smallest nonabelian simple group?

- MS showing us the light! -

Problems/theorems covered: Th. 3.44 (MS), Th. 3.45 (DV)

Due next time: 3.46 - 3.47 (LaTeX: two of 3.35, 3.36, 3.38, 3.43, 3.44, 3.45)

Presentation goal for next time: Th. 3.19.2 (SC), Th. 3.46, Th. 3.47

Week 13

[11.18.14]

Glorious day! Sylow's Theorems! We all put in a lot of energy to make it here, and the presentations today most certainly did our effort justice. Very, very well done! We had a little talk about applications of Sylow's Theorems, and we will discuss this more next time as we take a crack at determining the order of the smallest nonabelian simple group (see the worksheet handed out today). Also, there are only two more theorems in the course notes, and then we transition to projects. The list of project topics is impressive and will be posted here soon.

- RBZ and MG making Sylow (and me) proud. -

Problems/theorems covered: Th. 3.19.2 (SC), Th. 3.46 (RBZ), Th. 3.47 (MG)

Due next time: 3.48 - 3.50

Presentation goal for next time: Th. 3.49, Th. 3.50

[11.20.14]

Finished up the course notes today, just in time for break. The atmosphere was decidedly light as the proofs were paired with music! SC started things off, seeking redemption, and delivered a fantastic proof of Th 3.49, perfectly fused with the Star Wars Cantina Theme. We loved it! We then paused to do a little analysis of groups of small order. Using Th 3.49 and several of our previous theorems, we filled in a good portion of our small groups worksheet. Ultimately it was a nice lead-in to our final theorem, which was about groups whose order is a product of three distinct primes. There was a battle for the glory of presenting the final proof, and we decided that the appropriate course of action was to let JD and MS go at it simultaneously - showdown style. SC cued up the theme from The Good, the Bad and the Ugly, and the rest is history. Going to have to call it a draw, but we all won today ☺

- Crushed it! -

Problems/theorems covered: Th. 3.49 (SC), Th. 3.50 (JD-MS)

Due next time: Please edit the project template to include (a preliminary version of) each of the following, and EMAIL me the resulting pdf file.

Title
Section names (the first will be "Introduction," but you should have at least one more section)
The first 1 or 2 paragraphs of your introduction
All of the definitions that you will need, located in the appropriate sections
The statements of at least 2 of the theorems (or lemmas, propositions, etc.) that you plan to discuss, even if you won't prove them all

In class next time: small groups - bring your worksheets

- RBZ and AOE working extra hard... -

Week 14

[12.02.14]

Spent the day working through more of the small groups worksheet, and found that there are no nonabelian simple groups of order less than 60. We used a combination of Sylow theory, and actions on cosets of subgroups of small index. We have some ideas for 60, perhaps a variant we used for counting elements in groups whose order is a product of three distinct primes, but we will see... Presentations start Thursday!! Very excited! The schedule is posted at the top of the page.

Next time: Transfer Theory (DV)

[12.04.14]

From the definition of the transfer to Burside's Normal p-Complement Theorem! It was great!

- DV! -

Next time: Free groups (SC), Burnside's problem (LB), and Thompson's groups (RBZ)

Week 15 and Beyond

It's all over... I'm definitely sad, but congratulations on a job very well done! Thanks to you all for a great class. I enjoyed every minute of it! Week 15 and our final exam time were devoted to final presentations. They were excellent!

- #Boss -

- MG! -

- LB! -

- AM! -