Course Information
Meeting times
- Section 01: Tues and Thur from 1:30–2:45 PM (BRH 113)
Book(s)
- Insolvability of the Quintic: An Inquiry-Based Approach to a Second Course in Abstract Algebra by J. Wiscons (the book is free and open source).
Daily Homework
Writing Assignments
Final Project
Course Log
[12.12.24] - Final Exam Period
| What we covered: Worked on our final projects, chatted, ate some snacks, and took our last picture. Thanks for a great year you all! |
 |
Week 15
[12.05.24] - Thursday
| What we covered: We started by outlining the key ideas of Galois theory, many of which we had already observed. We then used this to translate the property of a polynomial $p(x)$ being solvable by radicals over $\mathbb{Q}$ to a condition on the group $\operatorname{Aut}(\mathbb{Q}^{p(x)}/\mathbb{Q})$, namely that the group must be a solvable group. We finished by tying things together to see that the polynomial $x^5 + 5x^4 - 5$ (from the very first problem in the book) is not solvable by radicals over $\mathbb{Q}$. And that’s a wrap…except for the final project. Thanks for a great semester you all! |
[12.03.24] - Tuesday
| What we covered: For the first part of class, we got to see a couple of folks present their solutions to Exam 2—nice job! Then, due to some technical difficulties, the middle portion of class was a very short lecture looking at the way in which complex conjugation can always be viewed as an element of $\operatorname{Aut}(\mathbb{Q}^{p(x)}/\mathbb{Q})$ for any $p(x)\in \mathbb{Q}[x]$. We then finished up with course evals. Next time we’ll wrap up the course and finally see a polynomial that is not solvable by radicals…and get folks prepped for the final project. |
| For next class meeting: HW27 |
Week 14
[11.28.24] - Thursday
| What we covered: Nothing—no class for Fall Break |
[11.26.24] - Tuesday
| What we covered: Most of the day was spent taking a long look at $\operatorname{Aut}(\mathbb{Q}(\sqrt[3]{2},\zeta_3)/\mathbb{Q})$. We began by working out that the group has 6 elements and saw where each map the generators $\sqrt[3]{2}$ and $\zeta_3$. Next we looked at various subfields of $\mathbb{Q}(\sqrt[3]{2},\zeta_3)$ and worked out the corresponding subgroups of $\operatorname{Aut}(\mathbb{Q}(\sqrt[3]{2},\zeta_3)/\mathbb{Q})$. Finally, we rewrote the 6 elements of the group as permutations of the roots of $x^3 - 2$. We finished by returning to $\operatorname{Aut}(\mathbb{Q}(\zeta_5)/\mathbb{Q})$ and writing the elements as permutations of the roots of $x^4+x^3+x^2+x+1$. |
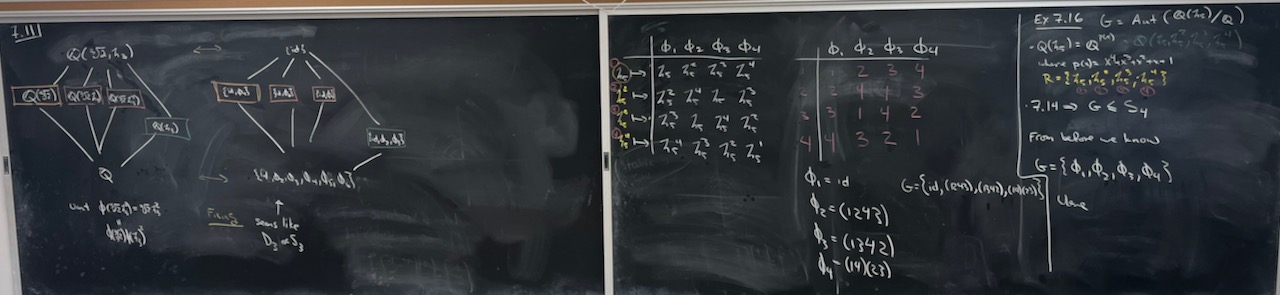 |
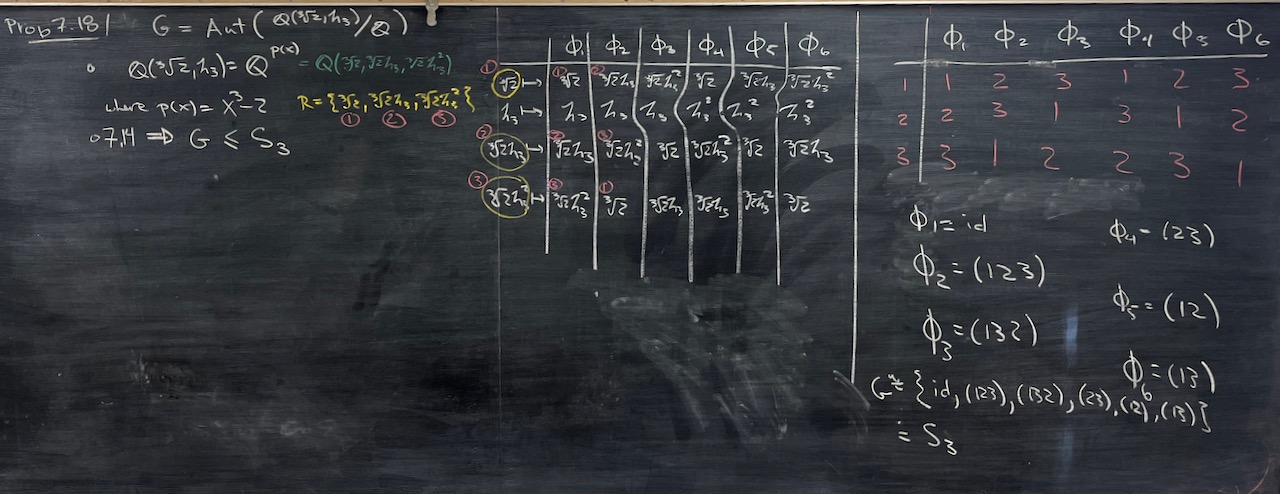 |
| For next class meeting: HW26 |
Week 13
[11.21.24] - Thursday
| What we covered: Began with a couple problems from last time that explored $\operatorname{Aut}(\mathbb{Q}(\sqrt{2},i)/\mathbb{Q})$. The first problem showed that $\operatorname{Aut}(\mathbb{Q}(\sqrt{2},i)/\mathbb{Q}) \cong V_4$, and the second explicitly connected the subgroups of $V_4$ with subfields of $\mathbb{Q}(\sqrt{2},i)$. Next we started in on Galois extensions, mostly just wrapping our heads around the defintion. We again have a couple problems to pick up with next time, which will look at $\operatorname{Aut}(\mathbb{Q}(\sqrt[3]{2},\zeta_3)/\mathbb{Q})$. |
 |
 |
| Due next class meeting: HW25 |
[11.19.24] - Tuesday
| What we covered: Started with a few problems from last time looking at isomorphisms and non-isomorphisms between fields of the form $\mathbb{Q}(\alpha)$ and how these are controlled by the minimal polynomial of $\alpha$. We then sharpened our focus to automorphism of fields and saw (among other things) that $\operatorname{Aut}(\mathbb{Q}(\zeta_5)/\mathbb{Q})$ is a group isomorphic to $\mathbb{Z}_4$. Next time we’ll pick up with the final two problems, which explore $\operatorname{Aut}(\mathbb{Q}(\sqrt{2},i)/\mathbb{Q})$. |
 |
 |
| Due next class meeting: HW24 |
Week 12
[11.14.24] - Thursday
| What we covered: Started with a couple of problems from last time about the degree of extensions and using the multiplicative property. Then we began what will be a long discussion of functions between fields, taking into account that we will want our functions to respect the field structure (addition and multiplication) as well as the linear algebraic structure that comes from having subfields. Ran out of time again so will get to the final three problems next time. |
  |
 |
| Due next class meeting: HW23 |
[11.12.24] - Tuesday
| What we covered: The focus was on computing bases (and degrees) for field extensions. We worked a few examples and started to see the utility of the “multiplicative property” for towers of field extensions. We ran out of time before getting to the final two problems, so we’ll start next time by taking a look at them. |
 |
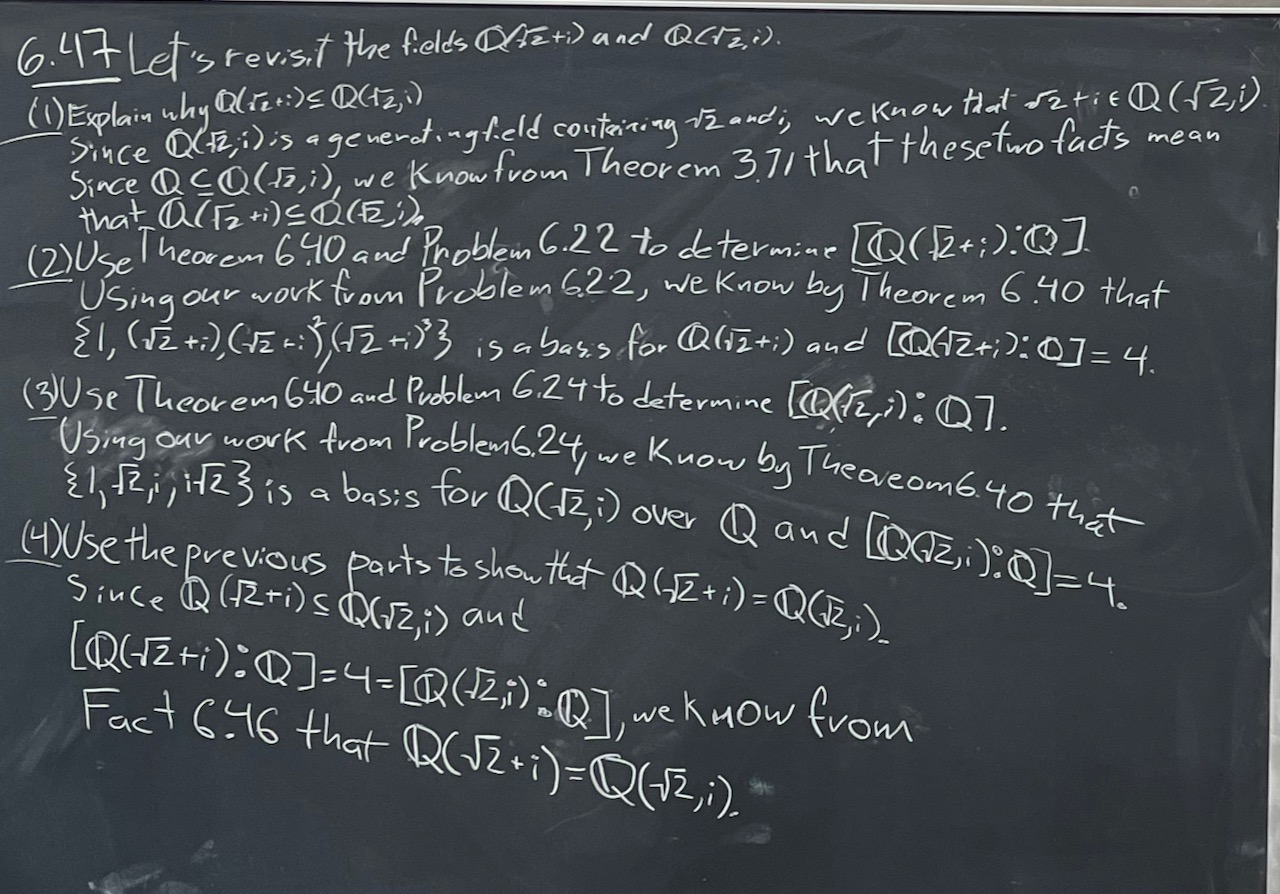 |
| Due next class meeting: HW22 |
Week 11
[11.05.24] - Thursday
| What we covered: There was lots to talk about. We started by checking in about the election to see how folks are doing—thanks for taking part and making space for that. We also talked about a little math. The focus was on using EIC to show polynomials are irreducible over $\mathbb{Q}$. At the end, we also introduced some linear algebra terminology and explored it in the context of $\mathbb{Q}(\alpha)$ for $\alpha$ a root of $x^5+5x^4-5$, ultimately seeing that $\mathbb{Q}(\alpha)$ is $5$-dimensional over $\mathbb{Q}$. But the highlight of the day, was a joke by SB: “why can’t you grow wheat in $\mathbb{Z}_6$?” |
 |
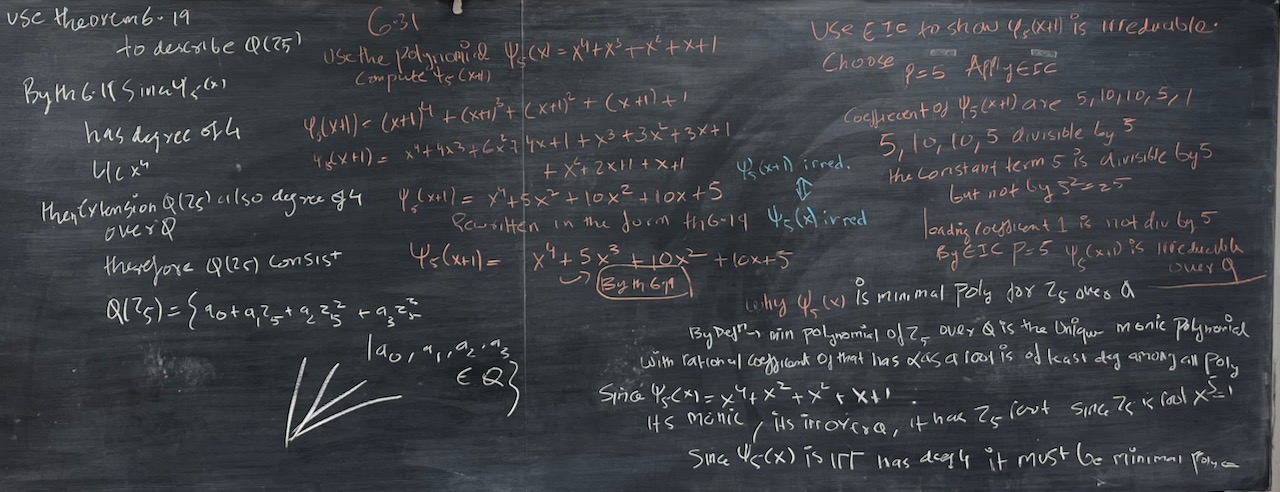 |
| Due next class meeting: HW21 |
[11.05.24] - Tuesday - Election Day
| What we covered: Today we learned how to nicely describe the elements of $F(\alpha)$ once we know the degree of $\alpha$ over $F$. We saw this in action for $\mathbb{Q}(\zeta_3)$, $\mathbb{Q}(\sqrt{2} + i)$, $\mathbb{Q}(\sqrt{2},i)$, and $\mathbb{Z}_3(r)$ with $r$ a root of $x^3-x+1$. We also saw that when multiplying elements of $F(\alpha)$ we can use the minimal polynomial to reduce powers. Up next is another tool for helping us find minimal polynomials. |
 |
 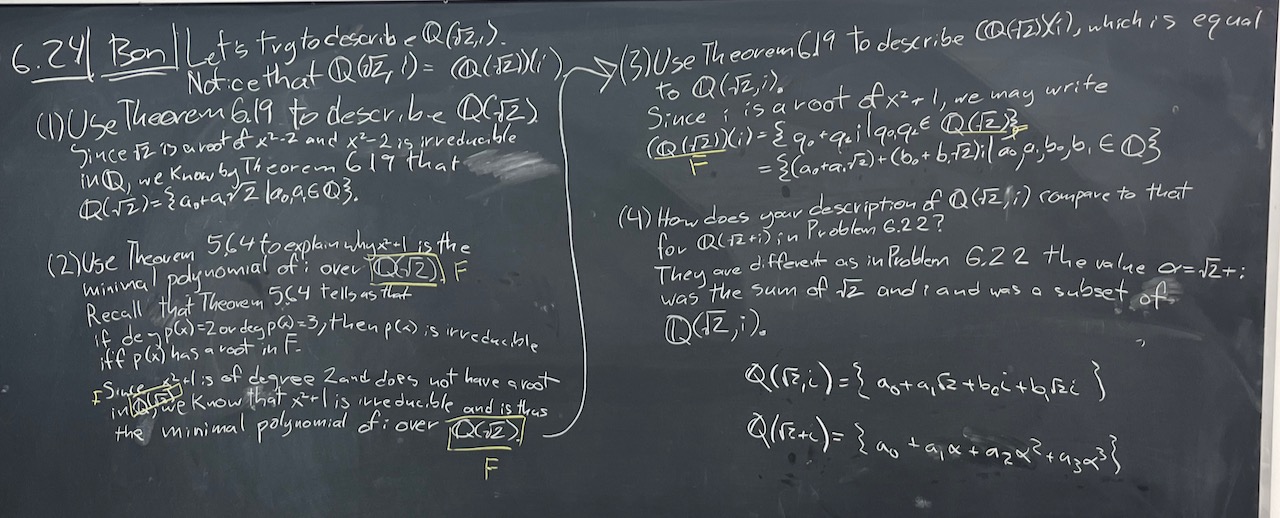 |
| Due next class meeting: HW20 |
Week 10
[10.31.24] - Thursday
| What we covered: The focus of the day was on minimal polynomials over a field: how to find them (in certain cases) and that the polynomial may be different depending on what field we are working over. The final problem got us started on the next bit of theory, which will show how the minimal polynomial for $\alpha$ over $F$ can help us develop a concrete description of the field $F(\alpha)$. |
 |
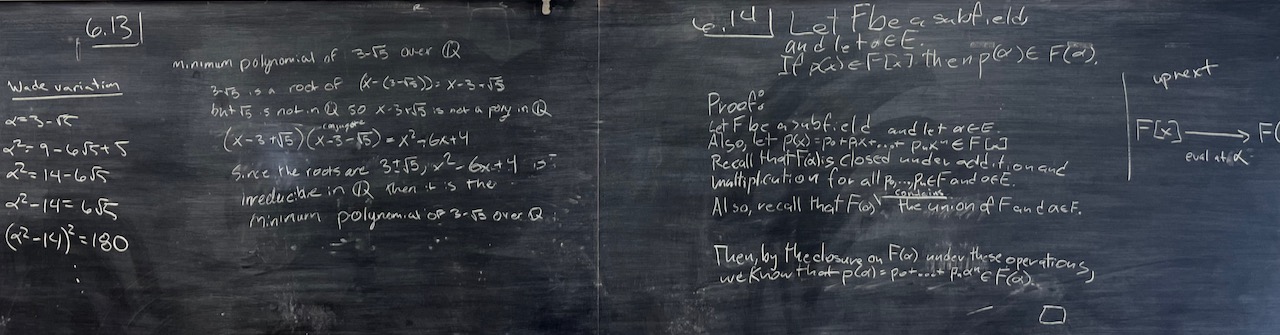 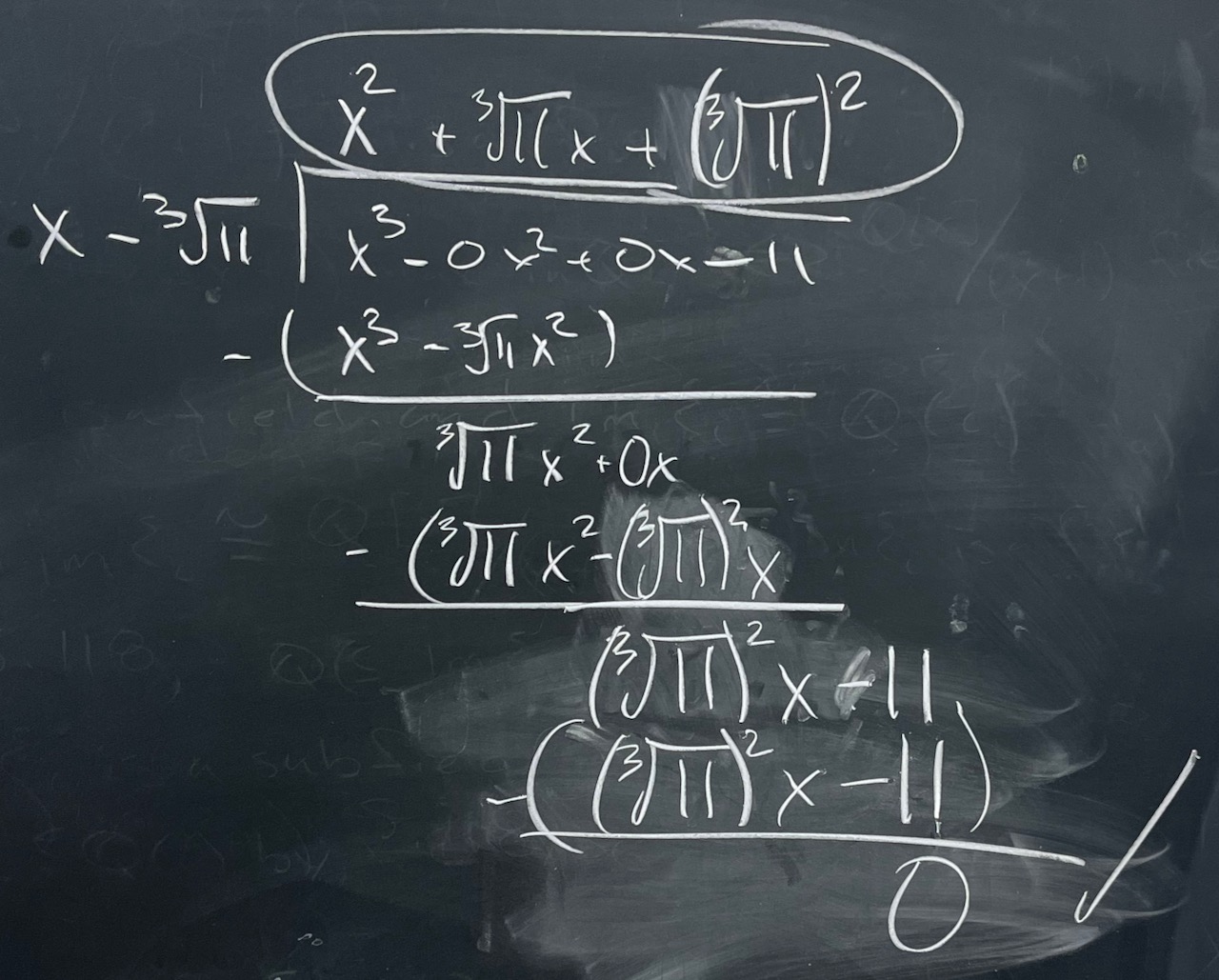 |
| To do: Vote if you’re able to. Also try to work on HW19, but since the election is happening, everyone will get full points on it. |
[10.29.24] - Tuesday
| What we covered: Wrapped up a very lengthy Chapter 5 today! The focus was on kernels, images (and preimages), and the First Isomorphism Theorem, with some applications in examples. We ended with a quick look at the start of Chapter 6 and algebraic elements. |
 |
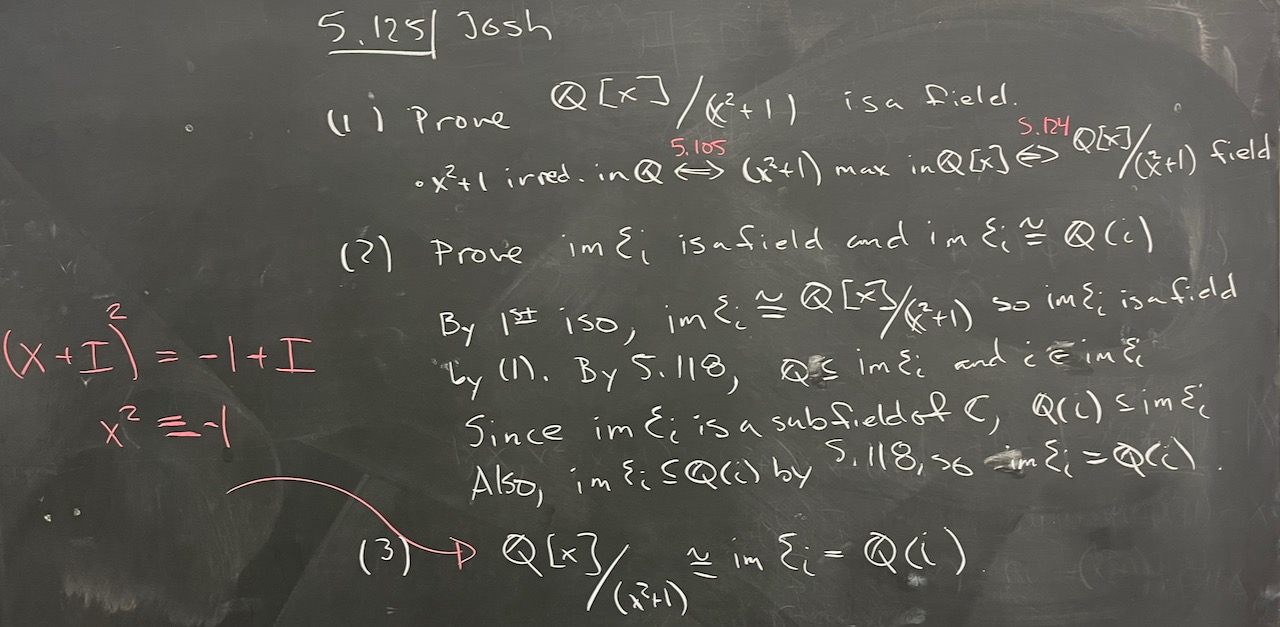  |
| Due next class meeting: HW18 |
Week 9
[10.24.24] - Thursday
| What we covered: lots. Several longer and harder problems today covering ideals (generally and specifically in $F[x]$), homomorphisms (generally and specific examples), and kernels. Great job you all! |
 |
  |
| Due next class meeting: HW17 |
[10.22.24] - Tuesday
| What we covered: The focus of the day was on generating ideals, mostly in commutative rings. In commutative rings with 1, we proved that $(a) = \{ar\mid r\in R\}$ and and that $(a) \subseteq (b)$ iff $b\mid a$. We used this to describe the ideals containing $(60)$ in $\mathbb{Z}$ and the ideals containing $(x^4+x^2)$ in $\mathbb{Q}[x]$. We also saw that all ideals in $\mathbb{Z}$ are principle. We have a couple of lingering problems (5.85 and 5.96) that we’ll start with next time. |
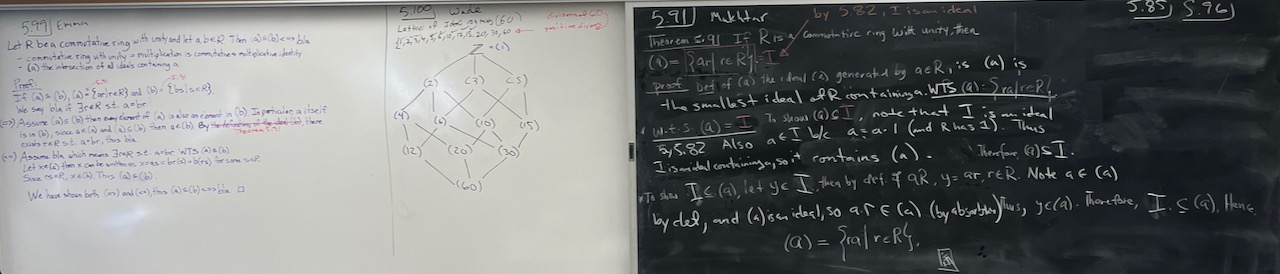 |
  |
| Due next class meeting: HW16 |
Week 8
[10.17.24] - Thursday
| What we covered: Covered a lot of ground today with ideals and quotients, both in specific examples (working in $\mathbb{Q}[x]$ and $\mathbb{Z}$) and abstractly. We’ll continue next time by looking at generating ideals, paralleling how we generated subgroups or subfields before. |
  |
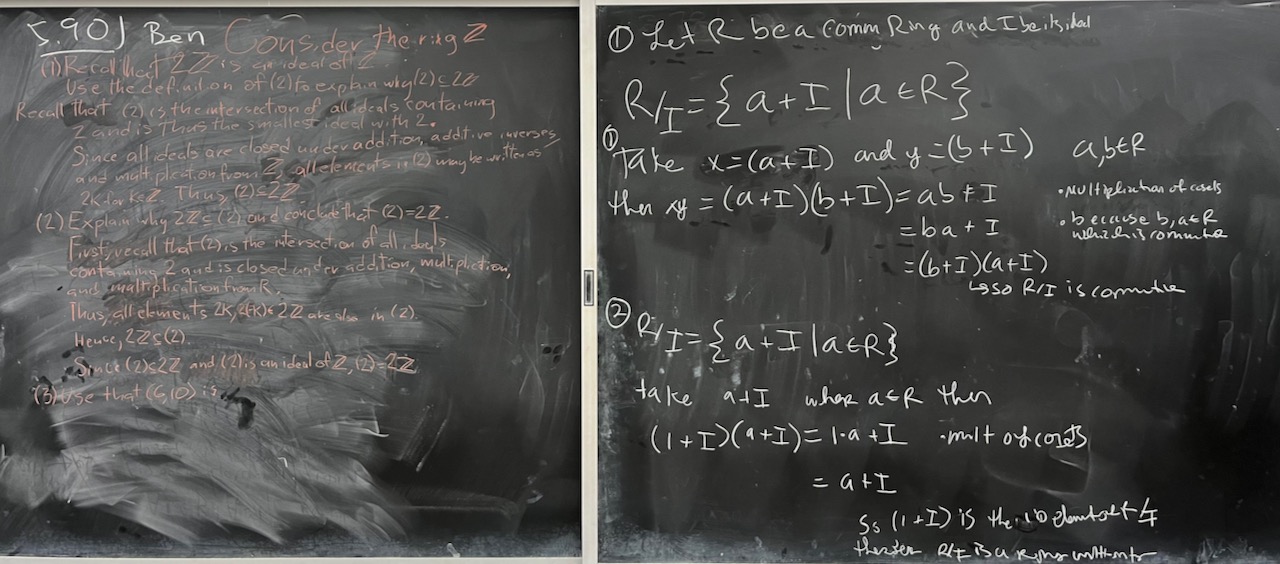 |
| Due next class meeting: HW15 |
[10.15.24] - Tuesday
| What we covered: Started with a little more about irreducibility, and then moved to ideals, cosets, and quotients. We looked at various examples and non-examples of subrings and ideals and took a close look at $\{(x^2+1)p(x)\mid p(x)\in \mathbb{Q}[x]\}$. Unfortunately, there were three problems we didn’t get to today, but we’ll start with them next time. |
 |
 |
 |
| Due next class meeting: HW14 |
Week 7
[10.10.24] - Thursday
| What we covered: First midterm. One down—nice job! |
| Due next class meeting: HW13 |
[10.08.24] - Tuesday
| What we covered: Lectured over the remaining parts of the introduction to polynomial rings and also started discussing subrings, ideals, and quotients. More with ideals and quotients after the exam. |
| Due next class meeting: Nothing. Just study for the first midterm. |
Week 6
[10.03.24] - Thursday
| What we covered: Continued to build the core language and tools for working with polynomials. We started off discussing gcd’s and then at the end moved to the definition and first tests for irreducibility. |
 |
 |
| Look over for next class meeting: HW12 |
[10.01.24] - Tuesday
| What we covered: More with polynomials today with a focus on those with coefficients from a field. We looked at some properties of $F[x]$ (for $F$ a field) such as: the degree of a product is the sum of the degrees, and $(x-c)$ is a factor of $p(x)$ precisely when $c$ is a root of $p(x)$. We also took a look at factoring specific polynomials in $\mathbb{Q}[x]$ and in $\mathbb{Z}_5[x]$. Thanks all for a great day! |
 |
 |
| Due next class meeting: HW11 |
Week 5
[09.26.24] - Thursday
| What we covered: We mainly kept exporing the notions of units and zero divisors in various rings. We took a close look at $\mathbb{Z}_{20}$ and then generalized to $\mathbb{Z}_{n}$. After that we turned our focus to matrix rings, and then we finished with a problem that took us back to polynomials. Lots more with polynomials on the horizon! |
 |
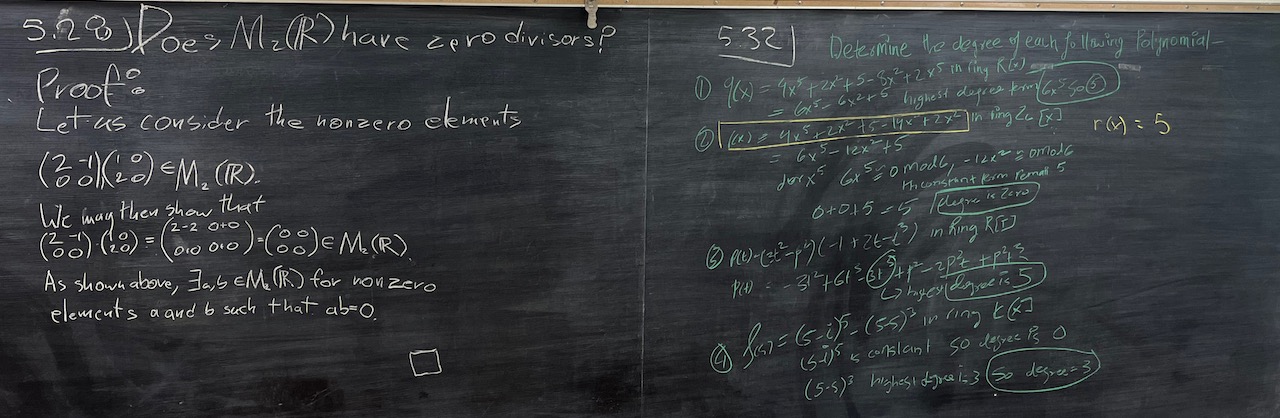 |
| Due next class meeting: HW10 |
[09.24.24] - Tuesday
| What we covered: Started learning about rings today. Spent some time collecting examples of rings with various properties (commutativity, having a unit, being a division ring), and also started discussing special properties of elements such as being a zero divisor or being a unit. We didn’t get to the last two problems, so we’ll start there next time. |
 |
 |
| Due next class meeting: HW09 |
Week 4
[09.19.24] - Thursday
| What we covered: Wrapped up Chapter 4 today! The definitions of ‘radical extensions’ and polynomials being ‘solvable by radicals’ are quite technical, but it seems like folks were pretty onboard by the end of the day. We saw various examples of polynomials that are solvable by radicals like $x^2+3x+1$, $x^3-2$, $x^n-1$, and $x^6-3x^3-1$, and now—for the rest of the course—our goal will be to find one that is not. To do this, we need to explore polynomials in more depth, and this leads us into the topic of rings. Thanks for another fun day! |
 |
 |
| Due next class meeting: HW08 |
[09.17.24] - Tuesday
| What we covered: Continued with generating subfields of $\mathbb{C}$. Last time we saw that $\mathbb{Q}(i) = \mathbb{Q} + \mathbb{Q}i$ and $\mathbb{Q}(\sqrt{5}) = \mathbb{Q} + \mathbb{Q}\sqrt{5}$, but today we showed that $\mathbb{Q}(\alpha) \neq \mathbb{Q} + \mathbb{Q}\alpha$ when $\alpha = \sqrt{2} + i$. (Later on we’ll see how to describe the elements of $\mathbb{Q}(\alpha)$.) We also took a go at organizing different subfields into a common picture: one time we did this via a Venn diagram (which was quite challenging!) and another time we drew a lattice of subfields. After that, we got to work wrapping our head around so-called radical extensions—next time we’ll tie this idea into our formal definition of a polynomial being solvable by radicals. |
  |
 |
| Due next class meeting: HW07 |
Week 3
[09.12.24] - Thursday
| What we covered: Started by seeing another example of a field ($\mathbb{Q} + \mathbb{Q}i$) as well as more nonexamples (like $\mathbb{Q} + \mathbb{Q}\alpha$ where $\alpha = \sqrt{2} + i$). The main topic was generating fields, and we spent most of our time grappling with the definition and then showing that $\mathbb{Q}(i) = \mathbb{Q} + \mathbb{Q}i$ and $\mathbb{Q}(\sqrt{5}) = \mathbb{Q} + \mathbb{Q}\sqrt{5}$. Generating structures is always a challenging topic at first, but you all were asking great questions and seemed to be making sense of things by the end of class. Nice job! |
 |
 |
| Due next class meeting: HW06 |
[09.10.24] - Tuesday
| What we covered: Saw various examples of fields today (like $\mathbb{Q} + \mathbb{Q}\sqrt{5}$, the finite fields $\mathbb{F}_3$ and $\mathbb{F}_4$, and $\mathbb{Z}_p$ with $p$ prime) as well as some nonexamples. We also started proving some basic properties of fields. So sorry I had to miss the first 15 minutes of class—thanks for making it happen without me! |
 |
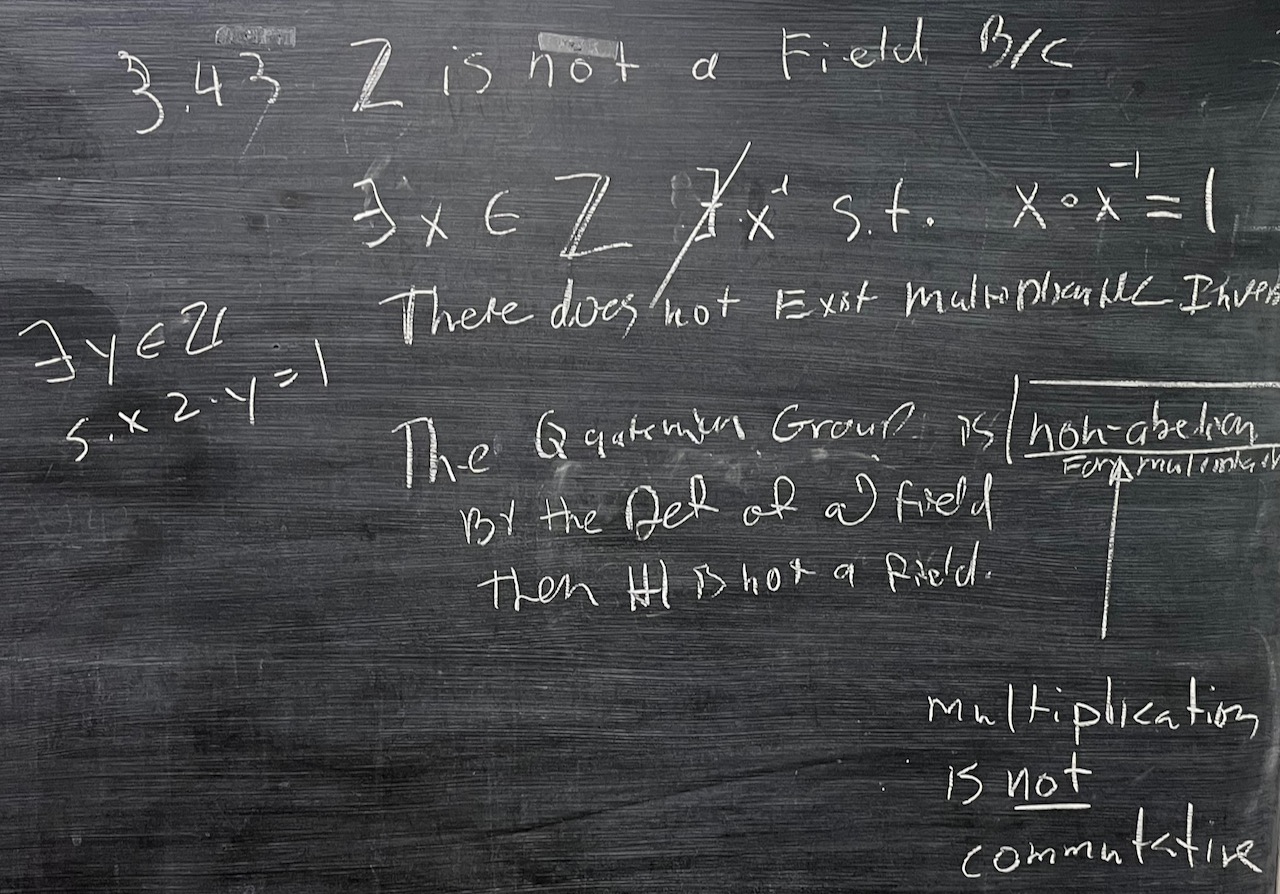  |
 |
| Due next class meeting: HW05 |
Week 2
[09.05.24] - Thursday
| What we covered: We started by wrapping up roots of unity and finding all solutions to $x^n = a$ in the complex numbers. We then spent a little time on the quaternions and finished with a problem leading the way into our upcoming discusion of fields. |
 |
 |
 |
| Due next class meeting: HW04 |
[09.03.24] - Tuesday
| What we covered: Continued to explore basic facts about complex numbers (like de Moivre’s formula), and then started in on roots of unity. Unfortunately we didn’t get to talk about the last two problems, but we’ll cover then next time. |
 |
  |
| Due next class meeting: HW03 |
Week 1
[08.29.24] - Thursday
| What we covered: Spent a little more time framing the course and talking about formulas for roots of polynomials; a key thing was to start exploring the idea of a polynomial being ‘solvable by radicals’. After that, we started in on complex numbers with an initial focus on ways to represent and manipulate them. Many thanks to you all—presenters and audience members alike—for a great day! Hope you get to enjoy the long weekend! |
 |
 |
 |
| Due next class meeting: HW02 |
[08.27.24] - Tuesday
| What we covered: First day of class! After introductions and discussing the syllabus, we got started in on some math. We looked at finding roots of polynomials, which then led to questions about possible analogues of the quadratic equation. This is main thread of the course, and we’ll spend the semester answering this! Looking forward to Thursday! |
 |
| Due next class meeting (08/29): Please work on: HW01. You will not be graded on this first assignment, but we will talk about it in class. |